格子类的问题总结

标签：+=   关系   ring   com   clu   tps   cpp   blog   直接   

前言

最近或者以前做的一些题目中，总是有一些格子类的题目，大致就是给一个\(N×M\)的方格，然后让你求一些东西，我目前见到的解题方法有大致三种：

• 建图
• DP
• 思维

简单总结一下，有什么漏洞欢迎指出。
首先是和图有关系的，当然那种裸的Floyd就不看了。

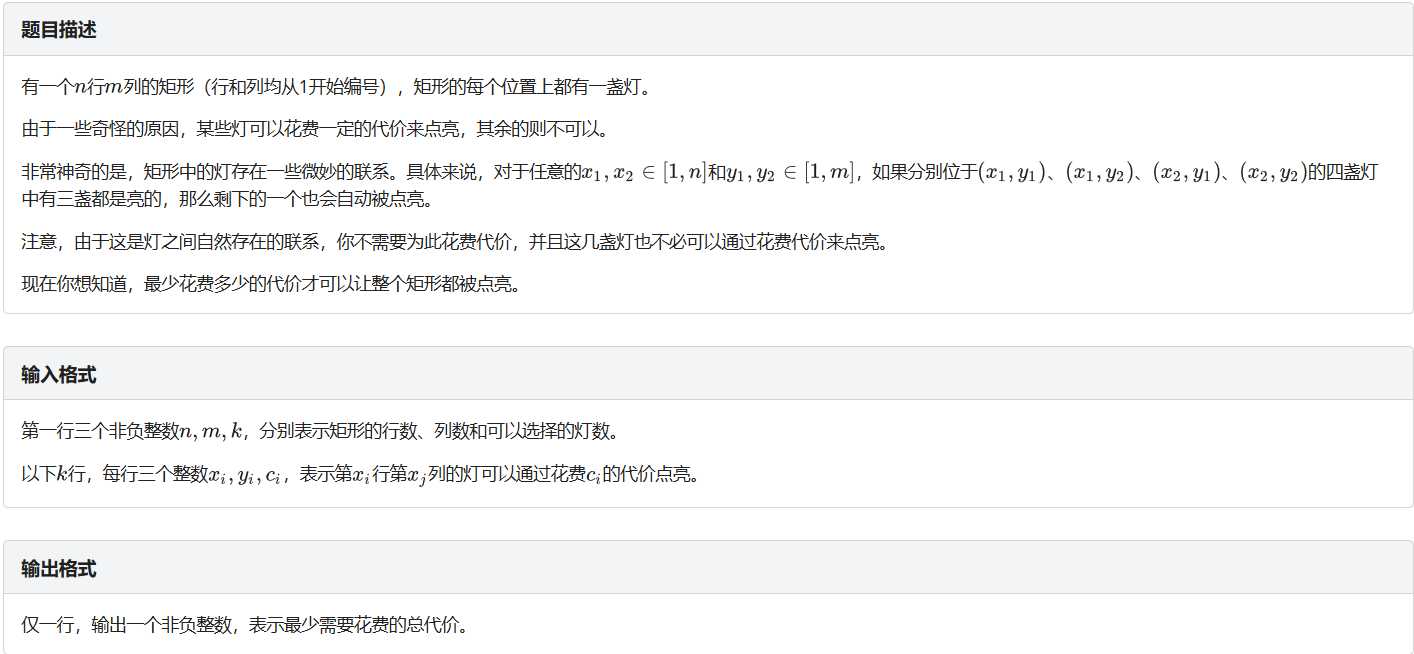
这个东西第一眼看见没什么思路，但是要深挖一下它的内涵。
假设有两行两列的四个交点为\(x,y,w,z\)，只要其中的任意三点被点亮，剩下的那个就亮了。
换句话说，我们只要把这四个点之间连上边，只要任意三个点联通，这四个点就会联通，于是这就是一个藏得很深的最小生成树了。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=3e6+10;
struct Edge{
	long long to,from,val;
	Edge(){to=from=val=0;}
	bool operator < (const Edge &A)const {
		return val<A.val;
	}
}e[3*N];
long long len=0,m,n,k,fa[N];
void Ins(long long a,long long b,long long c){
	e[++len].to=b;e[len].from=a;e[len].val=c;
}
long long Find(long long x){
	return fa[x]==x?x:(fa[x]=Find(fa[x]));
}
void Mer(long long a,long long b){
	fa[Find(a)]=Find(b);
}
long long Kru(){
	sort(e+1,e+len+1);
	long long ans=0;long long cnt=1;
	for(long long x=1;x<=len;x++){
		long long u=e[x].from,v=e[x].to;
		if(Find(u)!=Find(v)){
			Mer(u,v);
			ans+=e[x].val;
			if(++cnt==n+m){
				return ans;
			}
		}
	}
	return -1;
}
int main(){
//	freopen("a.txt","r",stdin);
	scanf("%d%d%d",&n,&m,&k);
	for(long long i=1;i<=m+n+1;i++)
		fa[i]=i;
	for(long long i=1;i<=k;i++){
		long long a,b,c;
		scanf("%lld%lld%lld",&a,&b,&c);
		b+=n;Ins(a,b,c);Ins(b,a,c);
	}
	printf("%lld",Kru());
	return 0;
}

UVa11383
这道题给的题意就是给了一个矩阵，让你去赋值。
建图然后跑KM算法就行。
题解在这里
然后就是用DP的解法了，当给的矩阵很小并且限制条件十分复杂的时候，可以考虑用状压DP
互不侵犯
范围这么小，直接状压~
但是这里要注意提前预处理出可行状态，排除掉如111111这种的完全不可行的状态。

格子类的问题总结

标签：+=   关系   ring   com   clu   tps   cpp   blog   直接   

原文地址：https://www.cnblogs.com/anyixing-fly/p/12951208.html