标签:等于 编译 def node 路径 说明 平衡 否则 保存
void PreOrder(BiTree T) {//先序遍历二叉树 if(T!=NULL)//若树非空 { cout<<T->data;//访问根节点 PreOrder(T->lchild);//先序遍历左子树 PreOrder(T->rchild);//先序遍历右子树 } }
void InOrder(BiTree T) {//中序遍历二叉树(递归) if(T!=NULL)//若树非空 { InOrder(T->lchild);//中序遍历左子树 cout<<T->data;//访问根节点 InOrder(T->rchild);//中序遍历右子树 } }
void InOrder2(BiTree T) {//中序遍历非递归算法 InitStack(S); BiTree p=T; while(p||IsEmpty(S)) { if(p) { Push(S,p); p=p->lchild; } else { Pop(S,p); visit(p); p=p->rchild; } } }
void PostOrder(BiTree T) {//后序遍历二叉树 if(T!=NULL)//若树非空 { PostOrder(T->lchild);//后序遍历左子树 PostOrder(T->rchild);//后序遍历右子树
cout<<T->data;//访问根节点 } }
void LevelOrder(Tree T) { queue<int> Q;//队列 Q.push(T.root);//根结点入队 int k; bool flag=false; while(!Q.empty()) { k = Q.front();//获取队头元素 Q.pop();//队头元素出队 if(T.data[k].lch==-1 && T.data[k].rch==-1) {//叶子结点 if(flag==false) { cout<<k;//输出叶子结点的编号 flag=true; } else { cout<<" "<<k; } } else {//不是叶子结点 if(T.data[k].lch!=-1) Q.push(T.data[k].lch); if(T.data[k].rch!=-1) Q.push(T.data[k].rch); } } }
————————————————————
5.11课堂笔记
第4章PTA实践:
两个整数集合(集合内无重复元素),集合元素个数<=100000,求两集合交集,并按非降序输出
1)直接遍历 O(m*n)+Q(排序)
2)先排序再合并 O(nlogn)+O(m+n) stl:sort函数!!!
5.9PTA个人赛:
测试点3:5000 连续相同编号输入积分,遇到不同编号时break
测试点4:10000
1)将数组和长度隔开成为两个变量
2)将数组和长度打包为一个结构体
SqList L;
cin>>L.length;
L.data[3].id/.money
分析顺序表、结构体、数组之间的关系:
顺序表(结构体(数组))
typedef struct{
string id;
int money;
}node;
typedef struct{
node data[MAXSIZE];
int length;
}SqList;
SPOC substr讨论
string可以视作C风格的字符型数组
string t;
空串 t[0] t[1] 非法访问内存
string t="1234";//合法:t[0]~t[3]
char *p="123456";//在常量区写入123456,将该字符串的首地址返回给p
char s[]="123456";//在栈空间中给s分配一个空间,大小为7个字符(加上\0)
p[0] =‘0‘;//在常量区存储,不能修改(编译正确,运行时非法)
s[0] = ‘0‘;//可以修改
char *t = new char[10];//在堆空间开辟是个字符大小的空间,将首地址赋值给t,合法t[0]~t[9]
t = "123456";//在常量区开辟空间写入该字符串,再将首地址返回给t;原来通过t申请的空间没有释放,产生内存泄漏
5.11课堂提问
1.一棵有201个结点的完全二叉树,其中叶子结点的个数是?
对任何一棵二叉树T, 如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1
如果该完全二叉树存在一个度为1的结点,那总数一定为偶数,故不存在度为1的结点
n2=(201-1)/2 n0=n2+1=101
2。一个具有258个结点的二叉树的高h为?
本题未说明是否为完全二叉树,最矮情况下高度=(log2 258)+1=9,最高情况下为单支树,高度为258
3.深度为h的满m叉树的第k层有多少个结点?(1<=k<=h)
二叉树第i层上至多有2^(i-1)个结点,故结点数为 m^(k-1)
5.11SPOC讨论
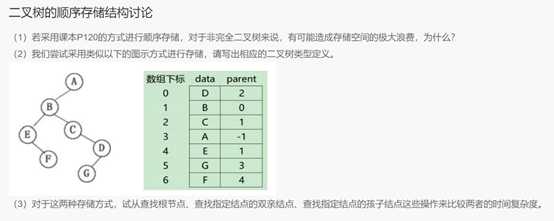
二叉树的顺序存储结构:
1)若采用课本P120的方式进行顺序存储,对于非完全二叉树来说,有可能造成存储空间的极大浪费,为什么?
因为用该方式存储非完全二叉树时,需要在其对应完全二叉树的位置空缺时进行补齐,会对空间造成浪费
————————————————————
5.12课堂提问
1、若有一二叉树的总结点数为98,只有一个儿子的结点数为48,则该树的叶结点数是多少?
不存在,n=98,n1=48,所以n0+n2=50,又因为n0=n2+1 为奇数,故不存在
2、在一棵度为3的树T中,若有10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶子结点个数为?
22个,n3=10,n2=1,n1=10,分支总数=10*3+1*2+10*1=42
而在一棵树中只有根结点没有分支指向,所以结点总数=分支总数+1,n=43
n0=43-10-1-10=22
————————————————————
5.18课堂笔记
讨论疑问:
1)

将二叉树根结点下标与nodes打包,可以通过根节点下表找双亲
利用Node *nodes;在初始化时申请空间,避免数组大小不足或浪费
2)
typedef struct
{
char data;
int parent;
}BiTNode;
int n;//需要包在函数内出现
cin>>n;
BiTNode *BiTree new BiTNode[n];//在堆空间存储
int n; cin>>n; int a[n];//常量区存储 C可以 C++不行
3)

Parent跟数组打包在一起,指向不明

名字查找 下标查找
O(n) O(n)
O(1) O(1)
O(n)……
找双亲的下标公式
i/2(向下取整)
课堂问题

如果T为空,直接退出函数

Fun函数:
利用STL中的queue模板
层次遍历:
一层一层向下遍历,遍历当前结点时,同时保存孩子结点
先进先出,利用队列
q.push(T);//T结点入队相当于地址入队
BiTNode *p;//定义与q相同类型的p
当q不为空时
P=q.front();//q队头元素赋值给p
q.pop();//弹出队头元素
标签:等于 编译 def node 路径 说明 平衡 否则 保存
原文地址:https://www.cnblogs.com/cmlearning/p/12886286.html