标签:style blog http io color sp for div on
题目:和上一题类似,就是这个时候给定了矩阵包含0和1,1代表不能从这里走。我的想法其实很明确,还是用动态规划,只是碰到壁垒的时候要进行考虑。还有初始化很重要。
因为1本来是要用来代表在这里出发到终点有一种可能的,所以壁垒的1要用其他代替,我用-1代表是壁垒。
如果给定的数组第一个数就是1,那永远都出发不了,那就是返回0种可能。如果有且仅有一个数那就返回1。之后考虑在不止一个数的情况。如图:
假设原来的数组为:
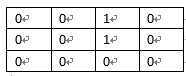
那么初始化后应该是:
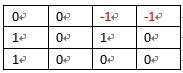
之后就判断i和j都从1开始,并且是从左边一个数和上一个数的和,但是有三种可能
1.如果本身就是1,那么直接赋值-1,因为不能从这里过
2.如果左边是-1,那么就把当前的赋值为上面的
3.如果上面的是-1,那么就把当前的赋值为左边的
如上例子应该为:
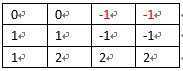
代码如下:
class Solution { public: int uniquePathsWithObstacles(vector<vector<int> > &obstacleGrid) { // if(obstacleGrid.size() < 1) return 1; if(obstacleGrid[0][0] == 1) return 0; if(obstacleGrid.size() == 1 && obstacleGrid[0].size()==1) return 1; int m = obstacleGrid.size(), n = obstacleGrid[0].size(); int i = 1, j = 1; while(j<n && obstacleGrid[0][j] != 1) obstacleGrid[0][j++]=1; while(j<n) obstacleGrid[0][j++] = -1; while(i<m && obstacleGrid[i][0] != 1) obstacleGrid[i++][0]=1; while(i<m) obstacleGrid[i++][0] = -1; for (i = 1; i < m; ++i) for (j = 1; j < n; ++j) { if (obstacleGrid[i][j] == 1) { obstacleGrid[i][j] = -1; continue; } int left = obstacleGrid[i][j-1], up = obstacleGrid[i-1][j]; if (left != -1 && up != -1) obstacleGrid[i][j] = left + up; else if (left == -1) obstacleGrid[i][j] = up; else obstacleGrid[i][j] = left; } if (obstacleGrid[m-1][n-1] == -1) return 0; return obstacleGrid[m-1][n-1]; } };
标签:style blog http io color sp for div on
原文地址:http://www.cnblogs.com/higerzhang/p/4082613.html