标签:关于 details 基础 inf 区分 向量 jpg 最小值 str
2020-05-25
这是我在CSDN上看到大佬博主写的,原文链接:https://blog.csdn.net/Candle_light/article/details/84759089
可行解,最优解,基,基向量,非基向量,基变量,非基变量等
已知标准型为:
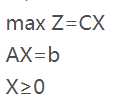
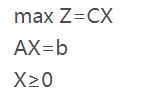
可行解: 满足约束条件,AX=b ,X>=0 的解叫做线性规划问题的可行解。
最优解:使目标函数Z=CX达到最大值的可行解(上面的标准型是到最大值,还有的是求最小值,要求不同,注意区分)。
基,基向量,非基向量,基变量,非基变量

基本解(又叫做基解,基础解):若在约束方程组系数矩阵中找到一个基,令其非基变量为零,再求解该m元线性方程组可得到唯一解,该解称之为线性规划的基本解。基解,基可行解,可行基

需要注意的问题是:基本解不一定是可行解,非负的基解才是可行解。
奇异矩阵和非奇异矩阵:奇异矩阵和非奇异矩阵都是方阵(行列数相同),如果矩阵A对应的行列式为0,那么这个矩阵A就是奇异矩阵,如果A对应的行列式部位0,那这时A就是非奇异矩阵。
关于奇异阵,非奇异阵,可逆和线性方程组的解的关系,总结一下就是:
(1)A为非奇异矩阵,则|A| ≠ 0 → A是可逆矩阵 → AX=0只有唯一零解 或 AX=b有唯一解
(2)A为奇异矩阵,则|A| = 0 → A是不可逆矩阵 → AX=0有非零解 或 AX=b有无穷解或者无解
最优解的特点:

作业题


标签:关于 details 基础 inf 区分 向量 jpg 最小值 str
原文地址:https://www.cnblogs.com/ctt521/p/12955934.html