标签:大智慧 因变量 无法 回归 看不见 ima 市场 负数 ==
回归分析给不了因果因此,用回归去研究相关关系
Y是什么?俗称因变量。取义,因为别人的改变,而改变的变量。在实际应用中,Y刻画的是业务的核心诉求,是科学研究的关键问题。[王汉生](https://mp.weixin.qq.com/s?__biz=MzA5MjEyMTYwMg==&mid=2650236514&idx=1&sn=ad7b2be0004c5eb98c7e2ca89cd50bba&scene=21#wechat_redirect
例1,对于征信而言,业务的核心指标是什么?就是隔壁老王找我借钱,最后他呢,是还呢还是不还?如果还,我们定义老王的Y=0,这说明老王是好人。如果不还,我们定义老王的Y=1,这说明老王是坏蛋。这就是征信的核心业务诉求,这就是因变量Y。在这个情况下,因变量是一个取值为0-1的变量,俗称0-1变量。这是例1。
同理在连续问题中,y是一系列连续的取值
X是什么?X就是用来解释Y的相关变量。可以是一个,也可以是很多个。我们通常把X称作:解释性变量。而回归分析的任务就是,通过研究X和Y的相关关系,尝试去解释Y的形成机制,进而达到通过X去预测Y的目的。[王汉生](https://mp.weixin.qq.com/s?__biz=MzA5MjEyMTYwMg==&mid=2650236514&idx=1&sn=ad7b2be0004c5eb98c7e2ca89cd50bba&scene=21#wechat_redirect)
举个作者提到的例子
对于征信而言,我们已经讨论过了,Y=0或者1,表示隔壁老王是否还钱,这是我业务的核心指标。当老王找我借钱的那个时刻,我并不知道老王是否将来会还钱,也就是说呀,我不知道老王的Y呢。怎么办?我只能通过当时能够看得到的,关于老王的X,去预测老王的Y。这种预测是否会100%的准确?答:基本上不可能。但是,希望能够做的比拍脑袋更准。这是非常有可能的。为此,我们需要寻找优质的X。寻找过程如下:
假设,老王想找我借1万块钱现金,我得想想,他会还吗?此时,如果我知道他家有一个大大的house,价值几千万,我大概就不怎么担心你不还钱了。因为你不还钱,我就去你家收房子,这可比1万块钱值得多了去了。这说明什么?这说明充足的实物资产,尤其是可以抵押的实物资产,是有可能极大的影响一个人的还钱行为。如果这个业务分析是正确的,那么我们可以定义很多X,用于描述老王的财产情况。例如:X1表示你是否有房本儿;X2表示你是否有车本儿;X3表示你是否有黄金首饰可以抵押,等等。类似的,我们可以定很多X,都围绕着老王的实物资产打转。
除了实物资产以外,老王还有哪些特征,有可能影响他的还钱行为呢?我们再想,如果老王工资月入十万,那还款一万块钱,不是小菜一碟吗?相反,如果老王月入一千,估计吃饭都有问题,哪来的钱还?这说明什么?这说明老王的收入,可能同他的还款行为有相关关系。那么,我们是否可以构造一系列的X,用于描述老王的收入情况?例如,我们可以重新定义X1是老王的工资收入;X2是老王的股票收入;X3是老王太太的收入(老王没钱,太太有钱也可以的),等等。于是,朴素的业务直觉,又引导我们产生了一堆新的X变量,他们都围绕着老王的收入打转。
除了实物资产、收入以外,老王还有啥值钱的呀?有啊,老王有自己在社交圈中的尊严。就像电影老炮里面的顽主六爷那样,面子老大了,不会为了万把块钱,去赖帐,然后让街坊邻居、同事朋友都笑话,丢不起那人。如果,老王是一个这样的人,那他的还款意愿会很强烈。这个朴素的业务直觉说明什么?说明一个人的社交圈,他的社交资产是可以影响到他的还款行为的。如果这个直觉是对的,那么哪些指标会刻画一个人的社交资产呢?为此又可以头脑风暴一把,产生好多有趣的变量出来。例如,这一次我们定义X1是老王的微信好友个数;X2是微博好友个数;X3是电话本上的好友个数;X4是QQ好友个数,等等。我们可以生成一堆新的X变量,他们都围绕着老王的社交资产打转。
以上就是一些关于X的讨论。
因此需要验证的几个问题:
回归分析要去识别并判断:哪些X变量是同Y真的相关,哪些不是。
去除了那些同Y不相关的X变量,那么剩下的,就都是重要的、有用的X变量了。接下来回归分析要回答的问题是:这些有用的X变量同Y的相关关系是正的呢,还是负的?
在确定了重要的X变量的前提下,我们还想赋予不同X不同的权重,也就是不同的回归系数,进而我们可以知道不同变量之间的相对重要性。
第一、识别重要变量;
第二、判断相关性的方向;
第三、要估计权重(回归系数)。
这些个回归的定义,仔细看就是根据因变量的类型
普通线性回归的主要特征就是:它的因变量必须是连续型数据。什么是连续型数据呀?简单通俗的讲,就是得是连续的。例如:身高、体重、价格、温度都是典型的连续型数据。但是,在实际工作中,由于所有的计算机,实际上都只能存储有限位有效数字,因此,在真实的数据江湖里,不存在严格的连续数据,只有近似的。回归五式
举例子:客户终身价值。
这里的因变量Y是一个目标客户,从现在开始,到未来无限远时间,所能够给企业创造的收入,经过一定的利率折现到现在的价值。如果我们能够建立Y和一系列X的相关关系,例如X可以是这些消费者的人口统计特征以及过去的消费记录,我就可以通过X去预测Y。这样可以帮助我们识别潜在的高价值客户。回归五式
简单总结一下:线性回归模型,就是一个数学上可以表达为: Y = beta0 + beta1X1 + beta2X2 + ... + betap*Xp + epsilon的模型。其分析主要围绕着各个beta系数,以及epsilon的方差展开。线性回归
斜率和截距这个比较好理解,主要还是理解一下eposion
这个模型还涉及到一个看不见摸不着的epsilon。
请大家千万不要小看它。这可是统计学的大智慧!没有epsilon的存在,就变成Y=beta0+beta1*X,这是什么?这是一个线性代数问题,跟统计学没嘛关系。但是,一旦有了epsilon,这就是一个标准的线性回归模型。
大家可能会问,反正epsilon也是看不见,摸不着的。我们能对它做什么分析呢?它能!我们主要想分析一下这个epsilon的变异性(也就是说是它的方差有多大)。如果epsilon的方差很小,恨不得就是0,那么原来的线性回归问题就退化为一个线性方程问题。
这时候啊,我们能够基于X,对Y做出极其精准的预测。相反,如果epsilon的方差很大,大得不得了。这说明什么?这说明Y主要是被epsilon驱动的,而X的影响力非常微弱。
数学上可以严格证明,Y的方差完全由X的方差和epsilon的方差所决定。因此,了解epsilon方差的大小,可以帮助我们了解,在多大程度上,Y可以被X准确预测。而这个预测的精确程度,是可以通过一个叫做判决系数(也就是R.Squared)来做一个粗糙的度量。
量化一个回归模型的预测能力(或者拟合优度,这是一个硬币的两面)。这个问题的极致就是:如果我给你无穷多的样本,以至于能够完全准确地知道β值,您能预测(或者拟合)多好?这个“多好”,能否用一个介乎0%到100%数字刻画?这就是熊大版本R.Squared的朴素目的。

大家看,这就是熊大脑袋中的R.Squared。我应该不是第一个如此定义R.Squared的人。其核心是:把因变量Y的信息拆分成两部分,一部分是可以被X解释的(即:X‘β),而另外一部分是X无法解释的(即:ε)。然后再研究这两部分信息中,第一部分(可以被X解释的部分)占比如何。这就是熊大牌R.Squared最原始的定义。怎么样,这个好懂吗?
如果这个基本理念清楚了,接下来需要回答的问题是:怎么测量信息?唉,这又是一个八百年扯不清楚的问题,估计没有最优解。但是,在线性回归的框架下,大家发现方差也许是一个可以接受的选择。如果一个变量方差为0,这说明什么?这说明它是一个常数,因此无法刻画不同样本之间的区别,所以它的信息量是0。嗯,这个似乎有道理。两个不同的变量,在单位相同可比的前提下,方差大的变量,自然更能刻画不同样本之间的差异,所以信息量似乎更大一些。怎么样,这个能接受吗?
好,如果我们同意用方差来刻画信息,那么,刚才定义的R.Squared就可以更加具体一点,变成
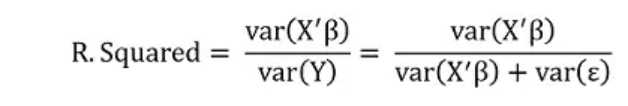
如果R.Squared=0,这说明var(X‘β)=0。一般情况下这说明β=0,因此解释性变量X同因变量Y没有毛关系。如果R.Squared=100%,这说明var(ε)=0。这说明ε=0,因此解释性变量X同因变量Y是确定性的线性关系(以概率为1)。这说明什么?这说明如此定义的R.Squared满足我们最初的设计预期,能够粗糙地量化一个线性模型的预测能力(或者拟合优度),非常棒!
因变量是0-1型数据。什么是“0-1型数据”?0-1型数据就是说呀,这个数据只可能有两个取值。
例如:性别,只有“男”、“女”两个取值;消费者的购买决策,只有“买”或者“不买”两个取值;病人的癌症诊断,只有“得癌症”或者“不得癌症”两个取值。类似地,大家可以给出很多0-1型数据的例子来。
碰到这种数据挑战的时候,线性回归就不好使了。你需要的是回归分析第2式:0-1回归。0-1回归主要砍的就是0-1型因变量的问题。0-1型的因变量又包含了很多很多的招数,我个人认为,其实大同小异,最常见的有两招就可以了。一招是:逻辑回归,也叫做Logistic Regression;另外一招是:Probit Regression。
具体想学的同学,大家可以去查“广义线性模型”相关的武林秘籍,我就不再这里赘述了。我主要想跟大家分享的是:“0-1回归”是一个非常重要的回归模型,你要不会这招,休想行走数据江湖,永远不可能到达价值的彼岸。
大家都喜欢网上购物,什么淘宝、京东、天猫啥的。每一次登陆进自己的账户,我们看到了什么?是不是总能看到一些被推荐的商品,“猜你喜欢”,对不?这些商品是怎么被推荐出来的?这个背后啊,也是一个0-1回归的问题。
举个例子,咱先找一堆X1描述消费者的特征(什么性别啦、年龄啦、购物习惯啦等等),然后咱们再找一堆的X2描述商品特征(什么品类呀、价格呀、品牌呀、型号呀等等)。咱把这两堆X放在一起,问一个问题:说您会买吗?Y=0表示不会,Y=1表示会。这就是一个标准的0-1回归问题了。
有了这个模型,我们可以知道:对于什么样的消费者,推荐什么样的商品,会产生什么样的购买概率。然后在所有的待选商品中,挑选概率最大的(例如5个),呈现在您的眼前。这就成就了个性化推荐。
有人说了:“王老师,您说的不对,我们用的模型可不是逻辑回归那么简单,老复杂了。”这个木有问题,真正的工程实践,所用的模型,有可能更简单,也有可能更复杂。但是,都逃离不了0-1回归的本质所在。
其实是事情发生的可能性==事情发生的概率
要把一个“0-1型”的因变量数据变成一个连续型的“可能性”的问题,依赖于人们对“可能性”度量手段的不同,可能有不同的“0-1回归”的模型,而逻辑回归就是其中最常见的一种。
就是因变量是定序数据的回归分析。那么,什么又是定序数据呢?定序数据就是关乎顺序的数据,但是又没有具体的数值意义。
考虑一个特别常见的例子。例如,咱公司出一款新的矿泉水,叫做“狗熊山泉,有点不甜”。我想知道消费者对它的喜好程度。因此啊,我决定请人来品尝一下,然后呢,根据他的喜好程度,给出一个打分。1表示非常不喜欢,2表示有点不喜欢,3表示一般般,4表示有点喜欢,5表示非常喜欢。这就是我关心的因变量。
这种数据常见吗?非常常见!有什么特点?
第一、它没有数值意义,不能做任何代数运算。例如,您不能做加法。我不能说:1(很不喜欢)加上一个2(有点不喜欢)居然等于了3(表示一般般)。这显然不对。这就是该数据的第一个特点,没有具体的数值意义。
第二,这个数据的第二个特点是它的顺序很重要。例如:1(很不喜欢)就一定要排在2(有点不喜欢的前面),而2(有点不喜欢)就必须要排在3(一般般的前面)。这个顺序呀,很重要!这就是为什么人们管它叫做“定序数据”。
我们说了,定序数据没有具体的数值意义。因此,我们不能确信:2(有点不喜欢)和1(很不喜欢)的差距,是否正好等于5(超级喜欢)和4(有点喜欢)之间的差距。事实上,基本上不可能相等,因为没那么巧!
既然这些取值之间的间距到底是多少,谁也说不清楚。那么,把很不喜欢定义为Y=1,还是Y=1.5,还是说Y=-3,都无所谓。同样的,如何定义有点不喜欢,也随意。但是只要这个定义,不破坏顺序就可以了。这就是定序数据的核心要义。
定序回归应用的常见的战场有哪些?前面说了,消费者调查,请大家表达自己的偏好。在线下,这就是最普通的市场调研;在线上,就可能是豆瓣上人们对一个电影的打分评级;在医学应用中,有些重要的心理相关的疾病(例如:抑郁症)也会涉及到定序数据。这就是回归分析第三式:定序回归。
简单可加性。
泊松分布能够满足简单可加性。千万不要小看这个性质。该性质让后面的各种统计模型,能够在一个比较一致的框架下被建立起来。而不会是,例如:Y1是泊松分布,Y2是泊松分布,而Y1+Y2需要另外一个分布。这能把建模的人恶心死。泊松分布
在做二分类的问题时,偶们假设数据的分布是满足泊松分布的
什么是计数回归?就是因变量是计数数据的回归分析。那么,什么又是计数数据呢?就是数数的数据。例如,谁家有几个孩子,养了几条狗。
有什么特点?既然是数数,它就必须是**非负的整数**。不能是负数,说谁家有负3个孩子,没这事。不能是小数,例如说谁家养了1.25只狗,也没这说法。
计数数据在哪些地方常见?例如:客户关系管理中,有一个经典的RFM模型,其中这个F,就是frequency,说的是一定时间内,客户到访的次数。可以是0次,也可以是1次、2次、很多次。但是,不能是-2次,更不能是2.3次。这样清楚吗?
计数数据还出现在医学研究中。一个癌症病人体内肿瘤的个数:0是没有,也可以是1个、2个、或者很多个。
计数数据还出现在社会研究中。例如,二胎政策放开,一对夫妻最后到底如何选择要生育多少个孩子呢?可以是0个、1个,也可以是2个。但是,不能是-2个,也不能是0.7个。
要应对计数型因变量,咱就需要回归分析第四式:计数回归。计数回归也有很多招数。最常见的是**泊松回归、负二项回归、零膨胀泊松回归**等方法。欲知详情,请参见各路统计学秘籍。
``
## 生存回归
建https://mp.weixin.qq.com/s?__biz=MzA5MjEyMTYwMg==&mid=2650237580&idx=3&sn=a8753f0f37716db4c24b469814bb4603&chksm=887235e1bf05bcf73606e3e2a021af754cf879810feee5d3385c0f29b714c348505312608d80&scene=21#wechat_redirect
我有点没看太懂标签:大智慧 因变量 无法 回归 看不见 ima 市场 负数 ==
原文地址:https://www.cnblogs.com/gaowenxingxing/p/12956997.html