机器学习实战基础（七）：创建多项式回归器

标签：参数   变量   info   测试   计算   输入数据   详细   虚线   效果   

简介

线性回归模型有一个主要的局限性，那就是它只能把输入数据拟合成直线，而多项式回归模型通过拟合多项式方程来克服这类问题，从而提高模型的准确性。

准备工作

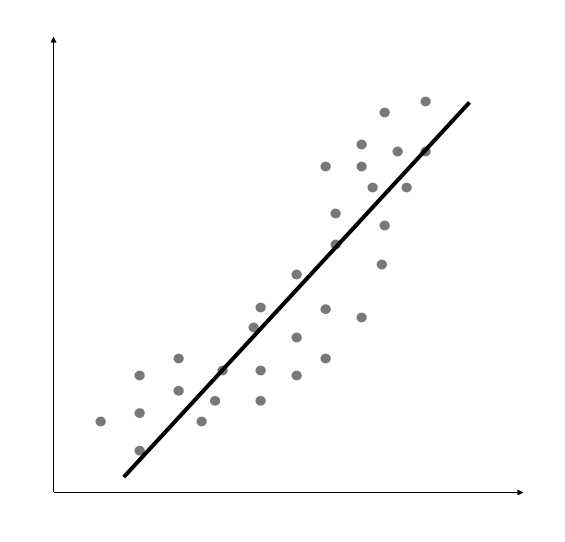
从图1-6中可以看到，数据点本身的模式中带有自然的曲线，而线性模型是不能捕捉到这一点的。再来看看多项式模型的效果，如图1-7所示。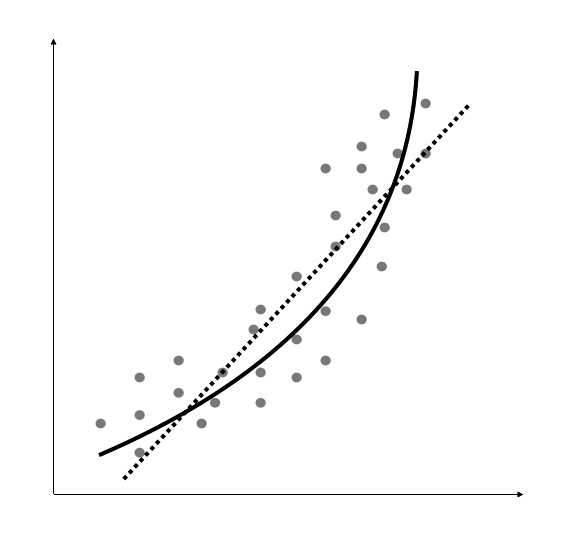

图1-7中的虚线表示线性回归模型，实线表示多项式回归模型。这个模型的曲率是由多项式的次数决定的。
随着模型曲率的增加，模型变得更准确。但是，增加曲率的同时也增加了模型的复杂性，因此拟合速度会变慢。当我们对模型的准确性的理想追求与计算能力限制的残酷现实发
生冲突时，就需要综合考虑了。

详细步骤

(1) 将下面的代码加入Python文件regressor.py中： 

from sklearn.preprocessing import PolynomialFeatures 
 
polynomial = PolynomialFeatures(degree=3) 

(2) 上一行将曲线的多项式的次数的初始值设置为3。下面用数据点来计算多项式的参数：

X_train_transformed = polynomial.fit_transform(X_train) 

其中，X_train_transformed表示多项式形式的输入，与线性回归模型是一样大的。

(3) 接下来用文件中的第一个数据点来检查多项式模型是否能够准确预测： 

datapoint = [0.39,2.78,7.11] 
poly_datapoint = polynomial.fit_transform(datapoint) 
 
poly_linear_model = linear_model.LinearRegression()  
poly_linear_model.fit(X_train_transformed, y_train) 
print "\nLinear regression:", linear_regressor.predict(datapoint) [0] 
print "\nPolynomial regression:", poly_linear_model.predict(poly_datapoint)[0] 

多项式回归模型计算变量数据点的值恰好就是输入数据文件中的第一行数据值。再用线性回归模型测试一下，唯一的差别就是展示数据的形式。运行代码，可以看到下面的结果：

Linear regression: -11.0587294983 
Polynomial regression: -10.9480782122 

可以发现，多项式回归模型的预测值更接近实际的输出值。如果想要数据更接近实际输出值，就需要增加多项式的次数。
(4) 将多项式的次数加到10看看结果： 

polynomial = PolynomialFeatures(degree=10) 

可以看到下面的结果：
Polynomial regression: -8.20472183853
现在，你可以发现预测值与实际的输出值非常地接近。

机器学习实战基础（七）：创建多项式回归器

标签：参数   变量   info   测试   计算   输入数据   详细   虚线   效果   

原文地址：https://www.cnblogs.com/qiu-hua/p/12979834.html