标签:hold 图片 import sklearn sel play 经验 style 情况
方差挑选完毕之后,我们就要考虑下一个问题:相关性了。
我们希望选出与标签相关且有意义的特征,因为这样的特征能够为我们提供大量信息。如果特征与标签无关,那只会白白浪费我们的计算内存,可能还会给模型带来噪
音。在sklearn当中,我们有三种常用的方法来评判特征与标签之间的相关性:卡方,F检验,互信息。
卡方过滤是专门针对离散型标签(即分类问题)的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量,并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest这个可以输入”评分标准“来选出前K个分数最高的特征的类,我们可以借此除去最可能独立于标签,与我们分类目的无关的特征。
另外,如果卡方检验检测到某个特征中所有的值都相同,会提示我们使用方差先进行方差过滤。并且,刚才我们已经验证过,当我们使用方差过滤筛选掉一半的特征后,模型的表现时提升的。因此在这里,我们使用threshold=中位数时完成的方差过滤的数据来做卡方检验(如果方差过滤后模型的表现反而降低了,那我们就不会使用方差过滤后的数据,而是使用原数据):
from sklearn.ensemble import RandomForestClassifier as RFC from sklearn.model_selection import cross_val_score from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 #假设在这里我一直我需要300个特征 X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y) X_fschi.shape
#验证一下模型的效果如何
cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()
可以看出,模型的效果降低了,这说明我们在设定k=300的时候删除了与模型相关且有效的特征,我们的K值设置得太小,要么我们需要调整K值,要么我们必须放弃相关性过滤
。当然,如果模型的表现提升,则说明我们的相关性过滤是有效的,是过滤掉了模型的噪音的,这时候我们就保留相关性过滤的结果。
那如何设置一个最佳的K值呢?在现实数据中,数据量很大,模型很复杂的时候,我们也许不能先去跑一遍模型看
看效果,而是希望最开始就能够选择一个最优的超参数k。那第一个方法,就是我们之前提过的学习曲线:
#======【TIME WARNING: 5 mins】======# %matplotlib inline import matplotlib.pyplot as plt score = [] for i in range(390,200,-10): X_fschi = SelectKBest(chi2, k=i).fit_transform(X_fsvar, y) once = cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean() score.append(once) plt.plot(range(350,200,-10),score) plt.show()
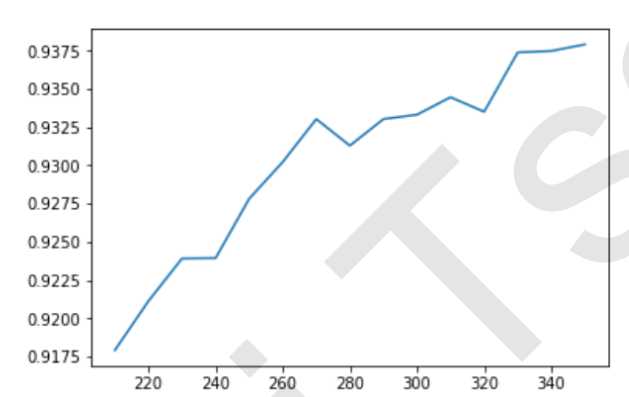
通过这条曲线,我们可以观察到,随着K值的不断增加,模型的表现不断上升,这说明,K越大越好,数据中所有的特征都是与标签相关的。但是运行这条曲线的时间同样也是非常地长,接下来我们就来介绍一种更好的选择k的方法:看p值选择k。
卡方检验的本质是推测两组数据之间的差异,其检验的原假设是”两组数据是相互独立的”。卡方检验返回卡方值和P值两个统计量,其中卡方值很难界定有效的范围,而p值,我们一般使用0.01或0.05作为显著性水平,即p值判断的边界,具体我们可以这样来看: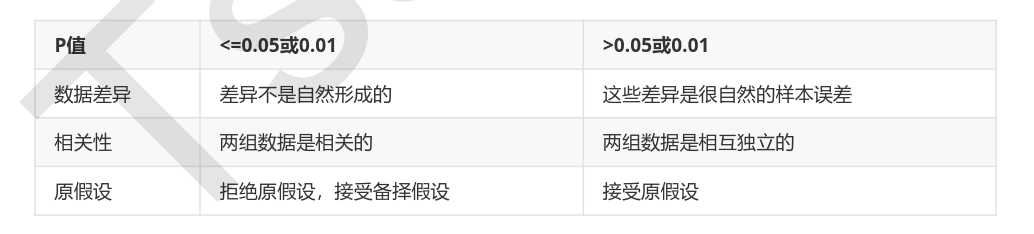
从特征工程的角度,我们希望选取卡方值很大,p值小于0.05的特征,即和标签是相关联的特征。而调用SelectKBest之前,我们可以直接从chi2实例化后的模型中获得各个特征所对应的卡方值和P值。
chivalue, pvalues_chi = chi2(X_fsvar,y) chivalue pvalues_chi #k取多少?我们想要消除所有p值大于设定值,比如0.05或0.01的特征: k = chivalue.shape[0] - (pvalues_chi > 0.05).sum() #X_fschi = SelectKBest(chi2, k=填写具体的k).fit_transform(X_fsvar, y) #cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()
可以观察到,所有特征的p值都是0,这说明对于digit recognizor这个数据集来说,方差验证已经把所有和标签无关的特征都剔除了,或者这个数据集本身就不含与标签无关的特征。
在这种情况下,舍弃任何一个特征,都会舍弃对模型有用的信息,而使模型表现下降,因此在我们对计算速度感到满意时,我们不需要使用相关性过滤来过滤我们的数据。如果我们认为运算速度太缓慢,那我们可以酌情删除一些特征,但前提是,我们必须牺牲模型的表现。接下来,我们试试看用其他的相关性过滤方法验证一下我们在这个数据集上的结论。
F检验,又称ANOVA,方差齐性检验,是用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类,因此包含feature_selection.f_classif(F检验分类)和feature_selection.f_regression(F检验回归)两个类。其中F检验分类用于标签是离散型变量的数据,而F检验回归用于标签是连续型变量的数据。
和卡方检验一样,这两个类需要和类SelectKBest连用,并且我们也可以直接通过输出的统计量来判断我们到底要设置一个什么样的K。需要注意的是,F检验在数据服从正态分布时效果会非常稳定,因此如果使用F检验过滤,我们会先将数据转换成服从正态分布的方式。
F检验的本质是寻找两组数据之间的线性关系,其原假设是”数据不存在显著的线性关系“。它返回F值和p值两个统计量。和卡方过滤一样,我们希望选取p值小于0.05或0.01的特征,这些特征与标签时显著线性相关的,而p值大于0.05或0.01的特征则被我们认为是和标签没有显著线性关系的特征,应该被删除。以F检验的分类为例,我们继续在数字数据集上来进行特征选择:
from sklearn.feature_selection import f_classif F, pvalues_f = f_classif(X_fsvar,y) F pvalues_f k = F.shape[0] - (pvalues_f > 0.05).sum() #X_fsF = SelectKBest(f_classif, k=填写具体的k).fit_transform(X_fsvar, y) #cross_val_score(RFC(n_estimators=10,random_state=0),X_fsF,y,cv=5).mean()
得到的结论和我们用卡方过滤得到的结论一模一样:没有任何特征的p值大于0.01,所有的特征都是和标签相关的,因此我们不需要相关性过滤。
互信息法是用来捕捉每个特征与标签之间的任意关系(包括线性和非线性关系)的过滤方法。和F检验相似,它既可以做回归也可以做分类,并且包含两个类feature_selection.mutual_info_classif(互信息分类)和feature_selection.mutual_info_regression(互信息回归)。这两个类的用法和参数都和F检验一模一样,不过
互信息法比F检验更加强大,F检验只能够找出线性关系,而互信息法可以找出任意关系。
互信息法不返回p值或F值类似的统计量,它返回“每个特征与目标之间的互信息量的估计”,这个估计量在[0,1]之间取值,为0则表示两个变量独立,为1则表示两个变量完全相关。以互信息分类为例的代码如下:
from sklearn.feature_selection import mutual_info_classif as MIC result = MIC(X_fsvar,y) k = result.shape[0] - sum(result <= 0) #X_fsmic = SelectKBest(MIC, k=填写具体的k).fit_transform(X_fsvar, y) #cross_val_score(RFC(n_estimators=10,random_state=0),X_fsmic,y,cv=5).mean()
所有特征的互信息量估计都大于0,因此所有特征都与标签相关。
当然了,无论是F检验还是互信息法,大家也都可以使用学习曲线,只是使用统计量的方法会更加高效。当统计量判断已经没有特征可以删除时,无论用学习曲线如何跑,删除特征都只会降低模型的表现。当然了,如果数据量太庞大,模型太复杂,我们还是可以牺牲模型表现来提升模型速度,一切都看大家的具体需求。
机器学习实战基础(十五):sklearn中的数据预处理和特征工程(八)特征选择 之 Filter过滤法(二) 相关性过滤
标签:hold 图片 import sklearn sel play 经验 style 情况
原文地址:https://www.cnblogs.com/qiu-hua/p/12986763.html