标签:size turn 一段 另一个 证明 方便 二分 inline 调用
k,请统计这棵树上总长度小于等于k的路径个数。路径长度为路径路径上所有边的权值和。POJ 1741。dfs一遍求出任一点到根的距离,枚举每一条路径u~v,通过LCA(u,v),求出路径的长度。时间效率为:\(O(n^2log(n))\) 。假设一条满足条件的路径经过点 x ,那么这条路径在 x 的一个子树里(以 x 为端点)或者在 x 的两个不同的子树里,如图:

假设我们选出一个根 Root ,那么答案路径存在两种情况:
Root ,在黑子树中选择一部分路径,在红子树中选择一部分路径,然后从 Root 处拼起来形成一条答案路径.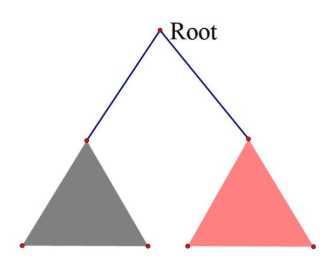
仔细想一下,发现情况1(被一个子树包含)中,答案路径上的一点变为根 Root ,就成了情况2(在两棵子树中)。
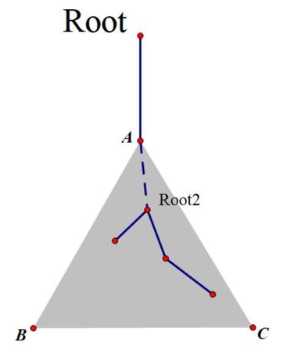
如图, Root 为根的子树中存在答案(蓝色实边路径),可以看成以 Root2 为根的两棵子树存在答案,所以只用处理情况2就行了,可以用分治的方法,这应该是点分治的基本原理。
首先根不能随便选,选根不同会影下面遍历的效率的,如图:
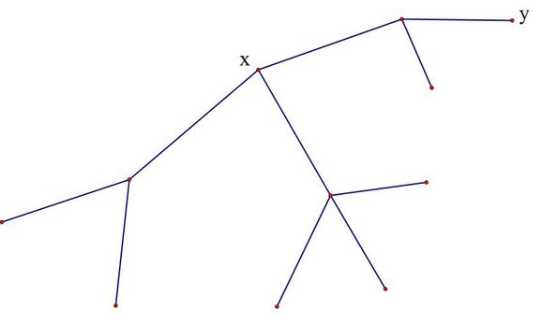
x为根比选y为根更优,选 x 最多递归2层,选 y 最多递归4层,显然可以发现找树的重心(重心所有的子树的大小都不超过整个树大小的一半)是最优的。1递归处理。按照上述步骤实现代码:
DFS来实现。DFS计算。DFS函数,再递归求解即可。计算重心
void GetRoot(int u,int f){
siz[u]=1;wt[u]=0;//siz[u]:u为根的子树节点数;wt[u]:u的节点最大的子树节点数
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v!=f && !vis[v]){//vis[v]==1说明v是当前子树的父亲节点,如下图
GetRoot(v,u);//递归求子树v的重心
siz[u]+=siz[v];//累计u的子树大小
wt[u]=std::max(wt[u],siz[v]);//求u的最大子树
}
}//Tsiz[u]-siz[u]表示u的父亲节点除u以外其它子树之和,如下图,如果u=2,则把1子树也当做2的一个子树
wt[u]=std::max(wt[u],Tsiz-siz[u]);//利用的是无根树的特点
if(wt[Root]>wt[u])Root=u;//w[root]初始化为Inf,相当于求最大子树最小的节点u,即为重心
}
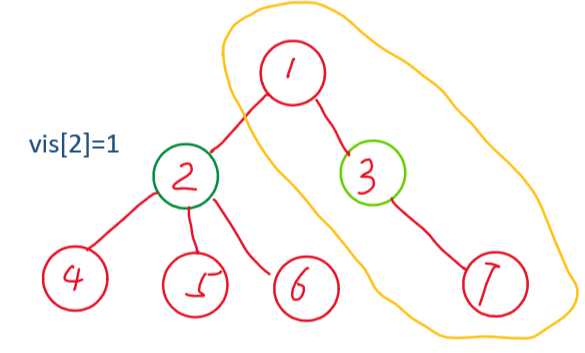
2为整个子树的重心,节点3为节点2以1为根的子树的重心。我们以重心3来求点分治的时候不能访问到2及2的其他子树。计算满足条件的答案
void dfs(int u,int f,int d){//求以u为根的子树中其他点到u的距离+初始值d
a[++cnt]=d;//u到距离为d的祖先节点也是一条路径
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v!=f && !vis[v])//vis同上图,截断子树的范围
dfs(v,u,d+e[i].w);
}
}
int Calc(int u,int d){
cnt=0;//记录u为根的子树中经过u路径条数
dfs(u,0,d);//把经过u的路径的长度存储到a[1]~a[cnt]
std::sort(a+1,a+cnt+1);//从小到大排序
int sum=0;//计算满足条件的路径条数
for(int i=1,j=cnt;;++i){//双指针技巧求满足条件的组合数,比二分快
while(j && a[i]+a[j]>k)--j;//找到当前和a[i]组合的最大的a[j]
if(i>j)break;//说明找不到一个满足和a[i]组合的另一条链
sum+=j-i+1;//a[i]~a[j]的链都能和a[i]组合,包括a[i]单链
}//计算的组合包含共用同一段链的情况,如下图
return sum;
}
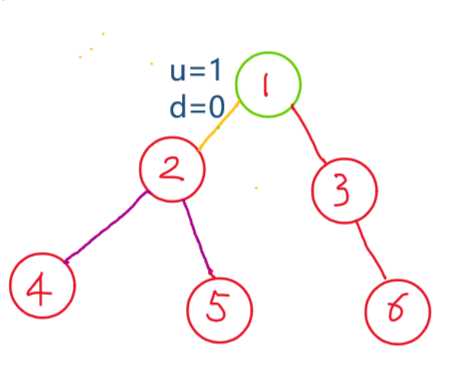
1为根计算路径的时候a[4]记录的1-2-4路径长度,a[5]记录的1-2-4路径的长度,他们共用了1-2这条边,点分治的核心思想,即路径要经过根节点,4~5的路径并不经过此时的根几点1,这需要我们在后面的计算中去掉。点分治核心代码
void DFS(int u){
ans+=Calc(u,0);//计算u为根的子树满足条件两条路径之和小于等于k的条数(包括共边路径组合)
vis[u]=1;//标记以u为重心的子树已计算
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(!vis[v]){//避免越界
ans-=Calc(v,e[i].w);//减去共边为u-v且满足条件的条数
Root=0;Tsiz=siz[v];//求以v为根子树的重心,Root记录子树的重心
GetRoot(v,0);
DFS(Root);//子树v从重心求解满足条件的组合,是一个递归的子问题
}
}
}
完整代码POJ 1741
#include <cstdio>
#include <cstring>
#include <algorithm>
const int maxn = 1e4 + 5,Inf=0x3f3f3f3f;
struct Edge{int to,w,next;}e[2*maxn];
int n,k,ans,Root,Tsiz,cnt;
int head[maxn],siz[maxn],wt[maxn],a[maxn];
bool vis[maxn];
void Insert(int u,int v,int w){
e[++head[0]].to=v;e[head[0]].w=w;e[head[0]].next=head[u];head[u]=head[0];
}
void GetRoot(int u,int f){
siz[u]=1;wt[u]=0;//siz[u]:u为根的子树节点数;wt[u]:u的节点最大的子树节点数
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v!=f && !vis[v]){//vis[v]==1说明v是当前子树的父亲节点,如下图
GetRoot(v,u);//递归求子树v的重心
siz[u]+=siz[v];//累计u的子树大小
wt[u]=std::max(wt[u],siz[v]);//求u的最大子树
}
}//Tsiz[u]-siz[u]表示u的父亲节点除u以外其它子树之和,如下图,如果u=2,则把1子树也当做2的一个子树
wt[u]=std::max(wt[u],Tsiz-siz[u]);//利用的是无根树的特点
if(wt[Root]>wt[u])Root=u;//w[root]初始化为Inf,相当于求最大子树最小的节点u,即为重心
}
void dfs(int u,int f,int d){//求以u为根的子树中其他点到u的距离+初始值d
a[++cnt]=d;//u到距离为d的祖先节点也是一条路径
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v!=f && !vis[v])//vis同上图,截断子树的范围
dfs(v,u,d+e[i].w);
}
}
int Calc(int u,int d){
cnt=0;//记录u为根的子树中经过u路径条数
dfs(u,0,d);//把经过u的路径的长度存储到a[1]~a[cnt]
std::sort(a+1,a+cnt+1);//从小到大排序
int sum=0;//计算满足条件的路径条数
for(int i=1,j=cnt;;++i){//双指针技巧求满足条件的组合数,比二分快
while(j && a[i]+a[j]>k)--j;//找到当前和a[i]组合的最大的a[j]
if(i>j)break;//说明找不到一个满足和a[i]组合的另一条链
sum+=j-i+1;//a[i]~a[j]的链都能和a[i]组合,包括a[i]单链
}//计算的组合包含共用同一段链的情况,如下图
return sum;
}
void DFS(int u){
ans+=Calc(u,0);//计算u为根的子树满足条件两条路径之和小于等于k的条数(包括共边路径组合)
vis[u]=1;//标记以u为重心的子树已计算
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(!vis[v]){//避免越界
ans-=Calc(v,e[i].w);//减去共边为u-v且满足条件的条数
Root=0;Tsiz=siz[v];//求以v为根子树的重心,Root记录子树的重心
GetRoot(v,0);
DFS(Root);//子树v从重心求解满足条件的组合,是一个递归的子问题
}
}
}
void Solve(){
while(~scanf("%d%d",&n,&k) && n && k){
ans=0;memset(vis,0,sizeof(vis));
memset(head,0,sizeof(head));
for(int i=1;i<n;++i){
int u,v,w;scanf("%d%d%d",&u,&v,&w);
Insert(u,v,w);Insert(v,u,w);
}
wt[0]=Inf;//初始化重心所在子树节点数位无穷大,方便求重心,所以每次求子树重心前必须把root=0
Root=0;Tsiz=n;GetRoot(1,0);//可以随便从一个节点开始求重心,这里我们从节点1开始
DFS(Root);//从重心Root开始求满足条件的组合
printf("%d\n",ans-n);//每个单点我们计算是都当做了一条路径,需要减去
}
}
int main(){
Solve();
return 0;
}
标签:size turn 一段 另一个 证明 方便 二分 inline 调用
原文地址:https://www.cnblogs.com/hbhszxyb/p/12988533.html