第五章感想

标签：space   ==   先序   顺序存储   image   include   cin   alt   else   

第五章学习了树与二叉树等相关内容

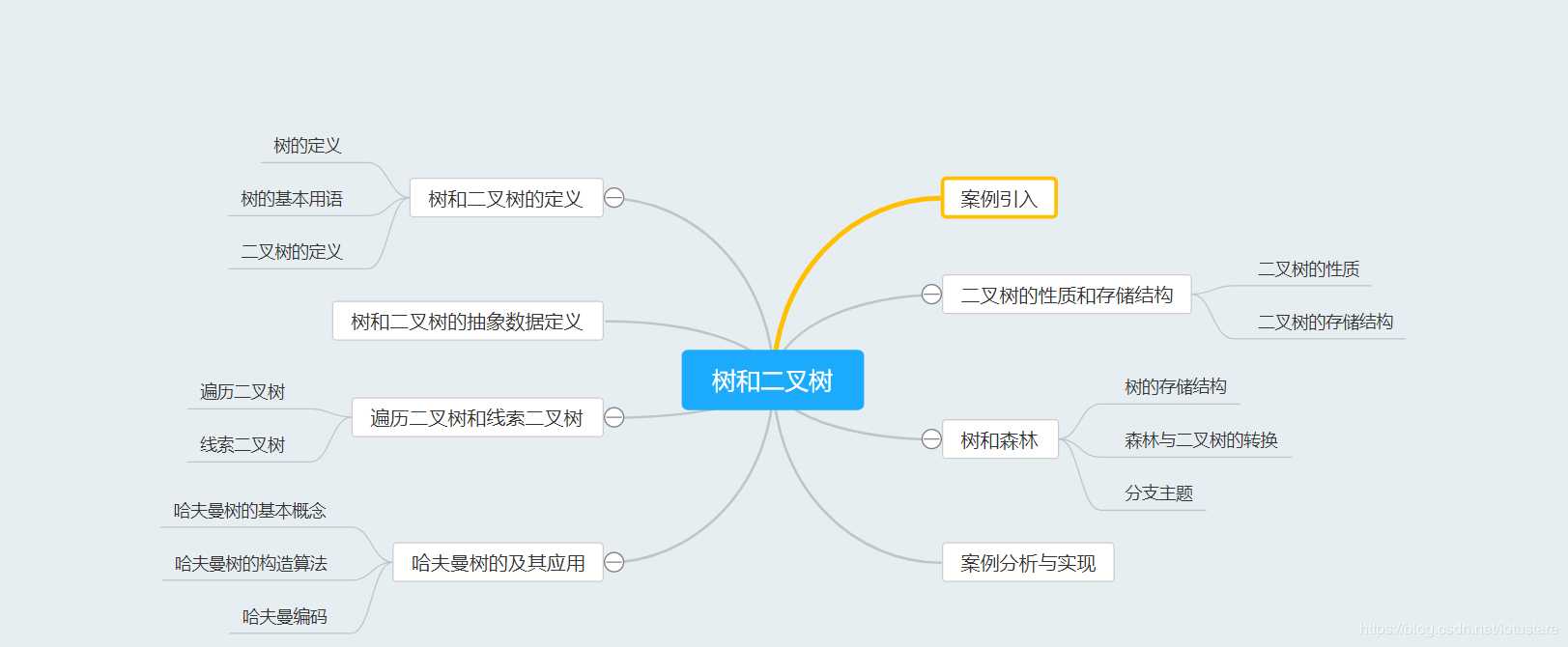
 具体有如何去遍历一颗二叉树，分为层次遍历，先序遍历，中序遍历和后序遍历。其次还有最优的哈夫曼树，怎么去构造一棵哈夫曼树，从低往上构造等等。以及树的构造中会用到的链式存储及顺序存储结构还有借助数组来解决相关问题，定义树时采用的是递归的方式。

#include<iostream>

using namespace std;

typedef struct node{

int lchild;
int rchild;
bool root=true;
}node;//定义结点

int main(){
int n;
cin>>n;
node bt[n];
char l,r;
int root1;
int tree[n];
int isfirst=1;
for(int i=0;i<n;i++){
cin>>l>>r;
if(l==‘-‘){
bt[i].lchild=-1;//将‘-’赋值为-1，以便找到叶子结点
}
else{
bt[i].lchild=l-‘0‘;
bt[l-‘0‘].root=false; //将出现的结点标记root为false，以找到根结点。
}
if(r==‘-‘){
bt[i].rchild=-1;
}
else{
bt[i].rchild=r-‘0‘;
bt[r-‘0‘].root=false;//右孩子也一样的操作
}
}
//找到根节点
for(int i=0;i<n;i++){
if(bt[i].root==true){
root1=i;
}
}

//层序遍历保存结点的值
int j=0;
tree[j++]=root1;
for(int i=0;i<n;i++){
if(bt[tree[i]].lchild!=-1){
tree[j++]=bt[tree[i]].lchild;
}
if(bt[tree[i]].rchild!=-1){
tree[j++]=bt[tree[i]].rchild;
}
}

for(int i=0;i<n;i++){
if(bt[tree[i]].lchild==-1&&bt[tree[i]].rchild==-1){
if(isfirst){
cout<<tree[i];
isfirst=0;//叶子结点的条件
}
else{
cout<<" "<<tree[i];
}
}
}
return 0;
}

第五章感想

标签：space   ==   先序   顺序存储   image   include   cin   alt   else   

原文地址：https://www.cnblogs.com/1905crr/p/12992745.html