标签:树的定义 mda 深度 导图 void com code 相同 字符编码
大纲式思维导图
树
基本术语:结点的度(结点的子树个数)、树的度、叶结点(度为0)、父结点、兄弟结点、路径和路径长度、祖先结点、子孙结点、结点的层次、树的深度(注意根结点深度为1,而不是0)
二叉树的定义(五种基本形态)
完美二叉树(满二叉树)、完全二叉树(编号为 i 的结点与满二叉树中编号为 i 的结点在二叉树中位置相同)
性质1:1个二叉树第 i 层的最大结点树为2的(i-1)次方
性质2:深度为 k 的二叉树有最大结点总数为(2的 k 次方 - 1)
性质3:对任何非空二叉树T,若n0表示叶结点的个数,n2是度为2的非叶结点个数,那么两者满足关系n0 = n2 + 1(经常碰到考性质3的题目)
性质4:具有 n 个结点的完全二叉树的深度为 (不大于 以2为底的 n 的对数 的最大整数 + 1)
贴一道作业题:
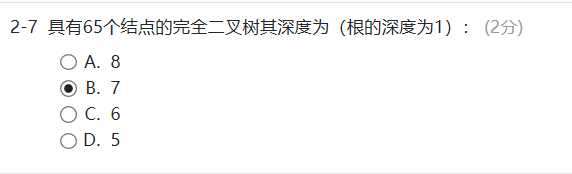
性质5:如果对一棵有 n 个结点的完全二叉树(深度由性质4求得)的结点按层序(从上到下、从左到右)编号,则对任一结点 i 有,
(1)如果 i = 1,则结点 i 是二叉树的根,无双亲;如果 i > 1, 则其双亲结点Parent( i )是不大于 (i / 2) 的最大整数;
(2)如果 2 * i > n, 则结点 i 无左孩子;否则其左孩子是结点 2 * i ;
(3)如果 2 * i + 1 > n, 则结点 i 无右孩子;否则其右孩子是结点(2 * i + 1);
二叉树的抽象数据类型定义(翻笔记)
二叉树的存储结构
顺序存储结构


链表存储结构

遍历二叉树(层序、先序、中序、后序,在这里举先序遍历的代码)
void PreOrderTraversal ( BiTree T ) { if ( T != NULL ) { cout << T->data ; //访问根结点 PreOrderTraverse ( T->lchild ) ; //递归 PreOrderTraverse ( T->rchild ) ; } }
树的存储结构
双亲表示法 结点结构:
| data | parent |
双亲孩子表示法
结点结构:
| data | parent | firstchild |
孩子兄弟表示法
typedef struct Node { int data ; struct Node *firstchild, *nextsibling ; } Node ; typedef struct Tree { Node a [ MAX ] ; int root ; }Tree, *TreeNode ;
森林与二叉树的转换——左孩子,右兄弟
森林的遍历——相当于多棵树的遍历,按照顺序逐棵逐棵进行
哈夫曼树
基本概念:路径、路径长度、带权路径长度、哈夫曼树(最优二叉树)、WPL = 每个字符编码的长度 * 每个字符出现的次数 之和 (出现次数多的结点应该尽量靠近根结点,使编码长度变短)【第5章讨论题:论证哈夫曼树的WPL小于等于任一二叉树】
哈夫曼树的构造:自底向上(从叶子结点开始构造,最后构造的是根结点),越早被构造出来的叶子结点,离根结点越远,它的哈夫曼编码也就越长
哈夫曼树的构造算法:
顺序存储结构
类型定义
typedef struct {
int weight ; //权
int parent, lch, rch ; //父结点编号、左孩子编号、右孩子编号
} *Huffman Tree ;
算法思路:(1)初始化:HT [ 1......(2 * n - 1)] : lch = rch = parent = 0 ;
(2)输入初始 n 个结点:置HT [ 1......(2 * n - 1)] 的 weight 值 ;
(3)for ( i = n + 1 ; i <= 2 *n - 1 ; i++ ) {
//进行 n-1 次合并,依次产生HT[ i ]
//选两个未被选过的weight最小的结点
s1, s2 = min { k < i && HT [ k ].parent = 0 } ;
HT [ s1 ].parent = HT [ s2 ].parent = i ;
HT [ i ].weight = HT [ s1 ].weight + HT [ s2 ].weight ;
HT [ i ].lch = s1 ; HT [ i ].rch = s2 ;
}
手工实现哈夫曼树(画表、画树、计算WPL)翻笔记
代码部分
1、做树的题时常常需要用到递归思路,但迭代(创建队列)也可以完成,但迭代的代码还无法理解;
2、第五章作业题(求二叉树的叶子结点个数)
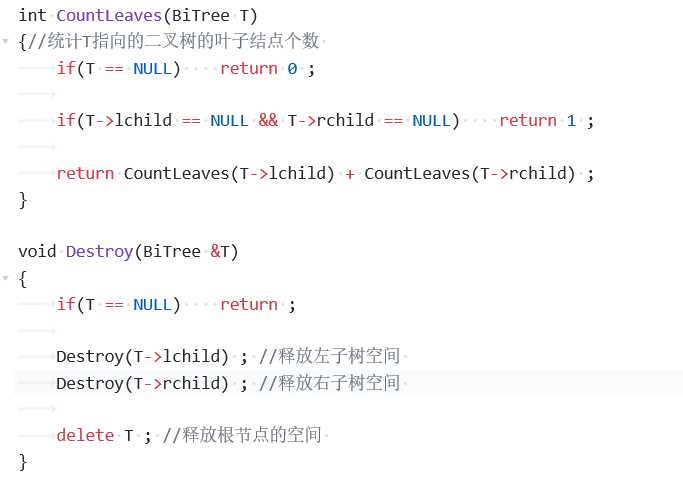
这道题里学到最多的是这两个函数,在 CountLeaves 函数里,它是利用了叶子结点度为0的特点,让我明白了如何根据定义去找做题思路,而且对叶子结点度为0这一特点有了深刻的认识;在 Destroy 函数里,觉得递归的做法很巧妙,代码很好理解,让人眼前一亮。
3、第五章实践一 第1题(List Leaves)
typedef struct {//如果读取的是‘-’,那就把值定为-1 int lch ; //左孩子 int rch ; //右孩子 }Node ; typedef struct { Node data[10] ; int root ; //根结点的编号 }Tree ; void Create(Tree &T) {//读入数据,同时找出根结点 int n ; cin >> n ; bool check[10] = {false} ; char a, b ; for(int i=0 ; i<n ; i++) { cin >> a >> b ; if(a == ‘-‘) T.data[i].lch = -1 ; else { T.data[i].lch = a - ‘0‘ ; check[a - ‘0‘] = true ; } if(b == ‘-‘) T.data[i].rch = -1 ; else { T.data[i].rch = b - ‘0‘ ; check[b - ‘0‘] = true ; } } //找出根结点,写入到T.root for(int i=0 ; i<n ; i++) { if(check[i] == false) { T.root = i ; break ; } } } void LevelOrder(Tree T) { queue<int> Q ; //定义队列 Q.push(T.root) ; //根结点首先入队 int k ; bool flag = false ; while(!Q.empty()) { k = Q.front() ; //获取队头元素 Q.pop() ; //队头元素出队 //判断k是否为叶子结点,如果是则直接输出 if(T.data[k].lch == -1 && T.data[k].rch == -1) { if(flag == false) { cout << k ; flag = true ; } else cout << " " << k ; } else {//如果不是叶子结点,那么将它的孩子结点入队 if(T.data[k].lch != -1) Q.push(T.data[k].lch) ; if(T.data[k].rch != -1) Q.push(T.data[k].rch) ; } } }
这道题里干货满满,很多其他题目的类型定义基本也是这个套路,Create 函数里的 check 函数用得很巧妙,让找根结点的操作变得很清晰,便于理解,T.data [ i ].lch 在敲代码时要小心别写错了;在LevelOrder函数里,运用队列 “先进先出” 的特性来做题,也是感觉四两拨千斤,而且以后在做题时难以理清树的结点的存放顺序时,可以多多借用队列这种结构,看到很多题目都是这么处理的。
标签:树的定义 mda 深度 导图 void com code 相同 字符编码
原文地址:https://www.cnblogs.com/cq20/p/13021516.html