标签:targe blank 继承 最大值 树结构 mil 线段 回溯 htm
前言
不知道为啥原网站竟然没有对树——数据结构最为重要的基本结构(没有之一)——有单独的介绍板块,我觉得必不可少!后面众多高级数据结构都是以树为结构的,所以这一部分很必要。
子目录列表
1、
2、
7.3 树与二叉树
1、形象的树
如果你说你不知道栈是什么,队列是什么,链是什么,树就不可能不知道了 —— 各式各样的树遍布大街小巷,它或如柳树般翩翩淑女,或如槐树般魁梧高大,但它们的结构却有鲜明的共同特点:扎根于地,向上生长,生出分枝,分枝再生出更小的分枝。
而作为数据结构的一种,树和客观世界中的树极其相似:
① 不同于栈,队列,数组等线性表,树是一种非线性结构,是由 n(n >= 0) 个结点组成的有限集;
② n >= 1 时,结点中有且仅有一个结点被称为根结点;
③ n >= 2 时,除去根结点,其余 n - 1 个结点是 m 个互不相交的结点有限集,又可以看做 m 棵树,并且都被称作根的子树;
④ 对于这 m 棵子树,它们都有自己的根结点,即与整棵树的根结点直接相连的那个结点。对于任意一棵子树,除去其根结点,其余结点又是若干个互不相交的结点有限集,依次递归;
⑤ 如果结点除去与其直接相连的所属子树的根结点而没有其他相连结点,则这个结点称为叶子结点。
上述就是对抽象数据类型树的定义。
正如其名,确实很抽象,拿出一棵树来展示一下:
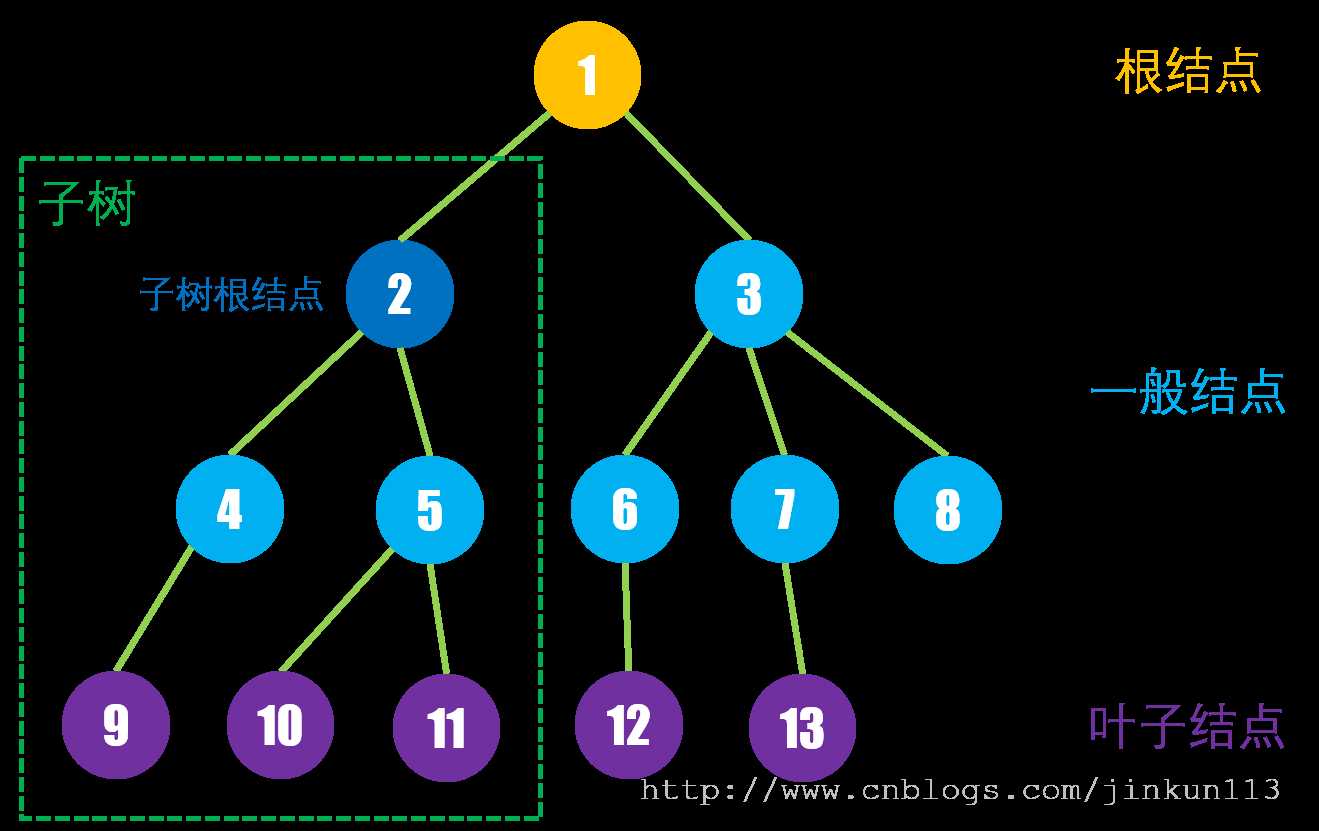
从上述过程不难看出,树的构建和遍历过程是需要通过递归(请参见:2.2 递归与分治)完成的 —— 从根结点递归到叶子结点,再回溯。
而结合家族族谱来看树结构,对其许多相关术语就能轻松理解,还是上图:
假设这是张三家的族谱,张三的编号为 9,那么根结点 1 是他的曾祖父,2 是他的祖父,4 是他的父亲,对于其他结点,也是这样的关系,所以:
① 对于 4 而言,9 是它的儿子结点,反之,4 是 9 的父亲结点;
② 对于 10 而言,11 是它的兄弟结点,4 和 5 同理;
③ 对于 9 而言,10, 11 是它的堂兄弟结点,12 和 13 同理;
④ 对于 1 而言,2 ~ 13 所有结点都是它的子孙结点,反之,1 是 2 ~ 13 的祖先结点。
除此之外,还有:
① 度:结点拥有的子树个数称为结点的度;各结点的度的最大值称为树的度;
比如,9 的度为 0,5 的度为 2,3 的度为 3,这棵树的度为 3。
② 层次:根结点的层次定义为第一层,其儿子结点为第二层,以此类推。也就是说,同层次的所有非兄弟结点可互称为堂兄弟;
③ 深度:所有结点层次的最大值为树的深度;
比如,这棵树的深度为 4。
还有一些概念:
① 有序树和无序树:有序树中的子结点存在次序,比如对于 1 而言,2 是它的第一个儿子节点,3 是第二个;无序树则不存在。
② 森林:m 棵互不相交的树的集合。对于非叶子结点而言,其子树的集合即是一片森林。
2、二叉树
① 概念
二叉树是一种特殊的树形结构,它的每个结点至多只有 2 棵子树,即不存在度 > 2 的结点。放在家族族谱里,可以理解为这个家族所在的国家实行 Family Planning 政策,至多只能生 2 个儿子。
二叉树属于有序树,即对于任意一个非叶子结点,其子树有左右之分,其儿子结点分为左儿子结点和右儿子结点,如下图。
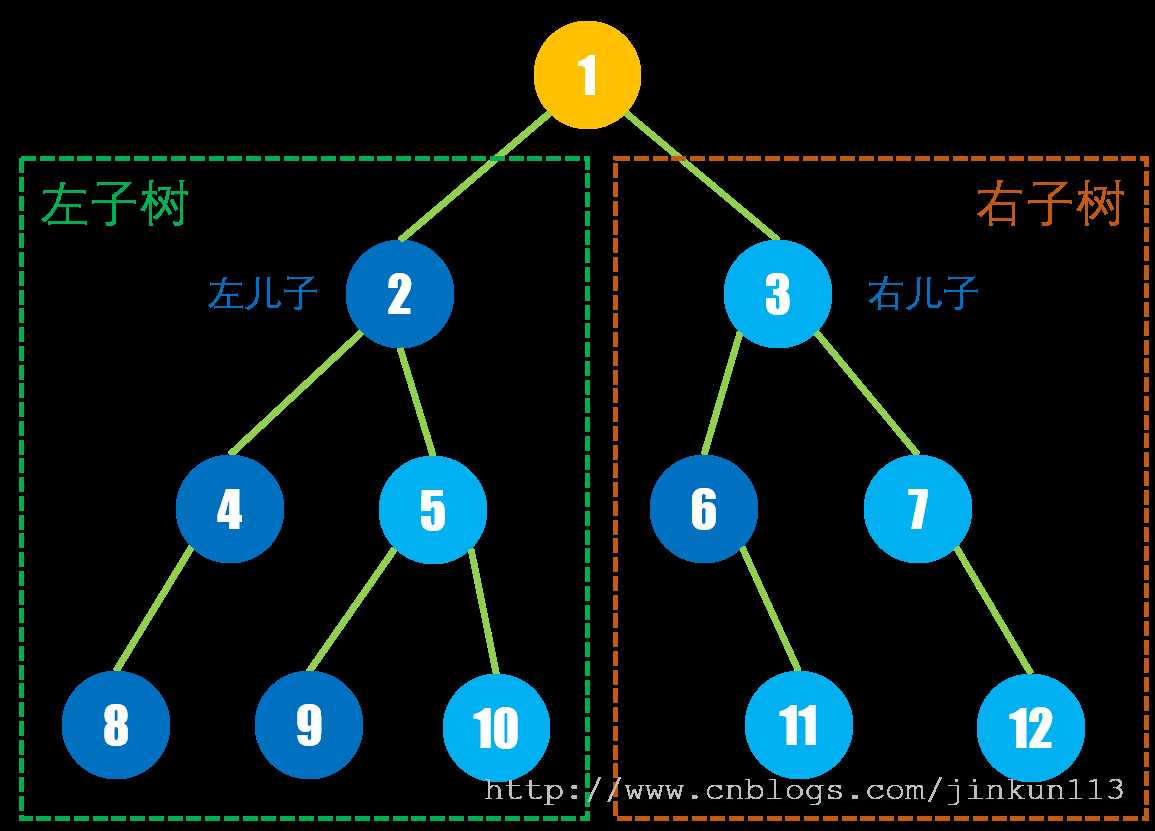
二叉树继承所有树结构的性质和术语,此外还有其独有的性质。
> 第 i 层至多有 2 ^ (i - 1) 个结点;
> 深度为 k 的二叉树至多有 2 ^ k - 1 个结点;
② 特殊二叉树
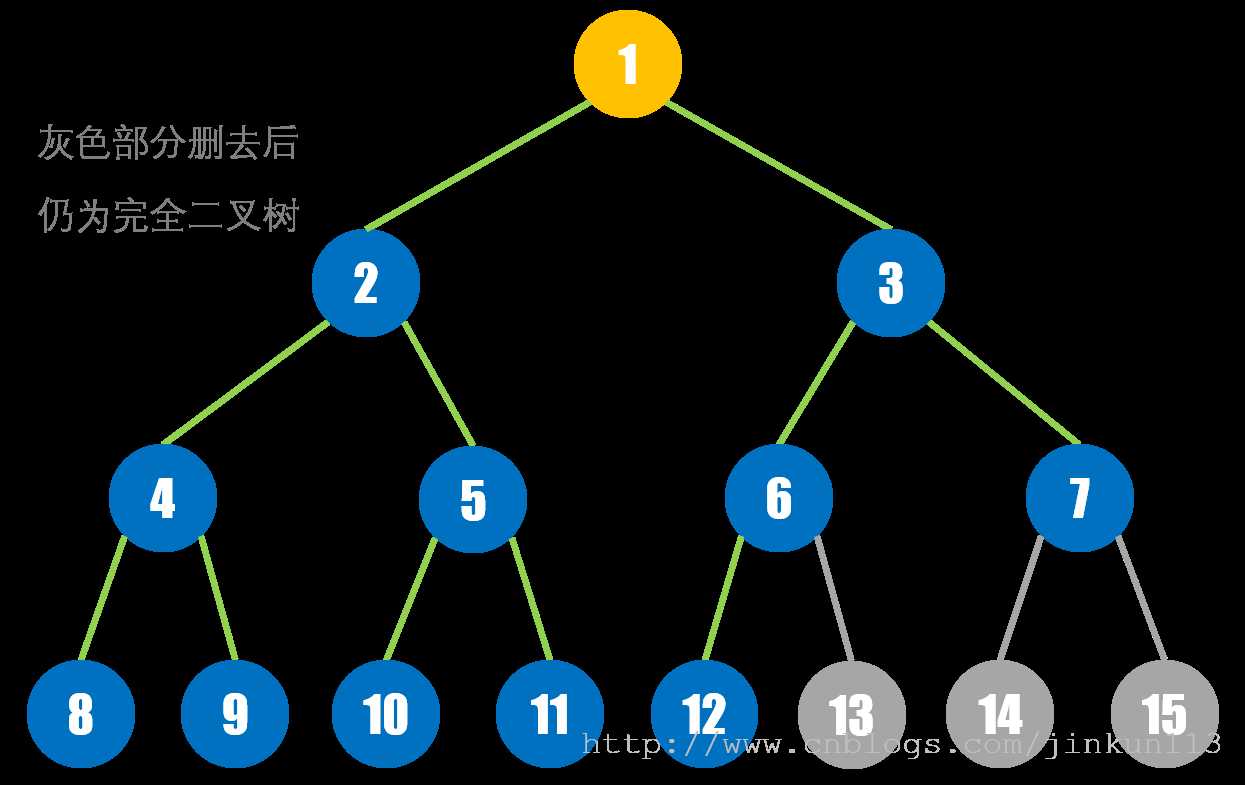
> 一棵深度为 k 且有 2 ^ k - 1 个结点的二叉树称为满二叉树。即除了叶子结点,所有结点都有 2 个儿子节点。
> 在满二叉树的基础上,允许叶子结点的父亲结点所属的层次没有叶子结点,这样的二叉树称为完全二叉树。满二叉树是完全二叉树的一种。
见下图。
③ 二叉树的存储
> 顺序存储结构
因为结构单一,完全二叉树可以考虑用顺序存储结构,即在数组中就能完成对二叉树的数据存储。假设读入二叉树数组 a[i],其第 i 位表示第 i 个结点,而由上图就可以看出,第 i 个结点的左儿子结点为 i * 2,右儿子结点为 i * 2 + 1。
线段树就属于完全二叉树的一种,一般采用顺序存储结构。
而非完全二叉树的结点编号没这么简单,这时候就需要链式存储结构。
> 链式存储结构
链表相比数组更擅长处理结点之间的关系,链式存储结构相比顺序存储结构也是如此。每一个结点数据由权值,左儿子指针和右儿子指针组成。有必要的话,还可以增加父亲指针,以便于向上寻找祖先。它适用于所有二叉树。
4、遍历二叉树
5、
标签:targe blank 继承 最大值 树结构 mil 线段 回溯 htm
原文地址:https://www.cnblogs.com/jinkun113/p/13022494.html