标签:art 解决 大于 ace shm source while 中间 china
堆(Heap)是一个可以被看成近似完全二叉树的数组。树上的每一个结点对应数组的一个元素。除了最底层外,该树是完全充满的,而且是从左到右填充。—— 来自:《算法导论》
堆包括最大堆和最小堆:最大堆的每一个节点(除了根结点)的值不大于其父节点;最小堆的每一个节点(除了根结点)的值不小于其父节点。
堆常见的操作:
堆结构的一个常见应用是建立优先队列(Priority Queue)。
问题列表:
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。例如,[2,3,4]?的中位数是 3;[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例:
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
进阶:
- 如果数据流中所有整数都在 0 到 100 范围内,你将如何优化你的算法?
- 如果数据流中 99% 的整数都在 0 到 100 范围内,你将如何优化你的算法?
分析:图片转自这里(感谢作者~)
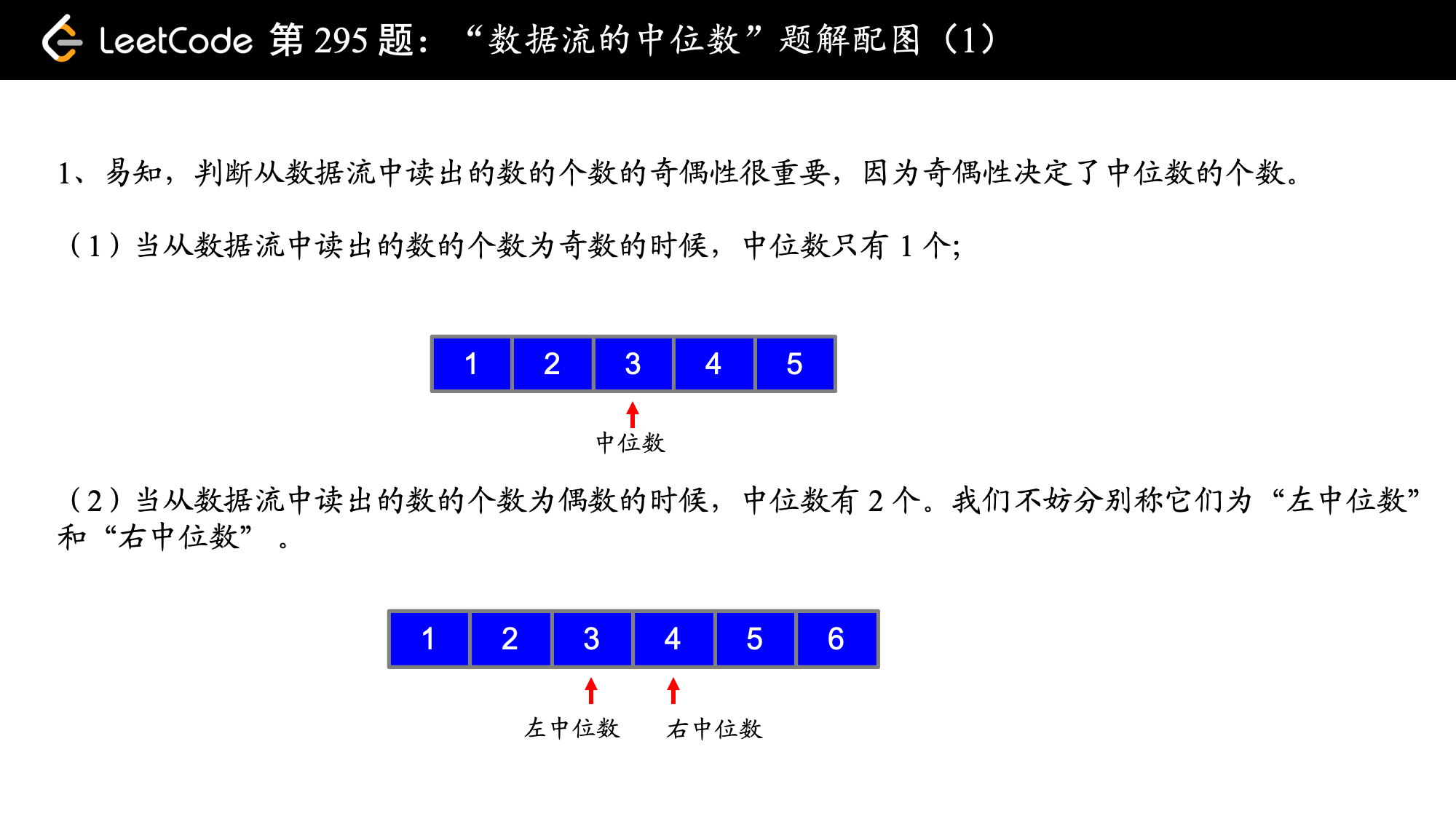
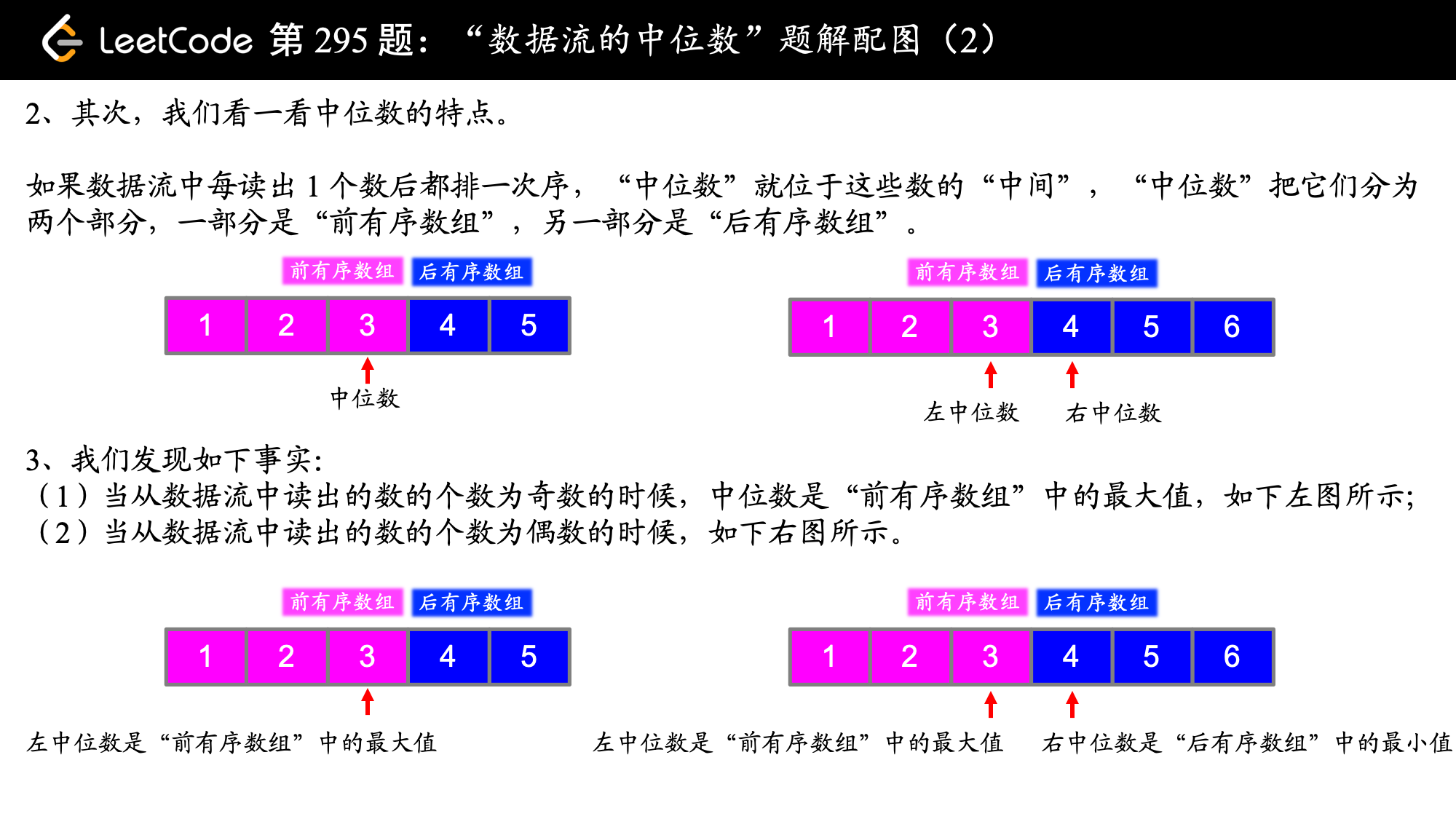
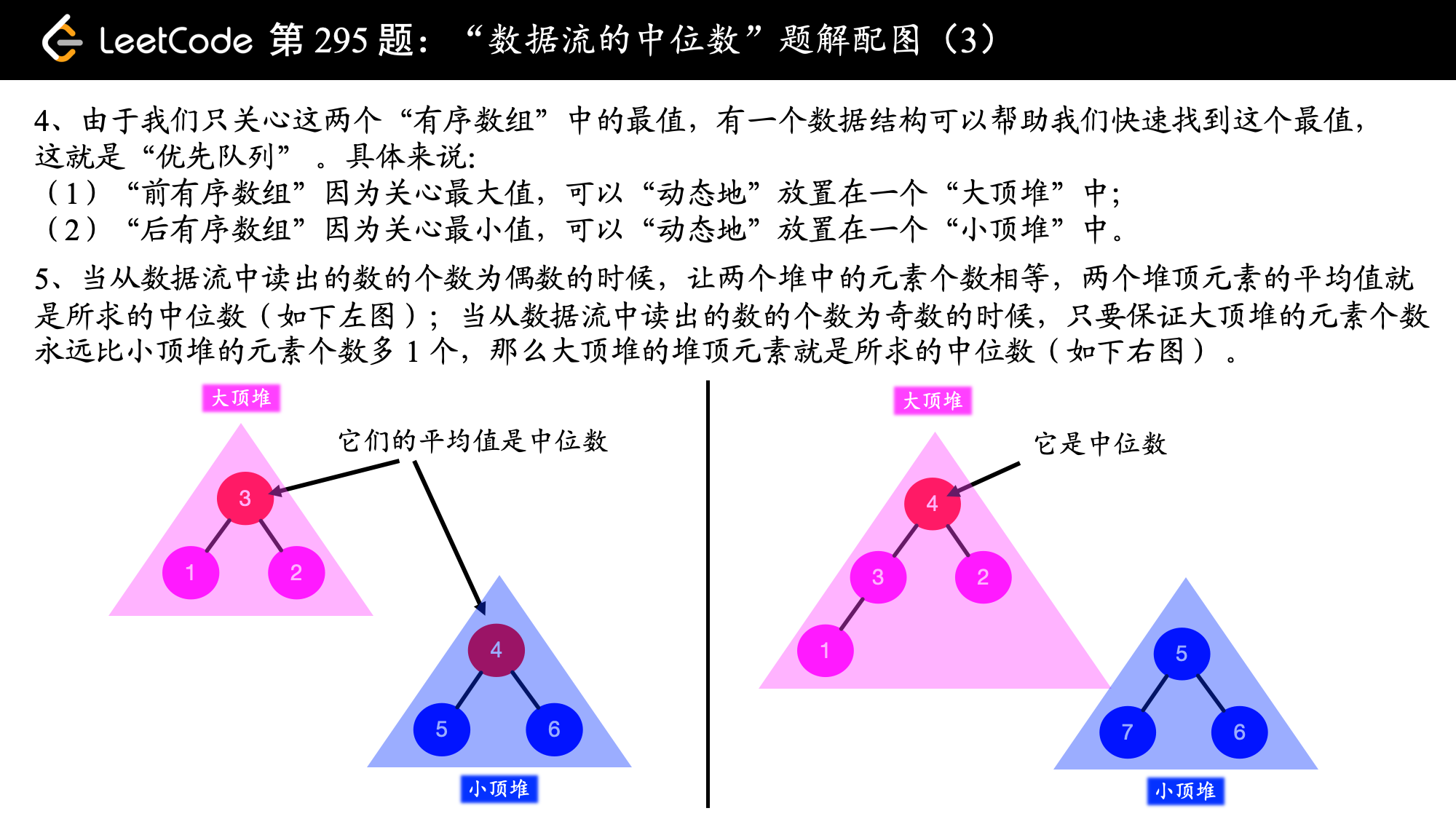

前面对于如何由该题的特点分析出需要使用堆这一数据结构讲解的非常清晰。使用两个堆,分别维护前半个有序序列的最大值(大顶堆)和后半个有序序列的最小值(小顶堆),并始终保证:
这是本题的核心。但是如何实现以确保以上这两点始终成立,在addNum()部分参考了官方题解的实现,该函数的实现还是很有技巧性的,以至于第二遍做的时候还是不会~~~
时间复杂度分析,堆结构插入一个元素需要O(log n)的时间复杂度,在addNum()中,最多需要3次插入堆的操作;而读取堆顶元素的时间复杂度是O(1),因此总的时间复杂度是O(log n);空间复杂度是O(n),即需要n个空间来存储这n个元素。
class MedianFinder {
private PriorityQueue<Integer> minHeap; // 小顶堆
private PriorityQueue<Integer> maxHeap; // 大顶堆
public MedianFinder() {
minHeap = new PriorityQueue<>();
//也可以写成 new PriorityQueue<>(Comparator.reverseOrder());
maxHeap = new PriorityQueue<>((x, y) -> y - x);//lambda表达式的写法
}
public void addNum(int num) {
maxHeap.add(num);
minHeap.add(maxHeap.poll());
if(maxHeap.size() < minHeap.size()){
maxHeap.add(minHeap.poll());
}
}
public double findMedian() {
if(maxHeap.size() == minHeap.size())
return (double)(maxHeap.peek() + minHeap.peek()) * 0.5;
else
return (double)maxHeap.peek();
}
}
思考follow up的两个问题 (参考这里)
We can maintain an integer array of length 100 to store the count of each number along with a total count. Then, we can iterate over the array to find the middle value to get our median. 去做一下这一题1093. 大样本统计关于计数排序(桶排序)的运用
Time and space complexity would be O(100) = O(1).
In this case, we need an integer array of length 100 and a hashmap for these numbers that are not in [0,100].
设计一个找到数据流中第K大元素的类(class)。注意是排序后的第K大元素,不是第K个不同的元素。可以假设 nums 的长度≥ k-1 且k ≥ 1。
评注:本题的api设计的比较奇怪,不是那么直观。
示例:
int k = 3;
int[] arr = [4,5,8,2];
KthLargest kthLargest = new KthLargest(3, arr);
kthLargest.add(3);? ?// returns 4
kthLargest.add(5);? ?// returns 5
kthLargest.add(10);? // returns 5
kthLargest.add(9);? ?// returns 8
kthLargest.add(4);? ?// returns 8
解释:
初始数组是 [4,5,8,2] ,要求数据流中第 3 大的元素
原始数组经过排序后:[8,5,4,3] -> 第3大的元素是 4
插入3 :[8,5,4,3,3] -> 第3大的元素是 4
插入5 :[8,5,5,4,3,3] -> 第3大的元素是 5
插入10 :[10,8,5,5,4,3,3] -> 第3大的元素是 5
...
分析:有了第295题的理解,再来做这一题就比较容易了。维护一个最小堆,限制堆的元素个数不超过k个。如果当前堆中的元素个数小于k个,那么可以往堆中添加元素;否则,如果待插入的元素值大于堆顶元素,则弹出堆顶元素再插入新值;如果待插入的元素小于或等于堆顶元素,则直接丢弃该元素。通过维护元素个数始终保持为k个,堆顶元素则动态的表示当前数据流第k大的元素。
class KthLargest {
private PriorityQueue<Integer> minHeap = new PriorityQueue<>();
private int K ;
public KthLargest(int k, int[] nums) {
K = k;
for(int val : nums){
add(val);
}
}
public int add(int val) {
if(minHeap.size() < K){
minHeap.add(val);
}else if(minHeap.peek() < val){
minHeap.poll();
minHeap.add(val);
}
return minHeap.peek();
}
}
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。比如,输入: [3,2,3,1,2,4,5,5,6] 和 k = 4;输出: 4。
分析:一趟扫描数组,维护一个大小为k的小顶堆,和703. 数据流中的第K大元素 的处理方式一样。
// 时间复杂度:O(n*logk)
// 空间复杂度:O(k)
class Solution {
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
for(int num : nums){
if(minHeap.size() < k){
minHeap.add(num);
}else if(num > minHeap.peek()){
minHeap.poll();
minHeap.add(num);
}
}
return minHeap.peek();
}
}
给定一个非空的整数数组,返回其中出现频率前?k?高的元素。可以假设给定的?k?总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。算法的时间复杂度必须优于 O(n log n) ,?n?是数组的大小。
示例
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
分析:本题用到了Map.Entry遍历,不熟悉,参考这里(https://www.javacodeexamples.com/iterate-through-java-hashmap-example/112)
// 时间复杂度:O(n*log(k))
// 空间复杂度:O(n)
class Solution {
public List<Integer> topKFrequent(int[] nums, int k) {
// key存放的是元素值,value存放的是元素个数
Map<Integer, Integer> map = new HashMap<>();
// 根据Map.Entry的value建立最小堆
PriorityQueue<Map.Entry<Integer, Integer>>
minHeap = new PriorityQueue<>((x,y)->(x.getValue() - y.getValue()));
for(int num : nums) { // O(n)
map.put(num, map.getOrDefault(num, 0) + 1);
}
// 核心逻辑,这里和第215题、第703题都是一样的
for(Map.Entry<Integer, Integer> entry : map.entrySet()) { // O(n)
if(minHeap.size() < k) {
minHeap.add(entry);
}else if(entry.getValue() > minHeap.peek().getValue()){
minHeap.poll();
minHeap.add(entry); // O(log(k))
}
}
List<Integer> result = new LinkedList<>();
while (!minHeap.isEmpty()) {
Map.Entry<Integer, Integer> entry = minHeap.poll();
result.add(0, entry.getKey());
}
return result;
}
}
给定一个数组 nums,有一个大小为?k?的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k?个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。可以假设 k 总是有效的,在输入数组不为空的情况下,1 ≤ k ≤?输入数组的大小。
进阶:你能在线性时间复杂度内解决此题吗?
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
---
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
分析:
// 暴力法,
// 时间复杂度:O(n*k)
// 空间复杂度:O(n-k+1)
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
if (n * k == 0) return new int[0];// 特判,根据测试用例才想到的
int[] res = new int[n - k + 1];
for (int i = 0; i < n - k + 1; i++) {// O(n)
int max = nums[i];
for (int j = i; j < i + k; j++) {// O(k)
max = Math.max(max, nums[j]);
}
res[i] = max;
}
return res;
}
}
// 借助大顶堆(优先队列)实现
// 时间复杂度:O(n*log(k))
// 空间复杂度:O(n-k+1)
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
if (k * n == 0) return new int[0];
int[] res = new int[n - k + 1];
int len = 0;
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((x, y) -> (y - x));
for (int i = 0; i < n; i++) { // O(n)
if (maxHeap.size() < k - 1) {
maxHeap.add(nums[i]);
} else {
maxHeap.add(nums[i]); // O(log(k))
res[len++] = maxHeap.peek(); // O(1)
maxHeap.remove(nums[i - k + 1]); // O(log(k))
}
}
return res;
}
}
如何在线性时间内完成,参考Java O(n) solution using deque with explanation 。第一次遇见sliding window的做法,非常巧妙。这里的复杂度分析要注意,因为每个元素只进出deque一次,因此为O(n)。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
if (k * n == 0) return new int[0];
int[] res = new int[n - k + 1];
Deque<Integer> deque = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
int start = i - k + 1; // 滑动窗口的左边界
// 窗口范围是[start, i], 移除该范围之外的元素
// 这保证了deque内始终维持着至多为k个元素
// 注意,是至多为k个,而不是始终为k个!
if (!deque.isEmpty() && deque.peekFirst() < start) {
deque.pollFirst();
}
// 随着窗口向右滑动,如果新加入的元素大于等于当前窗口范围内的其他的元素
// 很显然,先前那些元素已经没有机会成为该窗口的最大值,于是把他们删除
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
// deque存放索引
deque.add(i);
if (start >= 0) {
res[start] = nums[deque.peekFirst()];
}
}
return res;
}
}
标签:art 解决 大于 ace shm source while 中间 china
原文地址:https://www.cnblogs.com/kkbill/p/13028205.html