标签:基础 show 约束 自己 lse 出现 输入 最大 pdf
具体内容:利用Opencv对图像像素进行操作,就算归一化直方图,并在窗口以图形的方式展示出来。
具体内容:通过计算归一化的直方图,设计算法实现直方图均衡化的处理。
具体内容:在灰度图像直方图均衡化的基础上实现彩色图像直方图均衡化的处理。
对于输入像素点r和输出像素点s都在灰度级 [0,L-1]之间,r = 0 代表黑色, r = L - 1代表白色。对于r和s的变换形式为:
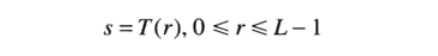
r和s满足一下条件:
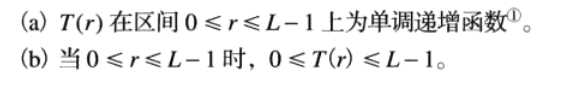
利用反函数来从s推r时,有以下定义:
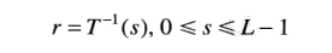
r和s满足条件:
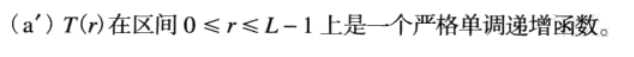
条件a是为了保证输出的灰度级不少于输入,这是为了防止二义性。条件b是为了保证输出的灰度范围和输入的灰度范围相同。条件a`也是为了保证s到r 也是一一对应的,防止二义性。实验中采用8bit整性的像素分布,不一定满足这个情况。
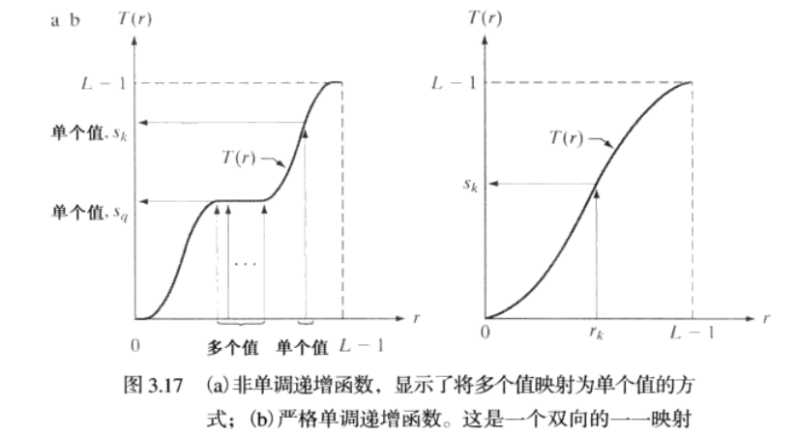
在实验中会类似左边的图像,出现多个输入的r,输出同一个s值。而在理论的约束上应该和右图相似,r与s一一对应。
对于一副灰度图像,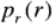
和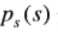
分别代表输入图像和输出图像的像素点的概率分布,我们简称为PDF。对于已知的和满足公式:
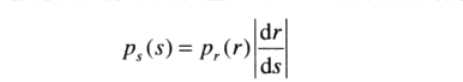
(1)
直方图均衡化的采用的公式如下:
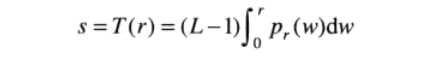
(2)
其中w是积分假变量,L-1是最大的灰度级。
为什么要这么做呢。由莱布尼兹准则,我们知道上限的定积分的导数是被积函数在该上限的值。
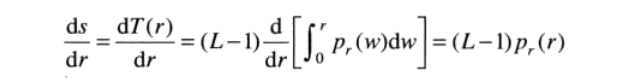
(3)
我们将的结果带入(1)中,
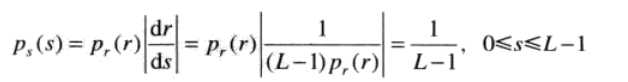
(4)
使用(2)公式后,输出图像的像素点s分布是均匀的,PDF为1/(L-1)。
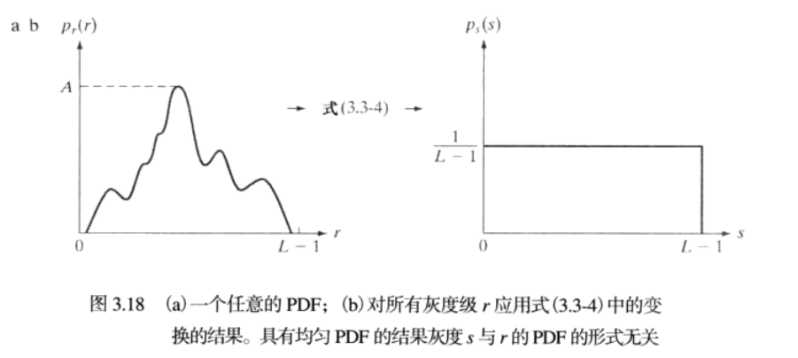
对于离散的直方图均衡化采用的公式为:
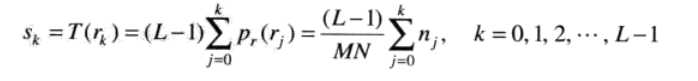
(5)
其中MN是总的像素点个数
void calHistInfo(const Mat& src, vector<unsigned int>& calVec, vector<unsigned int >& calVecBefor,unsigned int LMax){
int width = src.cols;
int height = src.rows;
int piexl = 0;
for (int h = 0; h < height; h++)
{
for (int w = 0; w < width; w++) {
piexl = (int)src.at<uchar>(h, w);
calVec[round(piexl)] += 1;
}
}
calVecBefor[0] = calVec[0];
for (int i = 1; i < calVec.size(); i++)
{
calVecBefor[i] = calVecBefor[i - 1] + calVec[i];
}
cout << "统计完毕" << endl;
}
这里我用了两个vector数组calVec 和calVecBefor ,calVec是用于记录每个灰度级别的像素个数,
calVecBefor是记录在当前像素r个数和r之前的像素之和。LMax是用于记录有多少个灰度级别,这里LMax =256。
void showHistChart(Mat& canvas,unsigned int LMax,vector<unsigned int> calVec,Scalar sca, int thikness)
{
//横轴是灰度级
//纵轴是像素的分布情况,我采取的方法是像素数目最多的为单位1
int canvas_height = canvas.rows;
int canvas_step = canvas.cols / LMax;
auto it = max_element(calVec.begin(), calVec.end());
unsigned int calMax = *it;
//开始画折线图
for (int i = 0; i < LMax-1; i++)
{
line(canvas, Point(i * canvas_step, canvas_height - (canvas_height*(1.0)*calVec[i]/calMax)),
Point((i + 1) * canvas_step, canvas_height - (canvas_height * (1.0) * calVec[i+1] / calMax)),
sca, thikness, 8);
}
}
其中canvas是画布,首先要找到像素点最多的灰度级别和该级别像素的个数calMax,以及根据画布大小和灰度级个数确定步长canvas_step,sca是画折线使用的颜色, thikness是折线的粗细,参数8是渲染方式。
void createRSTable(const vector<unsigned int>& calVecBefor,
unordered_map<unsigned int,unsigned int>& table_rs,unsigned int LMax)
{
double total = (double)calVecBefor[LMax - 1];
for (int i =0;i<LMax;i++)
{
double s = LMax*(double)calVecBefor[i] * (1.0) / total;
if (round(s) <= 255) {
table_rs.insert(make_pair(i, round(s)));
}
else
{
table_rs.insert(make_pair(i, 255));
}
}
}
这里我采用的unordered_map用于记录输入的r与输出的s之间的映射关系。当然这里也可以用数组之类的记录,记录方法就是公式(5)。
void iHistImp(Mat& src, Mat&dst, unordered_map<unsigned int,unsigned int>& table_rs) {
dst = Mat::zeros(src.size(), src.type());
int width = src.cols;
int height = src.rows;
int piexl = 0;
for (int h = 0; h < height; h++)
{
for (int w = 0; w < width; w++) {
piexl = (int)src.at<uchar>(h, w);
auto it = table_rs.find(piexl);
if (it != table_rs.end())
{
dst.at<uchar>(h, w) = it->second;
}
}
}
}
这里通过遍历灰度输入的输入像素点r,来找到相应的输出s。
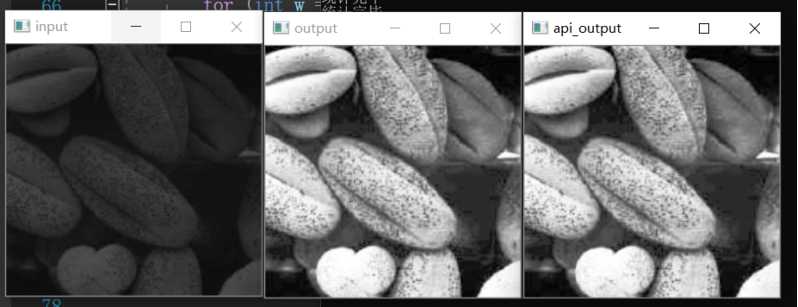
这里我除了使用自己实现的直方图均衡化,还调用opencv中直方图均衡化的api,来对比实验效果。
实验前后的折线图:
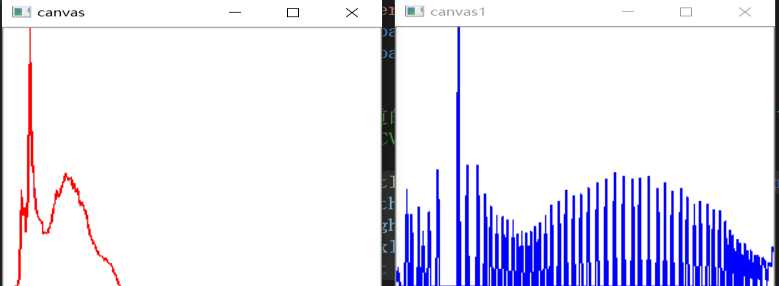
红色是直方图均衡化前的像素统计,蓝色是均衡化后的像素统计。
彩色图像的直方图均衡化,我是将输入的彩色图像分成bgr三个通道,分别进行直方图均衡化,然后再将结果合并再一起。
/*
* 彩色图像的直方图均衡化
*/
void BGRHist(Mat& src, Mat& dst)
{
//将彩色图像的按照BGR三个通道切分
vector<Mat> splitMat;
split(src,splitMat);
//分别对bgr 三个通道进行直方图均衡化
vector<Mat> mergeMat;
split(src, mergeMat);
for (int i = 0; i < 3; i++)
{
unsigned int LMax = 256;
vector<unsigned int> calVec(LMax, 0);
vector<unsigned int > calVecBefor(LMax, 0);//用于记录灰度级l之前的所以的像素点个数
calHistInfo(splitMat[i], calVec, calVecBefor, LMax);
//构建输入像素r 与输出像素s 之间的 一一映射表
unordered_map<unsigned int, unsigned int > table_rs;
createRSTable(calVecBefor, table_rs, LMax);
iHistImp(splitMat[i],mergeMat[i], table_rs);
}
merge(mergeMat,dst);
}

标签:基础 show 约束 自己 lse 出现 输入 最大 pdf
原文地址:https://www.cnblogs.com/cyssmile/p/13029676.html