放大器自激

标签：mic   公式   方法   ima   输入输出   情况   AMM   信号   mamicode   

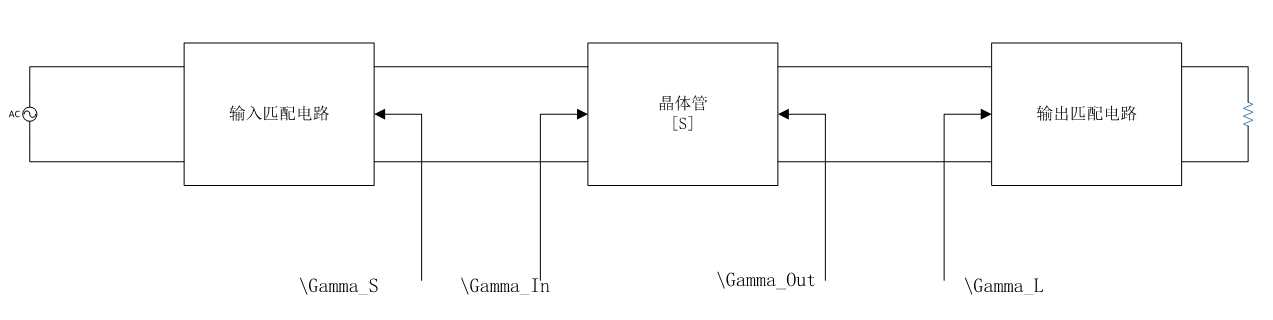
参照上图，放大器的稳定性条件分成两种：

• 无条件稳定：假如对所有无源信号源和负载阻抗，有\(|\Gamma_{in}|<1\)和\(|\Gamma_{out}|<1\)，[即\(|\Gamma_{s}|<1\)和\(\Gamma_L < 1\)]，则这个网络是无条件稳定的。
• 条件稳定：假如只对某些确定范围的无源信号源和负载阻抗，有\(|\Gamma_{in}|<1\)和$ |\Gamma_{out}|<1$，则这个网络是条件稳定的。这种情况也称为潜在的不稳定。

根据以上两个方程可以进行转化得到

以负载阻抗为例，可以将临界状态下|\(\Gamma_L = 1\)|（\(\Gamma_L\)与\(\Gamma_{in}\)的输入输出阻抗对调，所以大小相等，符号相反）表达出来，结果是一个圆。表达式为

其中，\(\Delta = S_{11}S_{22} - S_{12}S_{21}\)利用极坐标关系可知其圆心和半径位置。

如果仍然只考虑输出阻抗一边的稳定性，可以看\(\Gamma_L = 0\)的点，也就是史密斯圆图的圆心是在阻抗稳定性圆内还是圆外。如果根据稳定性判别条件，已知\(\Gamma_L = 0\)，那么只需要判断输入端口的反射系数，也就是\(|\Gamma_{in}|\)的情况。根据公式(1)，$\Gamma_L =0 \(，那么\)|\Gamma_{in}| = |S_{11}|\(。也就是说只要\)| S_{11}<1 |\(（这也可以说是\)S11$的定义了，终端匹配情况下的反射系数值），那么此时圆心就处在稳定性圆内，否则则处在稳定性圆外。

对于无条件稳定的情况，可以使用\(K-\Delta\)检验的方法进行值得检验，或者更简单的使用\(\mu\)检验。对于\(\mu\)检验，只要根据S矩阵判断下面的值，就可以得到

如果\(\mu > 1\)，则意味着该器件无条件稳定，而且\(\mu\)值越大，器件的稳定性越高。

放大器自激

标签：mic   公式   方法   ima   输入输出   情况   AMM   信号   mamicode   

原文地址：https://www.cnblogs.com/lafiizh/p/13034728.html