标签：pre   out   大小   集合   space   图片   math   tps   pen   

题目描述

prufer序

最近的数学题有些多啊

不是pufer也不是puffer

用来求有标号无根生成树个数

构建：每次把当前度数为1的标号最小的点删掉，把其连着的点写下来，直到剩下两个点

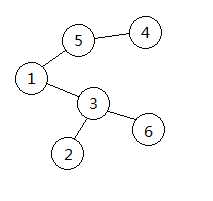
如图的prufer序为3513

还原：设点集V={1..n}，按顺序把prufer序中的数和点集中不在当前prufer序的数连边，并把这两个数分别在对应的集合里删掉，最后把剩下的两个连起来

如上图，第一次不在的是2，连2-3，第二次是4，连4-5，第三次是5，连5-1，第四次是1，连1-3，最后连3-6

其实就是找当前删掉的点连边

可以发现每个prufer序对应唯一一棵树，每一位是1~n共n-2位，所以生成树个数是n^(n-2)

有若干边已选的情况

设剩余m块，每块大小为ai

把每块视作一个点，连边仍然和原本的点连边，最后剩下的两块互相连，那么有n^(m-2)种连法

但是这样没有考虑块内具体是哪个点连的，所以要乘上Πai

所以方案数是n^(m-2)*Πai

生成函数

一条常用的式子：\(\sum_{i>=0}{x^i}=\frac{1}{1-x}\)

证明：设\(S=\sum_{i>=0}{x^i}\)，则\(xS=\sum_{i>=1}{x^i}\)

有\((1-x)S=1\)，即\(\frac{1}{1-x}=S=\sum_{i>=0}{x^i}\)

因此有\(\frac{1}{(1-x)^m}=\sum{\binom{i+m-1}{m-1}x^i}\)

题解

597tql：https://www.cnblogs.com/jz-597/p/13027755.html

先求至少k条边的方案f(k)

块数m=n-k，则f(k)=n^(m-2)*Σ所有方案的Πai

则\(f(k)=n^{m-2}*[x^n](\sum{ix^i})^m\)

因为\(\frac{1}{(1-x)^2}=\sum{\binom{i+1}{1}x^i}=\sum{(i+1)x^i}\)，\(\frac{x}{(1-x)^2}=\sum_{i>=1}{ix^i}\)

所以\(f(k)=n^{m-2}*[x^n]\frac{x^m}{(1-x)^{2m}}=n^{m-2}*[x^{n-m}]\frac{1}{(1-x)^{2m}}=n^{m-2}*\binom{n+m-1}{n-m}\)

可以二项式反演+NTT求g(k)，但没必要

考虑如果贡献是2^k，那么g(k)会在f(i)（i<=k）处算C(k,i)次，加起来刚好是2^k

因此\(ans=\sum g(i)*2^i=\sum f(i)\)

现在贡献是k*2^k，有这样一条式子：

\(\sum{i\binom{k}{i}}=k*2^{k-1}\)，证明见https://www.cnblogs.com/gmh77/p/11482696.html

所以\(\sum f(i)*i=\sum g(k)*\sum i{\binom{k}{i}}=\sum g(k)*k*2^{k-1}=ans/2\)

时间O(n)

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define C(n,m) (jc[n]*Jc[m]%998244353*Jc[(n)-(m)]%998244353)
#define mod 998244353
#define Mod 998244351
#define ll long long
#define file
using namespace std;

ll jc[1000001],Jc[1000001],w[1000001],f[500001],p[500001],ans;
int n,m,i,j,k,l;

ll qpower(ll a,int b) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}

int main()
{
	freopen("traffic.in","r",stdin);
	#ifdef file
	freopen("traffic.out","w",stdout);
	#endif
	
	scanf("%d",&n);
	jc[0]=jc[1]=Jc[0]=Jc[1]=w[1]=1;
	fo(i,2,n+n) w[i]=mod-w[mod%i]*(mod/i)%mod,jc[i]=jc[i-1]*i%mod,Jc[i]=Jc[i-1]*w[i]%mod;
	p[0]=1;
	fo(i,1,n) p[i]=p[i-1]*n%mod;
	
	fo(i,0,n-2) m=n-i,f[i]=C(n+m-1,n-m)*p[m-2]%mod;f[n-1]=1;
	fo(i,0,n-1) ans=(ans+f[i]*i)%mod;
	printf("%lld\n",ans*2%mod);
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}

6675. 【2020.05.30省选模拟】交通网络（prufer序、常用生成函数）

标签：pre   out   大小   集合   space   图片   math   tps   pen   

原文地址：https://www.cnblogs.com/gmh77/p/13039671.html