标签:获取 const 子节点 排列 查找树 sed ring min 核心
给定n个圆的半径序列,将它们放到矩形框中,各圆与矩形底边相切,求具有最小排列长度的圆排列。
根据示例:
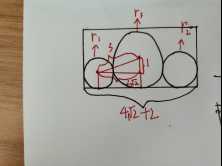
可得两个圆之间的距离计算为:sqrt((r1+r3)2-(r1-r3)2),即 2*sqrt(r1*r3)
由于当前的圆不一定恰好与它前面的圆相切,故我们可以通过计算当前圆与其前面所有圆的距离,得到的最大结果即当前圆的横坐标值。
搜索树:叶子节点即所有结果集
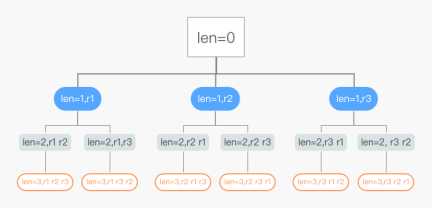
设计
计算方法:
核心伪代码

1 double calCircleCenter(int n){//计算圆心坐标 2 for(int i=1;i<n;i++){ 3 因为当前该圆可能与排在其前面的所有圆相切 4 所以需要逐个计算与不同圆相切的情况。 5 } 6 返回圆心横坐标值 7 } 8 9 void calCircleSortLength(){//计算圆排列的总长度 10 double low=99999,high=0; 11 for(int i=1;i<=CIRCLENUM;i++){ 12 //分别找出改序列的起点值与终点值 13 //该问题可以抽象成找出圆的横坐标减去其半径值,通过遍历所有圆,找出计算结果最小的,即第一个圆。而终点值即最后一个圆的横坐标值加上其半径值,得到的最大结果即该圆序列的终点值。 14 if(x[i]-r[i]<low){ 15 low=x[i]-r[i]; 16 } 17 if(x[i]+r[i]>high){ 18 high=x[i]+r[i]; 19 } 20 } 21 if(high-low<minLen){ 22 minLen=high-low; 23 for(int i=1;i<=CIRCLENUM;i++){//保存当前的最短圆序列 24 circleSeq[i]=r[i]; 25 } 26 } 27 } 28 29 30 void findCircleSort(int n){ //查找圆排列 31 if(n==CIRCLENUM+1){ 32 //若已经搜索完查找树的最后一层,说明已经形成一个结果 33 可以计算该结果的圆序列长度 34 calCircleSortLength(); 35 } 36 for(int i=n;i<=CIRCLENUM;i++){//搜索所有可能性的结果 37 swap(r[n],r[i]); 38 double center=calCircleCenter(n);//获取圆当前的横坐标 39 x[n]=center; 40 findCircleSort(n+1);//向下继续搜索 41 swap(r[n],r[i]);//回溯 42 } 43 }
实现代码

1 // 2 // main.cpp 3 // circleSort 4 // 5 // Created by yizhihenpidehou on 2020/6/4. 6 // Copyright © 2020 yizhihenpidehou. All rights reserved. 7 // 8 9 #include <iostream> 10 #include <algorithm> 11 #include <stdio.h> 12 #include <string.h> 13 #include <cmath> 14 using namespace std; 15 const int CIRCLENUM =3; 16 double x[200];//存放每个圆的x轴位置 17 double r[200];//存放每个圆的半径 18 double circleSeq[200];//存放最短圆序列的半径 19 int minLen=999999;//存放最短圆排列长度 20 double calCircleCenter(int n){//计算圆心坐标 21 double maxx=0; 22 for(int i=1;i<n;i++){ 23 int num=x[i]+2.0*sqrt(r[i]*r[n]); 24 if(num>maxx){ 25 maxx=num; 26 } 27 } 28 return maxx; 29 } 30 void calCircleSortLength(){//计算圆排列的总长度 31 double low=99999,high=0; 32 for(int i=1;i<=CIRCLENUM;i++){ 33 if(x[i]-r[i]<low){ 34 low=x[i]-r[i]; 35 } 36 if(x[i]+r[i]>high){ 37 high=x[i]+r[i]; 38 } 39 } 40 if(high-low<minLen){ 41 minLen=high-low; 42 //printf("输出最短圆序列\n"); 43 for(int i=1;i<=CIRCLENUM;i++){ 44 circleSeq[i]=r[i]; 45 } 46 // printf("\n"); 47 } 48 } 49 void findCircleSort(int n){ //查找圆排列 50 if(n==CIRCLENUM+1){ 51 calCircleSortLength(); 52 } 53 for(int i=n;i<=CIRCLENUM;i++){ 54 swap(r[n],r[i]); 55 double center=calCircleCenter(n);//获取圆当前的横坐标 56 x[n]=center; 57 findCircleSort(n+1);//向下继续搜索 58 swap(r[n],r[i]);//回溯 59 } 60 } 61 int main(int argc, const char * argv[]) { 62 r[1]=1;r[2]=1;r[3]=2;//初始化半径 63 findCircleSort(1); 64 printf("最短圆序列:\n"); 65 for(int i=1;i<=CIRCLENUM;i++){//输出最短圆序列 66 printf("%f ",circleSeq[i]); 67 } 68 printf("\n"); 69 return 0; 70 }
因为根据不同的排列方法取最小长度的圆排列,所以根据全排列公式要进行n!次查找,由于每次完成一个结果集后,还要找到起点值与终点值,即需要O((n+1)!)的时间复杂度
空间复杂度为O(n),因为该算法中只用到几个一维数组
标签:获取 const 子节点 排列 查找树 sed ring min 核心
原文地址:https://www.cnblogs.com/pipihoudewo/p/13049017.html