标签:颜色 因此 res 理解 load ali 变换 静态 exp
语谱图就是语音频谱图,一般是通过处理接收的时域信号得到频谱图,因此只要有足够时间长度的时域信号就可。专业点讲,那是频谱分析视图,如果针对语音数据的话,叫语谱图。语谱图的横坐标是时间,纵坐标是频率,坐标点值为语音数据能量。由于是采用二维平面表达三维信息,所以能量值的大小是通过颜色来表示的,颜色深,表示该点的语音能量越强。
为了更清楚的理解语谱图,我们分四步走:
看时域图
看频域图
看时域图与频域图的关系
看语谱图
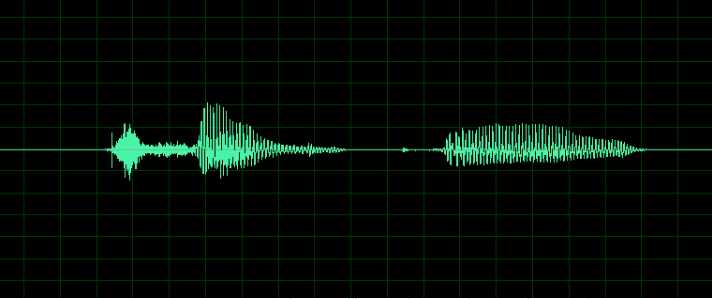
自变量是时间,即横轴是时间,纵轴是信号的变化(振幅)。其动态信号x(t)是描述信号在不同时刻取值的函数。
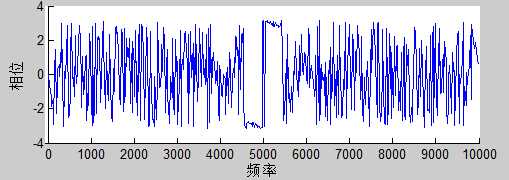
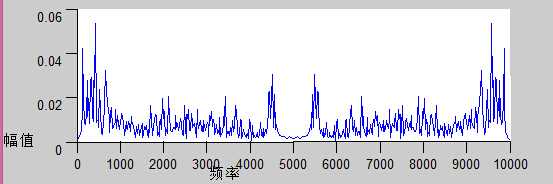
简单地说,任何信号(当然要满足一定的数学条件,但是说多了又不好懂了,所以先不提),都可以通过傅立叶变换而分解成一个直流分量(也就是一个常数)和若干个(一般是无穷多个)正弦信号的和。每个正弦分量都有自己的频率和幅值,这样,以频率值作横轴,以幅值作纵轴,把上述若干个正弦信号的幅值画在其所对应的频率上,就做出了信号的幅频分布图,也就是所谓频谱图 ,另外还有相频分布 。
如下面静态图所示,正弦波就是一个圆周运动在一条直线上的投影。如下面动图所示,频域的基本单元也可以理解为一个始终在旋转的圆。
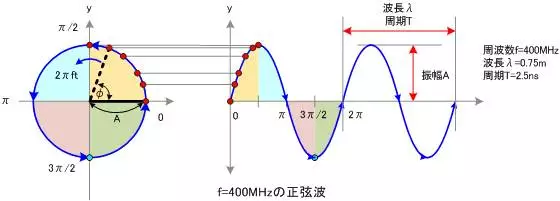
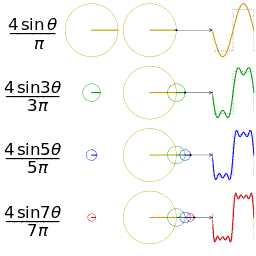
下图为任意一个波形在时域和频域的关系:
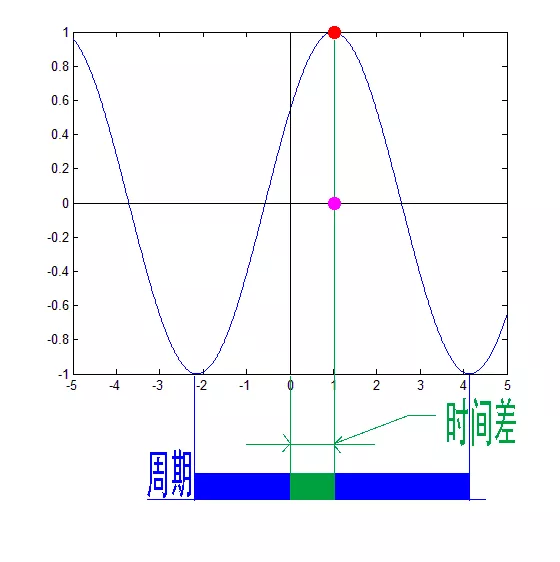
图中, 小红点是距离频率轴最近的波峰, 我们将红色的点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。时间差并不是相位差。如果将全部周期看作2Π或者360度的话,相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘 2Π,就得到了相位差。
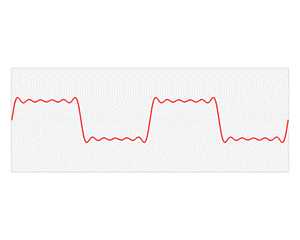
最后,总结一下,下图为一个矩形波在时域、频域和相位的表现形式:
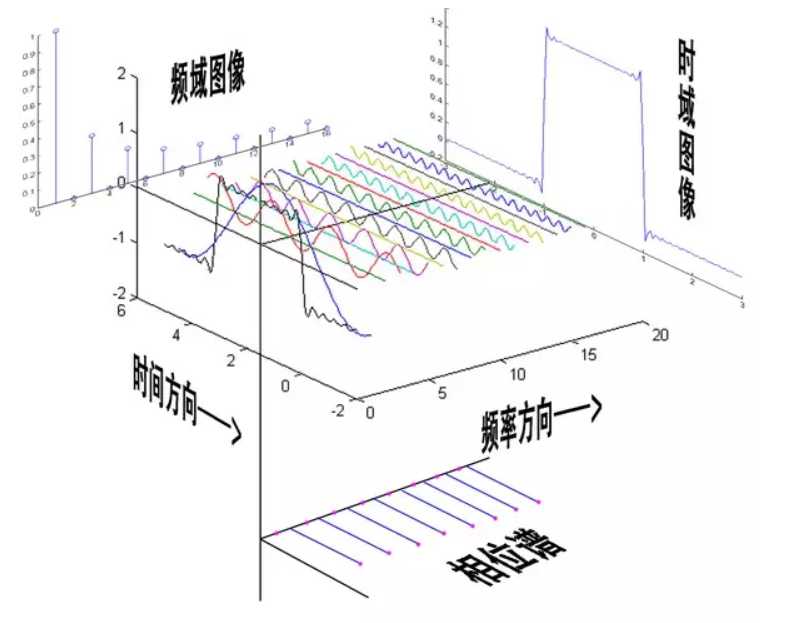
注:其中一系列正弦波形合成一个时域的矩形波,而当中的横穿它们的黑线为我们作相位谱的频率轴。
对于一段语音信号x(t),
首先分帧,变为x(m,n)(m为帧的个数,n为帧长);
然后做FFT变换,得到X(m,n);
作周期图Y(m,n)(Y(m,n) = X(m,n) * X(m,n)T);
接着取10 log10(Y(m,n)),把m根据时间变换一下刻度M,n根据频率变化一下刻度N;
最后将(M,N, 10 log10(Y(m,n))) 画成二维图就是语谱图了。
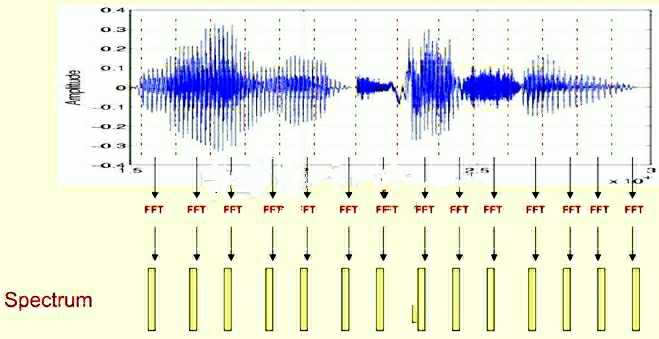
这里,这段语音被分为很多帧,每帧语音都对应于一个频谱(通过短时FFT计算),频谱表示频率与能量的关系。在实际使用中,频谱图有三种,即线性振幅谱、对数振幅谱、自功率谱 。 (对数振幅谱中各谱线的振幅都作了对数计算,所以其纵坐标的单位是dB(分贝) 。 这个变换的目的是使那些振幅较低的成分相对高振幅成分得以拉高,以便观察掩盖在低幅噪声中的周期信号)。
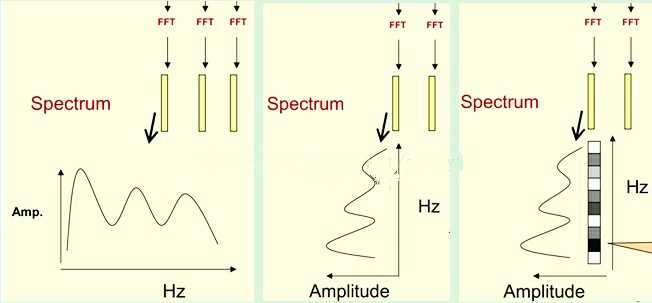
我们先将其中一帧语音的频谱通过坐标表示出来,如上图左。现在我们将左边的频谱旋转90度。得到中间的图。然后把这些幅度映射到一个灰度级表示(也可以理解为将连续的幅度量化为256个量化值),0表示黑,255表示白色。幅度值越大,相应的区域越黑。这样就得到了最右边的图。
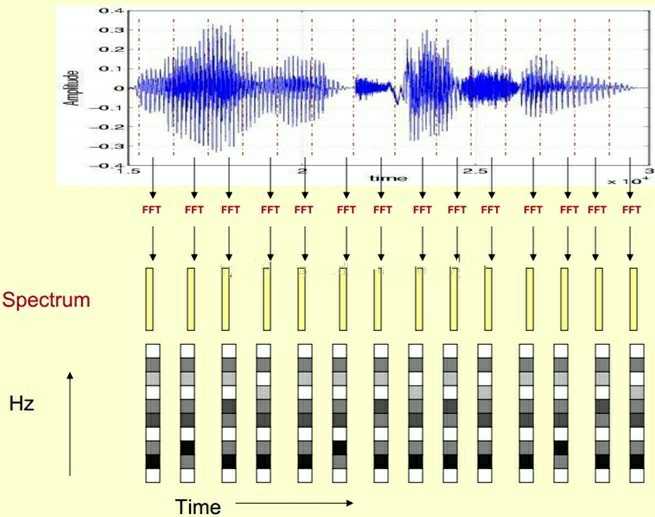
我们可以看出,之所以将其变成灰度级表示,是为了添加时间轴,让分帧的不连续性消失,起到将其用二维表示出三维的作用。
窄带语谱图
宽带语谱图
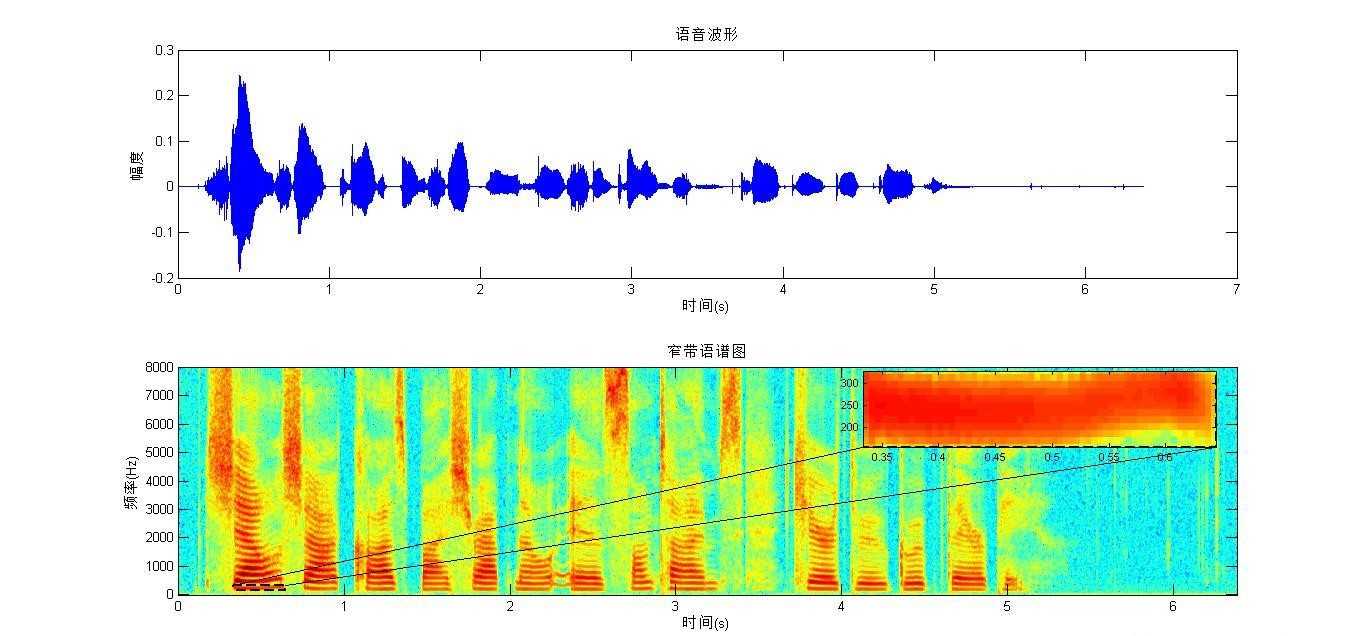
从结果图中可以清楚看到谐波的结构,频率分辨率非常好,但是时间上的分辨率就不理想,窄带语谱图,频率分辨率太过精细,不能很好体现出共振峰的大致位置,即反映不出基波的变化特性。
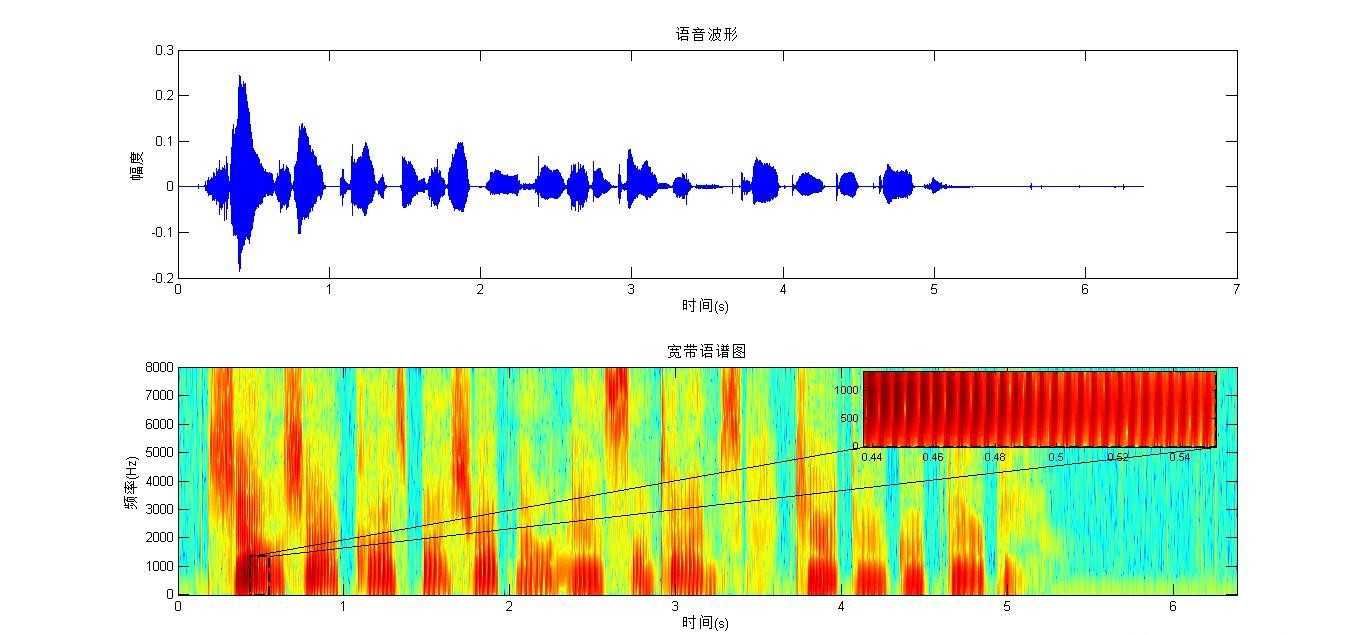
与窄带语谱图相反,宽带语谱图的时间分辨率很好,频率分辨率较低,不能很好反映声音的纹理特性,反映了频谱的时变特性,能很好分辨出共振峰的大致位置,但分辨不清谐波结构。
基音周期表示声带的震动周期,每隔这么长时间(震动周期),有一个气流通过,“每隔”就体现了周期性,这就是基音周期,那么谱图上就应该有这个频率的信号分量,而且这个频率的幅度(能量)不应该很小,因为每隔一段时间“就有”一团能量通过声带。所以基音频率所在的成分在窄带语谱图上应该是所有横条纹中频率范围最低的那条。
在窄带语谱图中,用虚线框框住的部分就表示基音频率成分,与其在同一水平线上的条纹都表示该时刻的基音频率成分,这条条纹对应的纵轴刻度值就表示基音频率。从窄带语谱图的小图可估计基音频率大约在250Hz左右,基音频率略有波动,0.5s处大约是240Hz。其他横条纹就是各次谐波,这些谐波中有些地方颜色比同时刻其附近其他横条纹颜色要深,这些颜色深的条纹表示共振峰。有些时刻,颜色较局部附近深的条纹不止一条,这些深色条纹组成了各次共振峰,如第一、第二、第三共振峰。
标签:颜色 因此 res 理解 load ali 变换 静态 exp
原文地址:https://www.cnblogs.com/minyuan/p/13054113.html