标签:des style blog http io color ar os 使用
http://www.ics.uci.edu/~dramanan/teaching/ics273a_winter08/lectures/lecture14.pdf
损失函数可以看做 误差部分(loss term) + 正则化部分(regularization term)
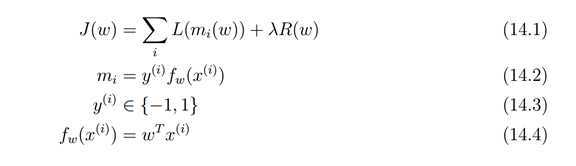
1.1 Loss Term
? ?
Gold Standard 又被称为0-1 loss, 记录分类错误的次数
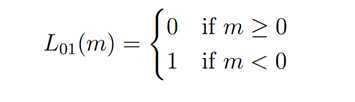
Hinge Loss http://en.wikipedia.org/wiki/Hinge_loss
For an intended output?t?= ±1?and a classifier score?y, the hinge loss of the prediction?y?is defined as
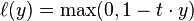
Note that?y?should be the "raw" output of the classifier‘s decision function, not the predicted class label. E.g., in linear SVMs,?
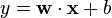
It can be seen that when?t?and?y?have the same sign (meaning?y?predicts the right class) and?
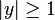
, the hinge loss?
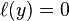
, but when they have opposite sign,?
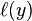
increases linearly with?y?(one-sided error).
? ?
来自 <http://en.wikipedia.org/wiki/Hinge_loss>
Plot of hinge loss (blue) vs. zero-one loss (misclassification, green:y?< 0) for?t?= 1?and variable?y. Note that the hinge loss penalizes predictions?y?< 1, corresponding to the notion of a margin in a support vector machine.
? ?
来自 <http://en.wikipedia.org/wiki/Hinge_loss>
? ?
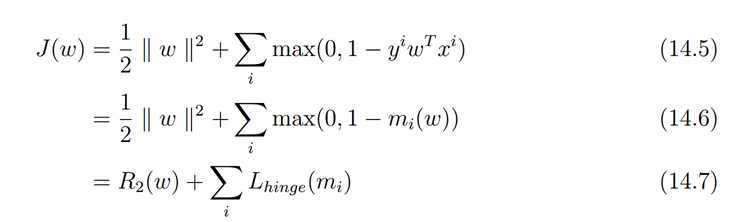
? ?
在Pegasos: Primal Estimated sub-GrAdient SOlver for SVM论文中
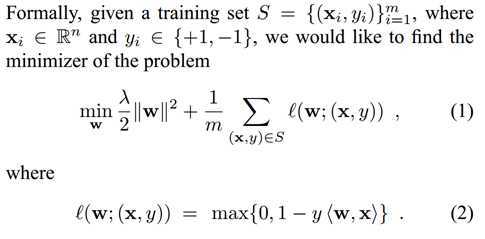
这里把第一部分看成正规化部分,第二部分看成误差部分,注意对比ng关于svm的课件
不考虑规则化
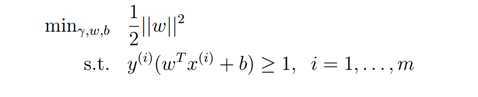
考虑规则化

? ?
Log Loss
Ng的课件1,先是讲 linear regression 然后引出最小二乘误差,之后概率角度高斯分布解释最小误差。
然后讲逻辑回归,使用MLE来引出优化目标是使得所见到的训练数据出现概率最大
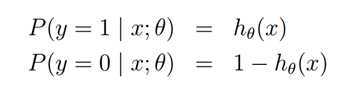
? ?
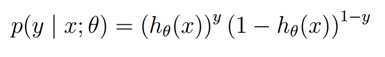
? ?
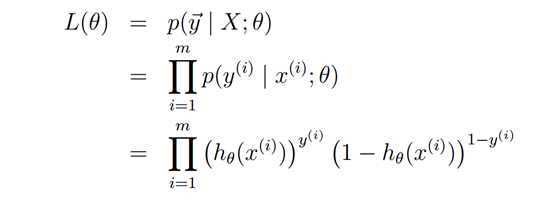
最大化下面的log似然函数
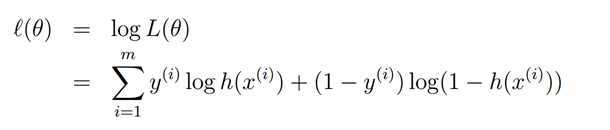
而这个恰恰就是最小化cross entropy!
? ?
http://en.wikipedia.org/wiki/Cross_entropy
http://www.cnblogs.com/rocketfan/p/3350450.html 信息论,交叉熵与KL divergence关系
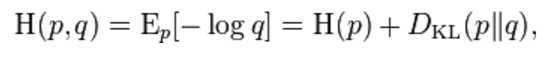

? ?
Cross entropy can be used to define loss function in machine learning and optimization. The true probability?
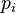
?is the true label, and the given distribution?
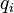
?is the predicted value of the current model.
More specifically, let us consider?logistic regression, which (in its most basic guise) deals with classifying a given set of data points into two possible classes generically labelled?
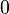
?and?

. The logistic regression model thus predicts an output?
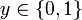
, given an input vector?
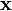
. The probability is modeled using thelogistic function?
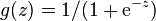
. Namely, the probability of finding the output?
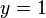
?is given by
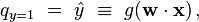
where the vector of weights?
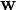
?is learned through some appropriate algorithm such as?gradient descent. Similarly, the conjugate probability of finding the output?
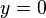
?is simply given by
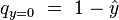
The true (observed) probabilities can be expressed similarly as?
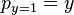
?and?
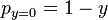
.
? ?
Having set up our notation,?
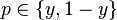
?and?
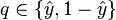
, we can use cross entropy to get a measure for similarity between?
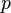
?and?
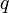
:
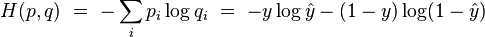
The typical loss function that one uses in logistic regression is computed by taking the average of all cross-entropies in the sample. For specifically, suppose we have?
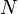
?samples with each sample labeled by?
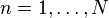
. The loss function is then given by:
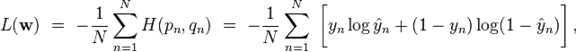
where?
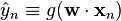
, with?
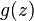
?the logistic function as before.
? ?
The logistic loss is sometimes called cross-entropy loss. It‘s also known as log loss (In this case, the binary label is often denoted by {-1,+1}).[1]
? ?
来自 <http://en.wikipedia.org/wiki/Cross_entropy>
? ?
? ?
因此和ng从MLE角度给出的结论是完全一致的! 差别是最外面的一个负号
也就是逻辑回归的优化目标函数是 交叉熵

? ?
squared loss
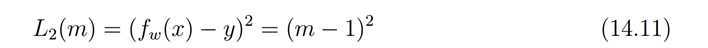
? ?
exponential loss
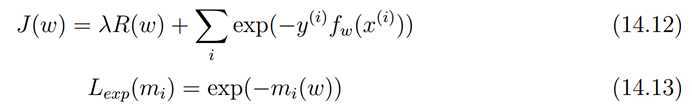
指数误差通常用在boosting中,指数误差始终> 0,但是确保越接近正确的结果误差越小,反之越大。
? ?
? ?
标签:des style blog http io color ar os 使用
原文地址:http://www.cnblogs.com/rocketfan/p/4083821.html