标签:play tin 路径 答案 namespace back queue owb front
考虑将每一列的联通块看作一个大点,相邻的联通块连边,那么将建立出一个树形结构

膜\(ywy\)神犇 借图
我们把每个具体的点称作小点,每列的联通块称作大点
两小点之间的路径可以在树上唯一地表示出来,考虑怎么计算两小点之间的路径长度
一个小点移动到另一小点,可以看作两个点在某个大点内部相遇
那么假设他们在编号为\(x\)的大点相遇,两小点之间的路径长度应该为两小点到该大点的距离加上大点内部的距离
求一个到树上标记点的最远距离,支持插入,考虑动态点分治
建出点分树,每个小点维护自己到点分树上深度为\(d\)的祖先大点的最近距离
假设一个有商店的小点距离自己的最近距离为\(dis\),与大点的连接位置为\(pos\)
那么可以维护两个树状数组,分别维护大点内部小点的前缀最小值和后缀最小值
把\(dis-pos\)插入前缀最小值的\(pos\)位置,\(dis+pos\)插入后缀最小值的\(pos\)位置
对于每个询问,设\(d\)为询问小点到该大点的距离,\(p\)为连接位置
画个图来理解别吐槽我画的丑
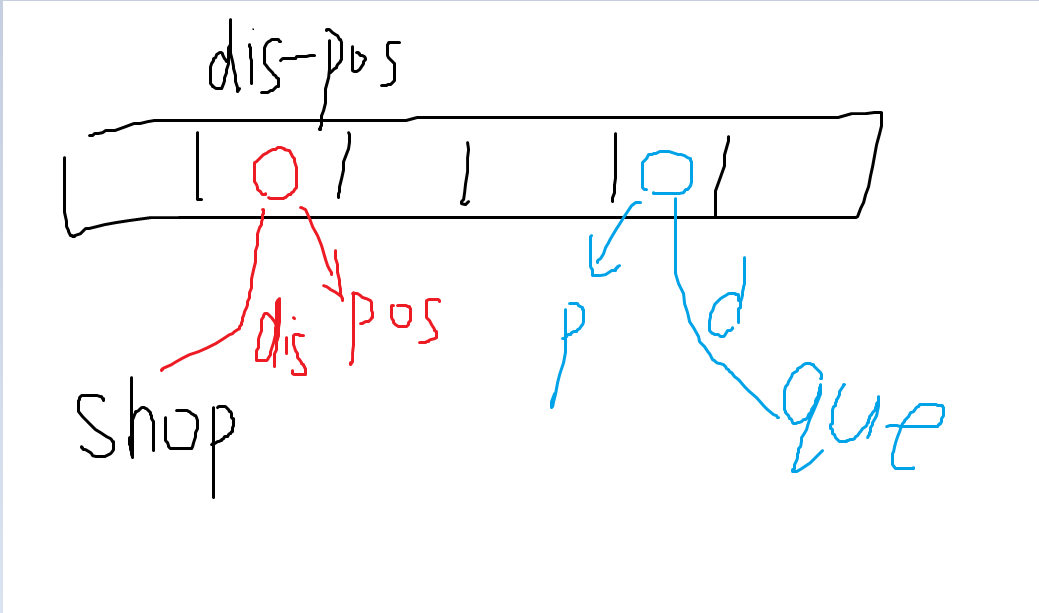
假设左侧红点是距离它最近的\(shop\)的,蓝点的询问位置,那么根据上式,这个点的答案应该是\(dis-pos+d+p\)
即两个小点到该大点的距离加上大点内部的距离
红点的值用维护前缀最小值的树状数组寻找,后缀最小值同理
#include<bits/stdc++.h>
using namespace std;
namespace red{
#define int long long
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define lowbit(i) ((i)&(-i))
inline int read()
{
int x=0;char ch,f=1;
for(ch=getchar();(ch<‘0‘||ch>‘9‘)&&ch!=‘-‘;ch=getchar());
if(ch==‘-‘) f=0,ch=getchar();
while(ch>=‘0‘&&ch<=‘9‘){x=(x<<1)+(x<<3)+ch-‘0‘;ch=getchar();}
return f?x:-x;
}
const int N=3e5+10,inf=0x3f3f3f3f;
int n,m,cnt,no,que;
int sum,rt;
int b[N],c[N],lx[N],ly[N];
int str[N],son[N],dep[N],fa[N],vis[N];
int p[N][21],dis[N][21];
vector<int> e[N],g[N],s[N],bit1[N],bit2[N];
map<int,int> id[N];
queue<int> q;
inline void linkg(int x,int y)
{
g[x].push_back(y);g[y].push_back(x);
}
inline void linke(int x,int y)
{
e[x].push_back(y);e[y].push_back(x);
}
inline void update1(int k,int x,int v)
{
for(;x<=c[k];x+=lowbit(x))
bit1[k][x]=min(bit1[k][x],v);
}
inline int query1(int k,int x)
{
int ret=inf;
for(;x;x-=lowbit(x))
ret=min(ret,bit1[k][x]);
return ret;
}
inline void update2(int k,int x,int v)
{
for(;x;x-=lowbit(x))
bit2[k][x]=min(bit2[k][x],v);
}
inline int query2(int k,int x)
{
int ret=inf;
for(;x<=c[k];x+=lowbit(x))
ret=min(ret,bit2[k][x]);
return ret;
}
inline void init()
{
for(int x=1;x<=m;++x)
{
if(s[x].empty()) continue;
sort(s[x].begin(),s[x].end());
int j=0;
for(int i=0;i<(int)s[x].size();++i)
{
int v=s[x][i];id[x][v]=++no;
if(i&&s[x][i-1]+1==v) linkg(no,no-1);
else ++cnt,lx[cnt]=x,ly[cnt]=i;
b[no]=cnt,++c[cnt];
while(j<(int)s[x-1].size()&&s[x-1][j]<v) ++j;
if(j<(int)s[x-1].size()&&s[x-1][j]==v)
{
int t=id[x-1][s[x-1][j]];
linkg(no,t);linke(cnt,b[t]);
}
}
}
for(int i=1;i<=cnt;++i)
{
sort(e[i].begin(),e[i].end());
e[i].erase(unique(e[i].begin(),e[i].end()),e[i].end());
}
for(int i=1;i<=cnt;++i)
{
for(int j=0;j<=c[i];++j)
bit1[i].push_back(inf),bit2[i].push_back(inf);
}
}
inline void getroot(int now,int fa)
{
str[now]=c[now],son[now]=0;
for(auto t:e[now])
{
if(vis[t]||t==fa) continue;
getroot(t,now);
str[now]+=str[t];
son[now]=max(son[now],str[t]);
}
son[now]=max(son[now],sum-str[now]);
if(son[now]<son[rt]) rt=now;
}
inline void build(int x,int d)
{
while(!q.empty()) q.pop();
for(int i=ly[x];i<ly[x]+c[x];++i)
{
int y=s[lx[x]][i],u=id[lx[x]][y];
p[u][d]=i-ly[x]+1;dis[u][d]=0;
q.push(u);
}
while(!q.empty())
{
int now=q.front();q.pop();
for(auto t:g[now])
{
if(vis[b[t]]||p[t][d]) continue;
p[t][d]=p[now][d],dis[t][d]=dis[now][d]+1;
q.push(t);
}
}
}
inline void solve(int now,int d)
{
vis[now]=1,dep[now]=d;build(now,d);
for(auto t:e[now])
{
if(vis[t]) continue;
rt=0,sum=str[t];
getroot(t,now);fa[rt]=now;
solve(rt,d+1);
}
}
inline void update(int x)
{
for(int y=b[x],d;y;y=fa[y])
{
d=dep[y];
update1(y,p[x][d],dis[x][d]-p[x][d]);
update2(y,p[x][d],dis[x][d]+p[x][d]);
}
}
inline int query(int x)
{
int ret=inf;
for(int y=b[x],d;y;y=fa[y])
{
d=dep[y];
ret=min(ret,min(dis[x][d]+p[x][d]+query1(y,p[x][d]),dis[x][d]-p[x][d]+query2(y,p[x][d])));
}
return ret<N?ret:-1;
}
inline void main()
{
n=read();
for(int x,y,i=1;i<=n;++i)
{
x=read(),y=read();
m=max(m,x);
s[x].push_back(y);
}
init();son[0]=sum=n;
getroot(1,0);solve(rt,0);
que=read();
for(int opt,x,y,i=1;i<=que;++i)
{
opt=read(),x=read(),y=read();
if(opt&1) update(id[x][y]);
else printf("%lld\n",query(id[x][y]));
}
}
}
signed main()
{
red::main();
return 0;
}
标签:play tin 路径 答案 namespace back queue owb front
原文地址:https://www.cnblogs.com/knife-rose/p/13059872.html