标签:除了 == 用两个 电话 owa div 返回 minus while
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
排序 + 双指针
本题的难点在于如何去除重复解。
算法流程:
特判,对于数组长度 nnn,如果数组为 nullnullnull 或者数组长度小于 333,返回 [][][]。
对数组进行排序。
遍历排序后数组:
若 nums[i]>0nums[i]>0nums[i]>0:因为已经排序好,所以后面不可能有三个数加和等于 000,直接返回结果。
对于重复元素:跳过,避免出现重复解
令左指针 L=i+1L=i+1L=i+1,右指针 R=n−1R=n-1R=n−1,当 L<RL<RL<R 时,执行循环:
当 nums[i]+nums[L]+nums[R]==0nums[i]+nums[L]+nums[R]==0nums[i]+nums[L]+nums[R]==0,执行循环,判断左界和右界是否和下一位置重复,去除重复解。并同时将 L,RL,RL,R 移到下一位置,寻找新的解
若和大于 000,说明 nums[R]nums[R]nums[R] 太大,RRR 左移
若和小于 000,说明 nums[L]nums[L]nums[L] 太小,LLL 右移
复杂度分析
时间复杂度:O(n2),数组排序 O(Nlog?N),遍历数组 O(n),双指针遍历 O(n),总体 O(Nlog?N)+O(n)∗O(n) ,O(n2)
空间复杂度:O(1)
import java.util.ArrayList;
import java.util.Arrays;
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> list = new ArrayList();
Arrays.sort(nums);
if(nums.length<3)return list;
for(int i=0;i<nums.length;i++){
if(i>0&&nums[i]==nums[i-1])continue;
int L=i+1;
int R=nums.length-1;
if(nums[i]>0)break;
while(L<R){
int sum=nums[i]+nums[L]+nums[R];
if(sum==0){
list.add(Arrays.asList(nums[i],nums[L],nums[R]));
while(L<R&&nums[L]==nums[L+1])L++;
while(L<R&&nums[R]==nums[R-1])R--;
L++;
R--;
}
else if (sum < 0) L++;
else if (sum > 0) R--;
}
}
return list;
}
}
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
解题方案
思路
标签:排序和双指针
本题目因为要计算三个数,如果靠暴力枚举的话时间复杂度会到 O(n3)O(n^3)O(n3),需要降低时间复杂度
首先进行数组排序,时间复杂度 O(nlogn)O(nlogn)O(nlogn)
在数组 nums 中,进行遍历,每遍历一个值利用其下标i,形成一个固定值 nums[i]
再使用前指针指向 start = i + 1 处,后指针指向 end = nums.length - 1 处,也就是结尾处
根据 sum = nums[i] + nums[start] + nums[end] 的结果,判断 sum 与目标 target 的距离,如果更近则更新结果 ans
同时判断 sum 与 target 的大小关系,因为数组有序,如果 sum > target 则 end--,如果 sum < target 则 start++,如果 sum == target 则说明距离为 0 直接返回结果
整个遍历过程,固定值为 n 次,双指针为 n 次,时间复杂度为)O(n^2)
总时间复杂度:O(nlogn) + O(n^2) = O(n^2)
class Solution {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int ans = nums[0] + nums[1] + nums[2];
for(int i=0;i<nums.length;i++) {
int start = i+1, end = nums.length - 1;
while(start < end) {
int sum = nums[start] + nums[end] + nums[i];
if(Math.abs(target - sum) < Math.abs(target - ans))
ans = sum;
if(sum > target)
end--;
else if(sum < target)
start++;
else
return ans;
}
}
return ans;
}
}
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例:
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
在三数之和的基础上加一个循环。a遍历O(N)里嵌套b遍历O(N)再嵌套c,d双指针O(N)--> O(N^3)。 总比暴力法O(N^4)好些吧。
import java.util.ArrayList;
import java.util.Arrays;
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> list=new ArrayList();
Arrays.sort(nums);
if(nums.length<4)return list;
else{
for(int a=0;a<nums.length-3;a++){
if(a>=1&&nums[a]==nums[a-1])continue;
int length=nums.length;
for(int b=a+1;b<nums.length-2;b++){
if(b>=a+2&&nums[b]==nums[b-1])continue;
int c=b+1;
int d=length-1;
while(c<d){
int sum=nums[a]+nums[b]+nums[c]+nums[d];
if(sum<target)c++;
else if(sum>target)d--;
else{
list.add(Arrays.asList(nums[a],nums[b],nums[c],nums[d]));
while(c<d&&nums[c]==nums[c+1])c++;
while(c<d&&nums[d]==nums[d-1])d--;
c++;
d--;
}
}
}
}
}
return list;
}
}
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
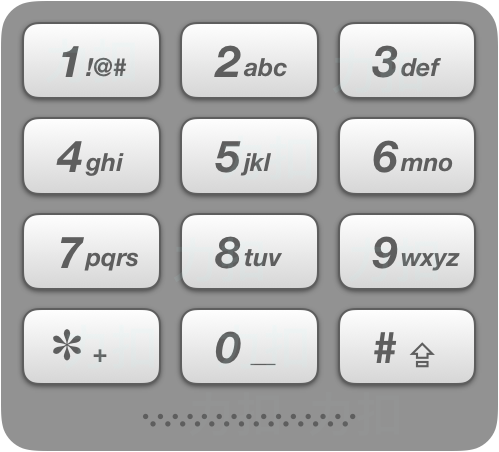
示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
import java.util.ArrayList;
class Solution {
Map<String,String> map=new HashMap<String,String>(){{
put("2","abc");
put("3","def");
put("4","ghi");
put("5","jkl");
put("6","mno");
put("7","pqrs");
put("8","tuv");
put("9","wxyz");
}};
String combination="";
public List<String> letterCombinations(String digits) {
if(digits.length()!=0)
back("",digits);
return list;
}
List<String> list=new ArrayList<>();
public void back(String combination,String digits){
if(digits.length()==0)
list.add(combination);
else{
String digist=digits.substring(0,1);
String letters=map.get(digist);
for(int i=0;i<letters.length();i++){
String letter=letters.substring(i,i+1);
back(combination+letter,digits.substring(1));
}
}
}
}
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
我们可以使用两个指针而不是一个指针。第一个指针从列表的开头向前移动 n+1n+1n+1 步,而第二个指针将从列表的开头出发。现在,这两个指针被 nnn 个结点分开。我们通过同时移动两个指针向前来保持这个恒定的间隔,直到第一个指针到达最后一个结点。此时第二个指针将指向从最后一个结点数起的第 nnn 个结点。我们重新链接第二个指针所引用的结点的 next 指针指向该结点的下下个结点
时间复杂度:O(L),该算法对含有 LLL 个结点的列表进行了一次遍历。因此时间复杂度为 O(L)。
空间复杂度:O(1),我们只用了常量级的额外空间。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int k) {
ListNode pre=new ListNode(0);
pre.next=head;
ListNode start=pre;ListNode end=pre;
while(k!=0){
start=start.next;
k--;
}
while(start.next!=null){
start=start.next;
end=end.next;
}
end.next=end.next.next;
return pre.next;
}
}
给定一个只包括 ‘(‘,‘)‘,‘{‘,‘}‘,‘[‘,‘]‘ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
输入: "()"
输出: true
示例 2:
输入: "()[]{}"
输出: true
import java.util.Stack;
class Solution {
public boolean isValid(String s) {
if(s.equals(""))return true;
Stack stack = new Stack();
stack.push(s.charAt(0));
for(int i=1;i<s.length();i++){
String str=stack.peek()+""+s.charAt(i);
if(str.equals("()")||str.equals("{}")|| str.equals("[]")){
stack.pop();
if(stack.isEmpty()&&i+1<s.length()){
stack.push(s.charAt(++i));
}
}else {
stack.push(s.charAt(i));
}
}
if(stack.isEmpty()) return true;
return false;
}
}
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:n = 3
输出:[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
我们以 n = 2 为例,画树形结构图。方法是 “做减法”。
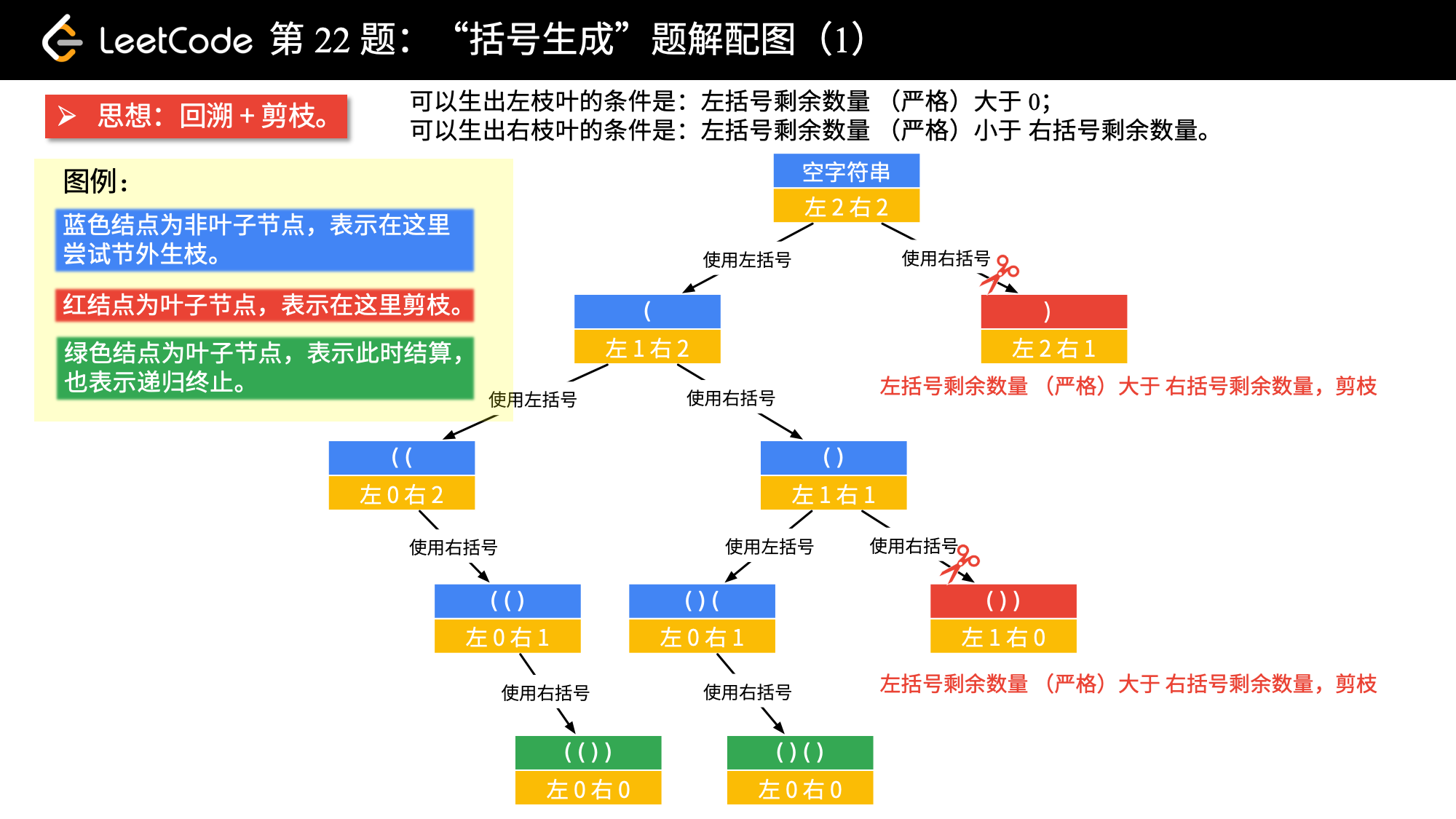
import java.util.ArrayList;
class Solution {
public List<String> generateParenthesis(int n) {
//深度优先遍历
List<String> list = new ArrayList();
if(n==0)return list;
generate("",n,n,list);
return list;
}
public void generate(String s,int left,int right,List<String> list){
//递归
if(left==0&&right==0){
list.add(s);
return;
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807
时间复杂度:O(max?(m,n)),假设 mmm 和 nnn 分别表示 l1l1l1 和 l2l2l2 的长度,上面的算法最多重复 max?(m,n) 次。
空间复杂度:O(max?(m,n)), 新列表的长度最多为 max?(m,n)+1。
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode newList=new ListNode(0);
ListNode List=newList;
//List=newList;
int m=0;
while(l1!=null||l2!=null){
if(l1==null){
l1=new ListNode(0);
}
if(l2==null){
l2=new ListNode(0);
}
newList.val=l1.val+l2.val+m;
m=0;
if(newList.val>=10){
m=1;
newList.val=newList.val-10;
}
if(l2.next!=null||l1.next!=null){
newList.next=new ListNode(0);
newList=newList.next;
}
l1=l1.next;
l2=l2.next;
}
if(m==1){
newList.next=new ListNode(1);
}
return List;
}
}
标签:除了 == 用两个 电话 owa div 返回 minus while
原文地址:https://www.cnblogs.com/lgh544/p/13064660.html