标签:分离 好的 操作 合并 ima std 时间 修改 位置
水了一堆cf的题以后又回来了
以前就了解过\(CDQ\)分治,但是一直没时间写。
前置知识:分治
分治的思想就是分而治之,即把一个大问题分解成多个小问题,再把小问题的答案合并到大问题,最终得到大问题的答案。
比如:在一个单调的数列\(a[1]...a[n]\)中查找某一个数\(x\)的位置。大问题即\(x\)是否在区间\([a[l],a[r]]\)中出现过。那么小问题就是\(x\)是否在\([a[l],mid]\)和\([mid+1,a[r]]\)中出现过。最后合并答案
又比如归并排序。每次有两个排序好的区间,每次合并两个区间,这也是分治的思想
要注意分治是一种思想而不是仅局限于二分。比如我要求\(n\leq10\)的问题,那我先求\(n\leq9\)的问题再把\(10\)的加上,这也算分治。
接下来是\(CDQ\)分治:
我们发现,某些分治的每个小问题之间是互不影响的。比如二分查找中区间\([l,mid]\)和区间\([mid+1,r]\)的情况互不影响,归并排序中区间\([l,mid]\)和区间\([mid+1,r]\)分别排序的情况也互不影响。
而另一些分治中小问题之间是有影响的。什么意思呢?举个例子:
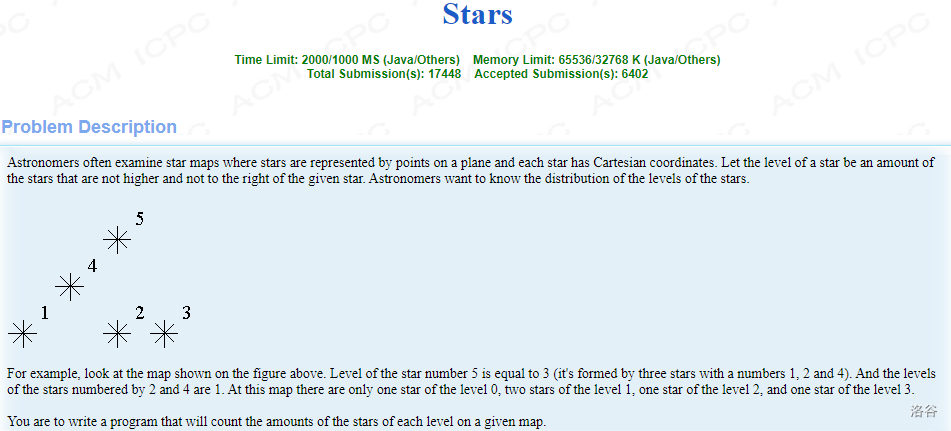
大体意思就是给你平面直角坐标的\(n\)个点,问你每个点左下方的点有多少。
比如图中的样例,我要求5号点左下方的点有哪些,如果用分治的思想求的话就必须要知道4号点的答案,这就是4号点对5号点的答案产生了影响。
这道题按照横坐标排序,然后对于纵坐标建立树状数组,每次查询修改就好了。
\(CDQ\)分治解决的就是小问题之间有影响的情况。
我们注意到在分治的过程中,与\(i\)无关的\([1,i-1]\)和\([i+1,n]\)会由于分割而慢慢地被分离开。对于\(j\)对\(i\)的贡献,我们在\(j\)与\(i\)被分开的时候去计算。.
我们要解决一系列问题,这些问题一般包含修改和查询操作,可以把这些问题排成一个序列,用一个区间\([L,R]\)表示。
分。递归处理左边区间\([L,M]\)和右边区间\([M+1,R]\)的问题。
治。合并两个子问题,同时考虑到\([L,M]\)内的修改对\([M+1,R]\)内的查询产生的影响。即,用左边的子问题帮助解决右边的子问题。
这个题如果图像化的话和上面那个题很像,只不过二维坐标系变成了三维坐标系。
我们没有必要按照他给定的顺序去处理。相应地,我们将这些元素以\(a,b,c\)为第一,二,三关键字排序,这样排好序后的元素,对于\(i<j\),一定有\(a_i<a_j\),这样我们就处理掉了一维,剩下的问题就变成了\(\forall j<i,b_j<b_i且c_j<c_i\)的\(j\)有多少个。
考虑现在处理的区间是\([l,r]\),我们将他分成区间\([l,mid]\)和\([mid+1,r]\)。
然后我们对两个区间按照第二关键字\(b\)排序。这样虽然每个区间里\(a\)的顺序被打乱了,但是左边区间\(a\)的值仍然比右边区间小,也就是说如果我们单纯考虑左边对于右边的贡献是可以的。
对于每个右边区间的元素\(i\),统计左边区间对于它的贡献。开始遍历左边区间的元素\(j\),如果\(b_j<=b_i\),也就是说\(j\)有可能对\(i\)产生贡献,这时候把\(c_j\)加到树状数组里面;当\(b_j>b_i\)时,说明以后的\(j\)也不会对当前的\(i\)产生影响了,这时候树状数组查询\(c\leq c_i\)的数的个数并累加到答案里面。然后把 \(i++\),换下一个继续统计。
大体思路就是这样,但是有些细节问题需要注意,比如关键字的处理和树状数组的清空(因为每次使用树状数组只对特定的两个区间有效),代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 200005;
struct node
{
int a, b, c, cnt, ans;
}a[N], b[N];
int sum[N << 2], n, k, ans[N], cn;
int lowbit(int x){return x & (-x);}
void add(int x, int t){for(;x <= k; x += lowbit(x)) sum[x] += t;}
int query(int x){int ans = 0;for(; x; x -= lowbit(x)) ans += sum[x];return ans;}
bool cmp1(node a, node b)
{
if(a.a != b.a) return a.a < b.a;
if(a.b != b.b) return a.b < b.b;
return a.c < b.c;
}
bool cmp2(node a, node b)
{
if(a.b != b.b) return a.b < b.b;
if(a.c != b.c) return a.c < b.c;
return a.a < b.a;
}
void cdq(int l, int r)
{
if(l == r) return;
int mid = l + r >> 1;
cdq(l, mid); cdq(mid + 1, r);
sort(a + l, a + mid + 1, cmp2);
sort(a + mid + 1, a + r + 1, cmp2);
int i = mid + 1, j = l;
for(; i <= r; i ++)
{
while(a[j].b <= a[i].b && j <= mid) add(a[j].c, a[j].cnt), j ++;
a[i].ans += query(a[i].c);
}
for(i = l; i < j; i ++) add(a[i].c, -a[i].cnt);
}
int main()
{
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; i ++) scanf("%d%d%d", &b[i].a, &b[i].b, &b[i].c);
sort(b + 1, b + 1 + n, cmp1);
int ct = 0;
for(int i = 1; i <= n; i ++)
{
ct ++;
if(b[i].a != b[i + 1].a || b[i].b != b[i + 1].b || b[i].c != b[i + 1].c) a[++cn] = b[i], a[cn].cnt = ct, ct = 0;
}
cdq(1, cn);
for(int i = 1; i <= cn; i ++) ans[a[i].ans + a[i].cnt - 1] += a[i].cnt;
for(int i = 0; i < n; i ++) printf("%d\n", ans[i]);
}
标签:分离 好的 操作 合并 ima std 时间 修改 位置
原文地址:https://www.cnblogs.com/lcezych/p/13095828.html