标签:作用 net div 距离 计算 评价 超过 变量 core
熵值法的主要目的是对指标体系进行赋权
熵越大说明系统越混乱,携带的信息越少,权重越小;熵越小说明系统越有序,携带的信息越多,权重越大。
熵值法是一种客观赋权方法,,借鉴了信息熵思想,它通过计算指标的信息熵,根据指标的相对变化程度对系统整体的影响来决定指标的权重,即根据各个指标标志值的差异程度来进行赋权,从而得出各个指标相应的权重,相对变化程度大的指标具有较大的权重。
假设有m个待评价样本,n项评价指标,形成原始指标数据矩阵:
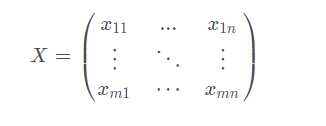
其中Xij表示第 i 个样本第 j 项评价指标的数值。
对于某项指标Xj,样本的离散程度越大,则该指标在综合评价中所起的作用就越大。如果该指标的标志值全部相等,则表示该指标在综合评价中不起作用。
为消除因量纲不同对评价结果的影响,需要对各指标进行标准化处理。
若所用指标的值越大越好(正向指标:)
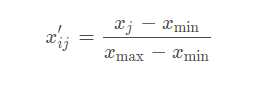
若所用指标的值越小越好(负向指标:)
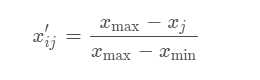
其中xj为第j项指标值, xmax为第j项指标的最大值, xmin为第j项指标的最小值。或者:
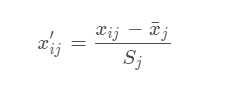
计算第 j 个指标中,第 i 个样本标志值的权重:
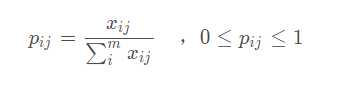
因此,可以建立数据的比重矩阵
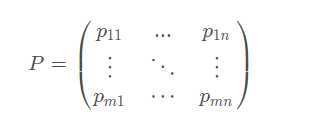
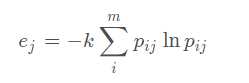
其中,常数
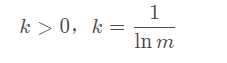
保证0<=ej<=1,即最大为1
所以,第j个指标的熵值为
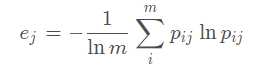
熵值法根据各个指标标志值的差异程度来进行赋权,从而得出各个指标相应的权重
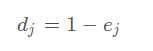
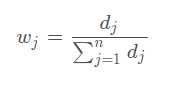
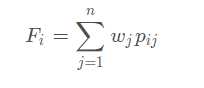
原理讲解引自:https://blog.csdn.net/qq_42374697/article/details/105901229
评价下表中20条河流的水质情况。(熵权法和优劣解距离法对比)
注:含氧量越高越好;PH值越接近7越好;细菌总数越少越好;植物性营养物量介于10‐20之间最佳,超过20或低于10均不好。
|
河流 |
含氧量(ppm) |
PH值 |
细菌总数(个/mL) |
植物性营养物量(ppm) |
|
A |
4.69 |
6.59 |
51 |
11.94 |
|
B |
2.03 |
7.86 |
19 |
6.46 |
|
C |
9.11 |
6.31 |
46 |
8.91 |
|
D |
8.61 |
7.05 |
46 |
26.43 |
|
E |
7.13 |
6.5 |
50 |
23.57 |
|
F |
2.39 |
6.77 |
38 |
24.62 |
|
G |
7.69 |
6.79 |
38 |
6.01 |
|
H |
9.3 |
6.81 |
27 |
31.57 |
|
I |
5.45 |
7.62 |
5 |
18.46 |
|
J |
6.19 |
7.27 |
17 |
7.51 |
|
K |
7.93 |
7.53 |
9 |
6.52 |
|
L |
4.4 |
7.28 |
17 |
25.3 |
|
M |
7.46 |
8.24 |
23 |
14.42 |
|
N |
2.01 |
5.55 |
47 |
26.31 |
|
O |
2.04 |
6.4 |
23 |
17.91 |
|
P |
7.73 |
6.14 |
52 |
15.72 |
|
Q |
6.35 |
7.58 |
25 |
29.46 |
|
R |
8.29 |
8.41 |
39 |
12.02 |
|
S |
3.54 |
7.27 |
54 |
3.16 |
|
T |
7.44 |
6.26 |
8 |
28.41 |
.mat数据:在MATLAB里面随便创建一个变量,将表格中的数据粘贴进变量中,再另存为.mat数据就行。
main.m
%% 数据读取
clear,clc
load rivers_data.mat
%% 正向化处理
[n,m] = size(datas_matrix);
% 正向化处理的数据所在列
Pos = [2,3,4];
% 指标类型:1:极小型,2:中间型,3:区间型
ch = [2,1,3];
% 循环处理每一列
for i = 1 : size(Pos,2)
datas_matrix(:,Pos(i)) = Forward_processing(datas_matrix(:,Pos(i)),ch(i),Pos(i));
end
%% 矩阵标准化
datas_S_matrix = datas_matrix ./ repmat(sum(datas_matrix.*datas_matrix) .^ 0.5, n, 1);
%%
model = ["A","B","C","D","E","F","G","H","I","J","K","L","M","N","O","P","Q","R","S","T"];
%% 熵权法
p = datas_S_matrix./sum(datas_S_matrix);
k = 1/log(n);
r = zeros(n,m);
for i = 1:n
for j = 1:m
if p(i,j) == 0
r(i,j) = 0;
else
r(i,j) = log(p(i,j));
end
end
end
e = -k*sum(p.*r,1);
d = ones(1,m)-e;
weight = d./sum(d);
score = sum(weight.*datas_S_matrix,2);
results1 = 0 + (100-0)/(max(score)-min(score)).*(score - min(score));
[sorted_score,index] = sort(results1 ,‘descend‘);
rivers1 = [];
for i = 1:n
rivers1 = [rivers1;model(index(i))];
end
s = [rivers1,sorted_score];
%% 绘图
bar(sorted_score);
title(‘熵权法‘)
set(gca,‘XTick‘,1:20)
set(gca, ‘xticklabel‘,{rivers1{1:20}});
%% 保存到文件
xlswrite(‘output.xls‘,s,‘Sheet1‘);
Forward_processing.m
function [posit_x] = Forward_processing(x,type,~)
if type == 1 %极小型
%正向化
posit_x = max(x) - x;
elseif type == 2 %中间型
best = 7;
M = max(abs(x-best));
posit_x = 1 - abs(x-best) / M;
elseif type == 3 %区间型
a = 10;
b = 20;
r_x = size(x,1);
M = max([a-min(x),max(x)-b]);
posit_x = zeros(r_x,1);
for i = 1: r_x
if x(i) < a
posit_x(i) = 1-(a-x(i))/M;
elseif x(i) > b
posit_x(i) = 1-(x(i)-b)/M;
else
posit_x(i) = 1;
end
end
end
end
标签:作用 net div 距离 计算 评价 超过 变量 core
原文地址:https://www.cnblogs.com/Mayfly-nymph/p/13096812.html