标签:lcs 存储 最长重复子串 png -- ges mat 不用 das
## 最长公共子序列 Longest common subsquence # s1 = "a b d a c e" # s2 = "b a b c e" # LCS = ["abce", "abce"] # 长度4 ## 1 brute force ## 递归解法 从单个字符解决问题 某位置处若两字符相等,则同时序号增加,最长长度+1 ## 若不相等,则需要s1增加1个位置,或者s2增加一个位置,哪个大返回哪个。 def lcs_brute_force(s1, s2): def lcs_recursion(i, j): if i >= len(s1) or j >= len(s2): return 0 elif s1[i] == s2[j]: return 1 + lcs_recursion(i + 1, j + 1) else: return max(lcs_recursion(i + 1, j), lcs_recursion(i, j + 1)) return lcs_recursion(0, 0) s1 = "abdace" s2 = "babce" print(lcs_brute_force(s1, s2)) ## 递归算法的时间复杂度是指数级的,因为会重复计算,重复递归。解决办法是借助一个二位数组,记录已经算出来的lcs, ## 下次根据i和j直接去表里查。这样下来时间复杂度和空间复杂度都是O(m*n) ## 递归算法是bottum自底向上回溯

##########动态规划################# # 思路是利用一个二位数组(矩阵),正向计算,不用递归到底再回溯, # 它每次都把算出来的值记录再矩阵里,计算下一个的时候直接查表 # 先初始化一个二位数组用来存储每一步计算出的lcs def init_matrix(s1, s2): matrix = [] for i in range(len(s1)+1): matrix.append([0] * (len(s2)+1)) return matrix s1 = "bd" s2 = "abcd" def lcs_dp(s1, s2): matrix = init_matrix(s1, s2) for i in range(1, len(s1)+1): for j in range(1, len(s2)+1): if s1[i-1] == s2[j-1]: matrix[i][j] = 1 + matrix[i-1][j-1] else: matrix[i][j] = max(matrix[i-1][j], matrix[i][j-1]) return matrix[i][j] print(lcs_dp(s1, s2))
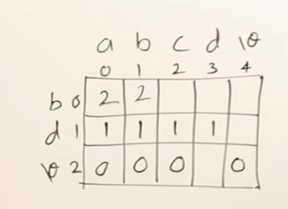

寻找子序列内容,从矩阵最后一个元素往回回溯就行。
——————————————————————————————————————————————————
标签:lcs 存储 最长重复子串 png -- ges mat 不用 das
原文地址:https://www.cnblogs.com/importsober/p/13113483.html