标签:bool distrib style typedef visit 递增 编程 eva das
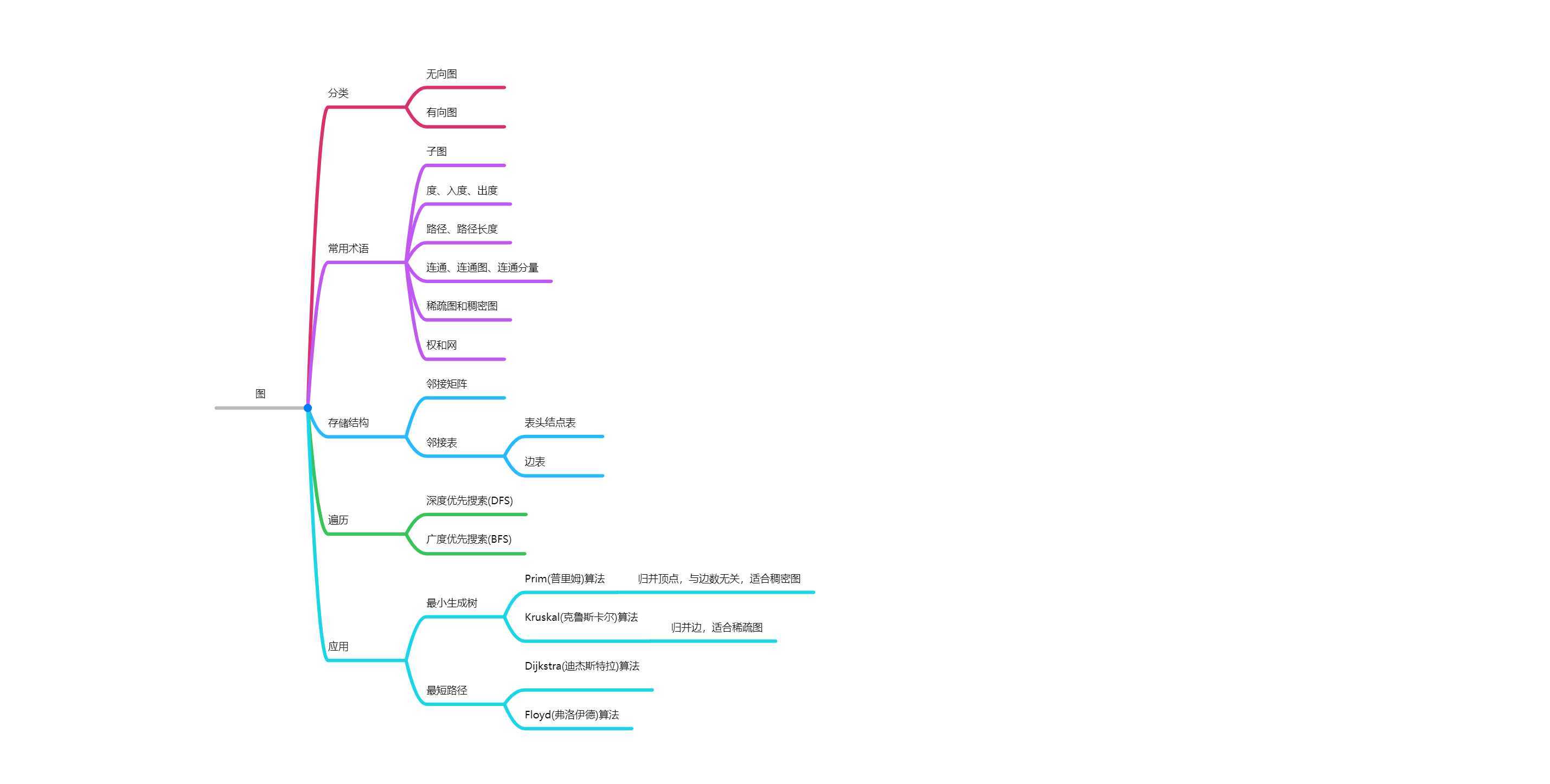
第六章学习的主要内容如下:
这是课后习题的一道题:
1 void DFS_AM(AMGraph G, int v) 2 { //图G为邻接矩阵类型 3 cout << v << " "; //访问第v个顶点 4 visited[v] = true; 5 for(w=G.vexnum-1; w>=0; --w) //依次检查邻接矩阵v所在的行 6 if((G.arcs[v][w]!=0)&& (!visited[w])) 7 DFS_AM(G, w); 8 } 9 void DFSTraverse(Graph G) 10 { // 对图 G 作深度优先遍历 11 for(v=0; v<G.vexnum; ++v) visited[v] = FALSE; 12 for (v=0; v<G.vexnum; v++) 13 if (!visited[v]) DFS(G, v); //对尚未访问的顶点调用DFS 14 }
输出结果: 0 1 7 6 5 4 2 3
第一眼看可能觉得这个代码没什么特别的地方,仔细看一遍会发现他是从每行的右边向左边遍历的,所以在看代码的时候一定要仔细,防止有坑。
我一直有些不太理解生成树、最小生成树,尤其是做这周作业的时候,更加懵了。我就再去看了一遍书和老师的视频后,但是还是不懂,我就去查了一下博客,这篇博客讲的很清楚,而且还有详细地讲Prim、Kruskal算法,跟我有一样问题的同学可以去看看https://blog.csdn.net/weixin_42562514/article/details/85234342
这周有两道编程题,第一道:
7-1 列出连通集 (30分) 给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。 输入格式: 输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。 输出格式: 按照"{ v1 v2... vk}"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
这道题不算特别难,只要知道该把括号放在哪个循环里,打出代码应该没什么问题
这是我的代码
#include <iostream> #include <queue> #include <cstring> using namespace std; typedef struct { int arcs[10][10]; int vexnum,arcnum; }AMGraph; void CreateUDN(AMGraph &G) { cin >> G.vexnum >> G.arcnum; int i,j,v1,v2; for(i=0;i<G.vexnum;i++) { for(j=0;j<G.vexnum;j++) { G.arcs[i][j] = 0; } } for(i=0;i<G.arcnum;i++) { cin >> v1 >> v2; G.arcs[v1][v2] = G.arcs[v2][v1] = 1; } } bool visited[10] = {false}; void DFS_AM(AMGraph G,int v) { int w; cout << v <<" "; visited[v]=true; for(w=0;w<G.vexnum;w++) { if((G.arcs[v][w]!=0)&&(!visited[w])) { DFS_AM(G,w); } } } void BFS_AM(AMGraph G, int v) { visited[v] = 1; queue<int> q; q.push(v); while(q.size() != 0){ int m = q.front(); q.pop(); cout << m << " "; for(int i=0; i<G.vexnum; i++) { if(G.arcs[i][m] == 1 && visited[i] == 0) { visited[i] = 1; q.push(i); } } } } int main() { AMGraph g; CreateUDN(g); for(int i=0; i<g.vexnum; i++){ if(visited[i] == 0) { cout << "{ "; DFS_AM(g,i); cout << "}" << endl; } } memset(visited, false, 10); //将visited数组全部重置为false for(int i=0; i<g.vexnum; i++) { if(visited[i] == 0) //每个连通集输出 { cout << "{ "; BFS_AM(g,i); cout << "}" << endl; } } return 0; }
memset(visited, false, 10)这是一个cstring库里的函数,可以把visited数组里的10个元素置为false,挺方便的,建议大家使用。
第二题:
7-1 拯救007 (30分) 在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。) 设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。 输入格式: 首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D。随后 N 行,每行给出一条鳄鱼的 (x,y) 坐标。注意:不会有两条鳄鱼待在同一个点上。 输出格式: 如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。
这道题就比较难理解,我光看题目有点理解不了,所以自己画了一个图,对着图来理解这道题目会好理解很多。这道题一定要记得单独讨论一步可以上岸的情况,我开始没有注意到这点,是去看了一下别人的代码之后想到的,大家如果还是无法理解这道题,可以去看看这篇博客https://blog.csdn.net/weixin_43581819/article/details/104937471?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase,他的方法会好理解很多
我的代码如下:
#include <iostream> #include <cmath> using namespace std; double d; //一次能跳的最大距离 int n,flag = 0; int visited[101][101]; //标记数组 int x[101],y[101]; //鳄鱼的x、y下标 void dfs(int a, int b) //广度优先遍历 { if(a+d>=100||b+d>=100||a-d<=0||b-d<=0) //成功跳出 { flag = 1; return; } visited[a][b] = 1; //将此坐标设为已经访问过 for(int i=0; i<n; i++) { double k,h; k = a - x[i]; h = b - y[i]; if((k*k + h*h <= d*d)&&!visited[x[i]][y[i]]) //该点可以跳到且未被访问 { dfs(x[i], y[i]); } } visited[a][b] = 0; return; } int main() { cin >> n >> d; for(int i=0; i<n; i++) //输入鳄鱼坐标 { double h, k; cin >> h >> k; x[i] = h + 50; y[i] = k + 50; } if(d>=42.5) //一次就可以跳出来 { cout << "Yes" <<endl; return 0; } for(int i=0;i<n;i++) { if(sqrt((x[i]-50)*(x[i]-50)+(y[i]-50)*(y[i]-50))<=d+7.5) { dfs(x[i], y[i]); } } if(flag) cout << "Yes" <<endl; if(!flag) cout << "No" <<endl; return 0; }
这两周学习明显感觉内容有点越来越难了,希望自己上课的时候可以高效一点,下课可以自觉地去复现老师讲的和书上的代码!
标签:bool distrib style typedef visit 递增 编程 eva das
原文地址:https://www.cnblogs.com/xuzhihan/p/13118189.html