标签:初始 一段 模型 没有 智能 nim 需要 应该 作用
问题回顾:
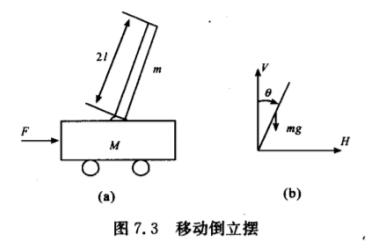
??例7.22考虑图7.3所示的移动倒立摆。设M=2kg,m=0.1kg,l=0.5m。设计带降维观测器的状态反馈系统使得倒立摆在垂直位置。
建立模型
??易得,该系统状态空间模型为:
\[ \begin{bmatrix}
\dot x_1 \ \dot x_3 \ \dot x_2 \ \dot x_4
\end{bmatrix}
=
\begin{bmatrix}
0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ \frac{3(M+m)g}{(4M+m)l} & 0 & 0 & 0 \ -\frac{3mg}{4M+m} & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
x_1 \ x_3 \ x_2 \ x_4
\end{bmatrix}
+
\begin{bmatrix}
0 \ 0 \ - \frac{3}{(4M+m)l} \ \frac{4}{4M+m}
\end{bmatrix}
F \y =
\begin{bmatrix}
1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
x_1 \ x_3 \ x_2 \ x_4
\end{bmatrix}
\]
??其中,\(x1= θ\) 是摆杆与垂直位置的夹角;\(x3\) 是小车的位移;\(x2=\dot θ\)表示摆杆的角速率,\(x4\) 表示小车的平移速度;\(F\) 是控制输入。
??代入M、m和l的值可得系统状态空间模型
\[ \begin{aligned}
&\dot x=Ax+Bu \ &y =Cx
\end{aligned}
\]
??其中
\[A =
\begin{bmatrix}
0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ 15.244 & 0 & 0 & 0 \ -0.363 & 0 & 0& 0
\end{bmatrix}
B =
\begin{bmatrix}
0 \ 0 \ -0.741 \ 0.494
\end{bmatrix}
C =
\begin{bmatrix}
1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0
\end{bmatrix}
\]
计算反馈增益矩阵K
??为了使系统具有较短的调节时间(取 \(t_s ≈ 2s\) )和适当的阻尼比(取 \(ξ=0.5\) ),期望闭环极点可取为
\[λ_{1,2} = -2 ± j 2\sqrt{3} \quad λ_3= λ_4 = - 10
\]
??由书中算法2编写matlab 程序
K_ba = [1600,720,211.244,24];
M = [0,-20.6,0,1; -20.6,0,1,0;0,1,0,0;1,0,0,0];
Qc = [B,A*B,A*A*B,A*A*A*B];
P = Qc*M;
K = K_ba *P^-1
??计算得
\[K =
\begin{bmatrix}
-535.8453 & -110.2916 & -376.1486& -116.8543
\end{bmatrix}
\]
计算降维观测器反馈增益矩阵H
??由状态空间模型可以看出,需要进行观测的状态量为摆杆的角速率 \(x2\) 以及小车的平移速度 \(x4\) 。
??取降维观测器期望极点:
\[λ_{1,2} ^*= a ± j b
\]
??设
\[H =
\begin{bmatrix}
h_{11} & h_{12} \ h_{21} &h_{22}
\end{bmatrix}
\]
??由
\[|sI - (A_{22} - HA_{12})| = [s - (a + jb)][s - (a - jb)]
\]
??由于上述式子得到的方程组未知量个数多于方程个数,因此 取 \(h_{11} = -a、h_{12} = 1\),算得
\[H =
\begin{bmatrix}
-a & 1 \ -b^2 & -a
\end{bmatrix}
\]
??得降维观测器状态空间模型:
\[\begin{aligned}
& \dot z = (A_{22}-HA_{12})\hat x + (B_2 - HB_1)u + (A_{21} - HA_{11})y \ & \hat x_2 = z + Hy
\end{aligned}
\]
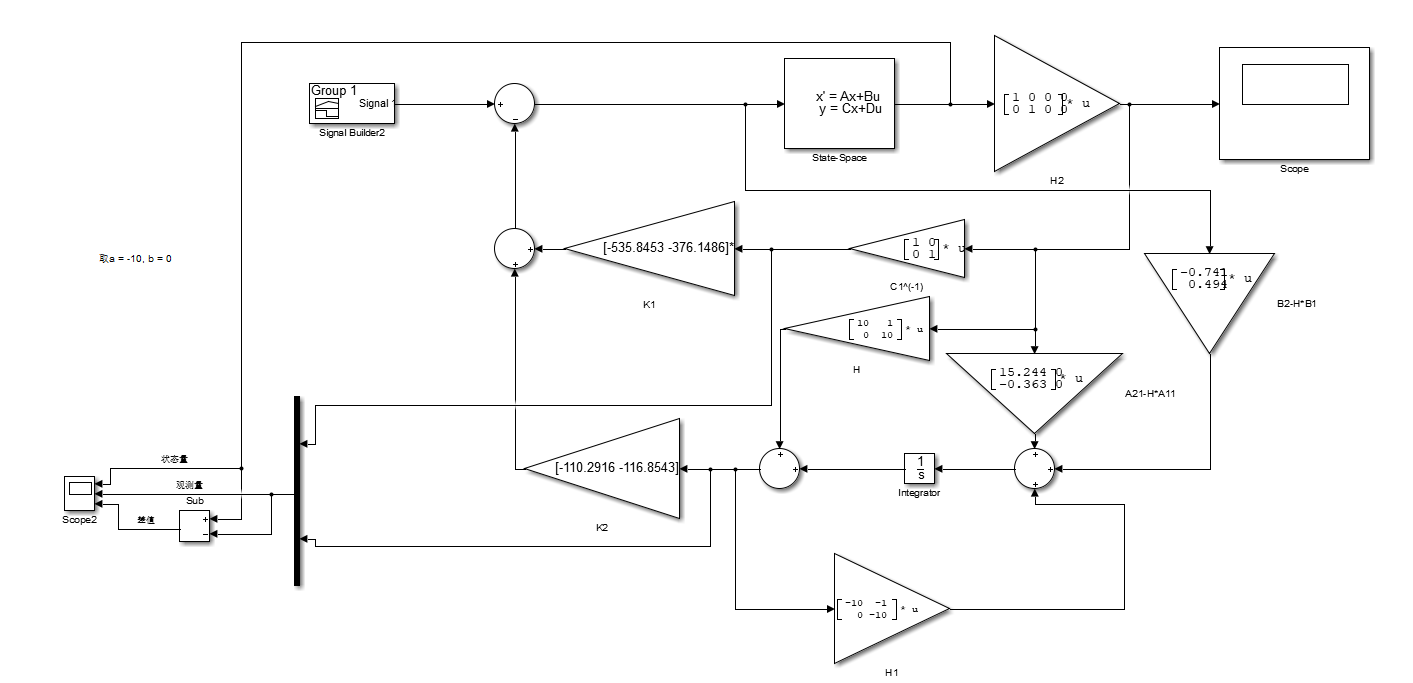
搭建Simulink模型
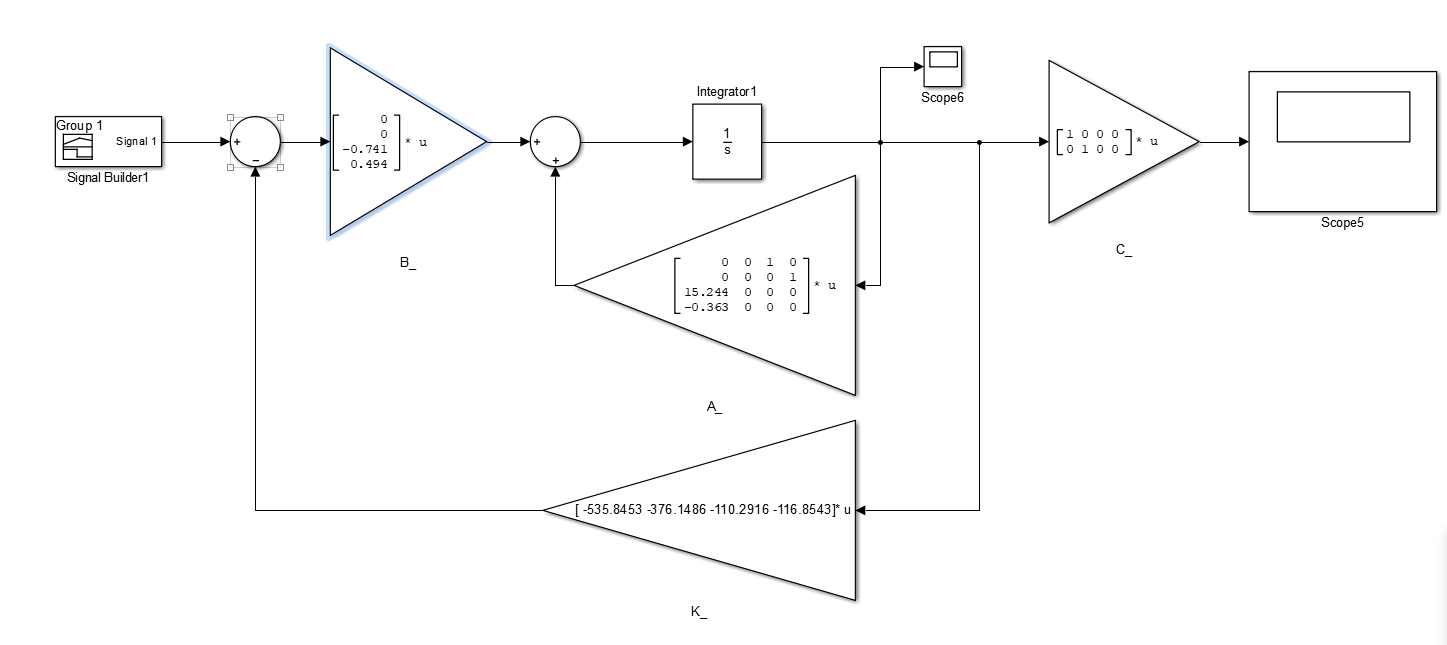
??搭建模型如下:
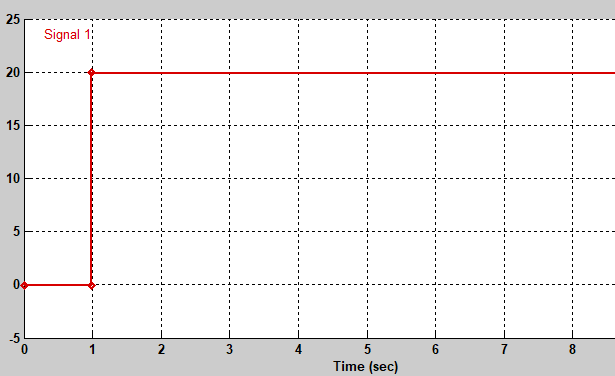
??输入阶跃信号:
??输出结果:
??由结果可知,该状态反馈能够使得倒立摆在2s内进入稳定区,故K满足要求。
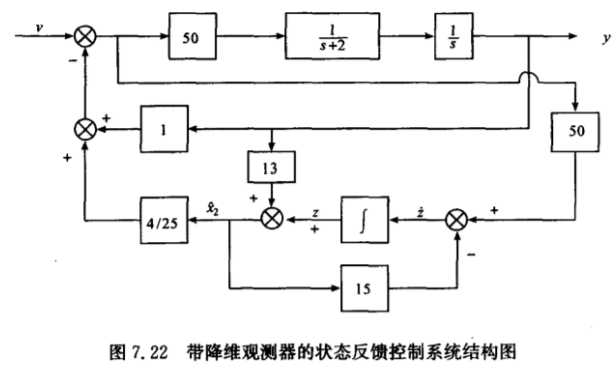
??参照书P406页图7.22
??在Simulink中搭建带降维观测器的状态反馈控制系统结构:
??同样输入阶跃信号:
- 验证降维状态器
??取降维观测器期望极点为
\[λ_{1,2} ^*= -10
\]
??则其反馈增益矩阵H为:
\[H =
\begin{bmatrix}
10 & 1 \ 0 & 10
\end{bmatrix}
\]
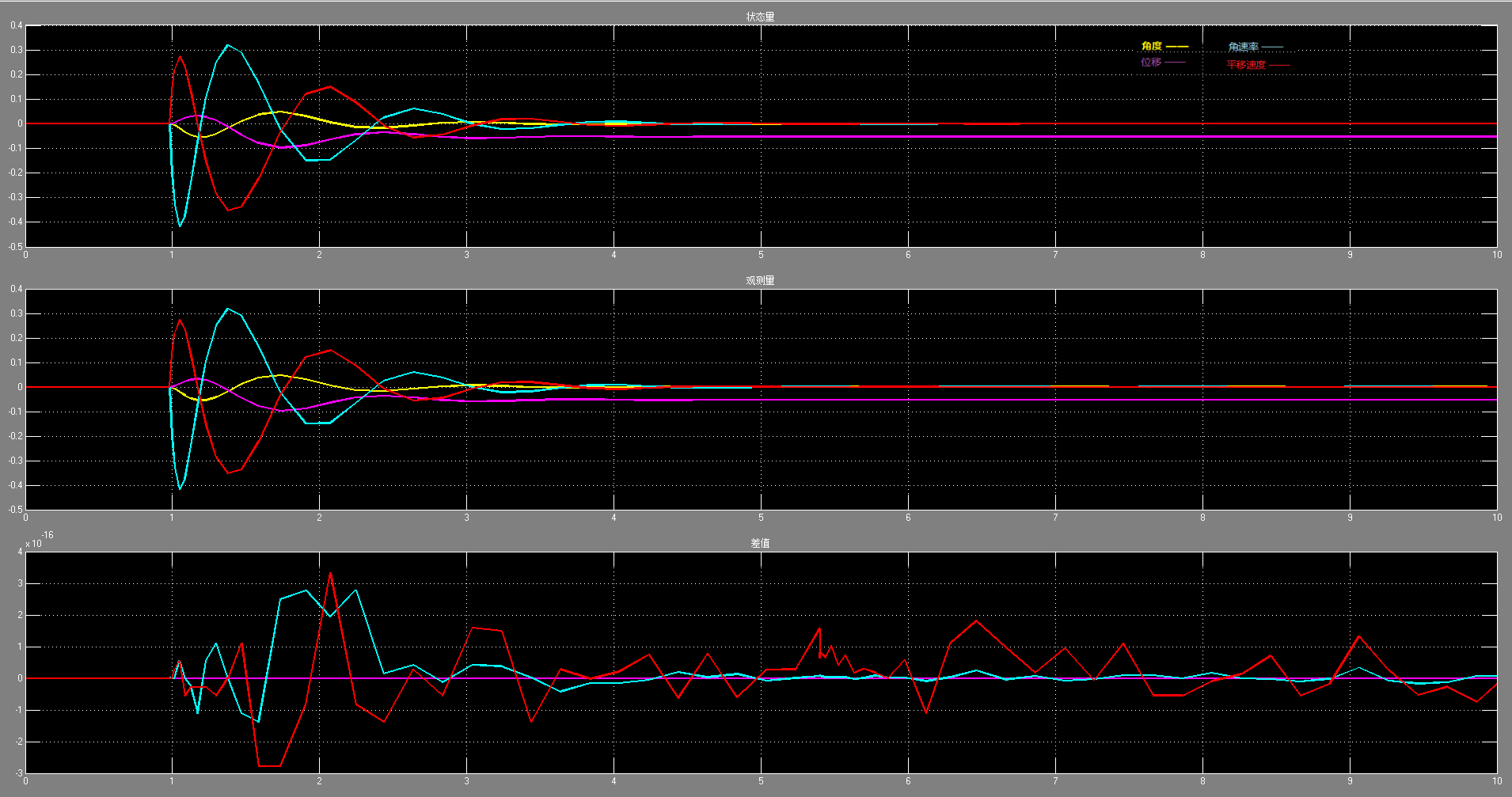
??观察结果如下图,从上至下依次为系统状态量 \(x\),观测量 \(\hat x\),以及两者之间的差值:
??由差值曲线可以看出,观测值与实际值之间的差值精度已经达到了 \(1 * 10^{-16}\),因此H的选择是符合要求的。
??输出结果如下图所示:
??由上图可以看出,在 \(t = 1s\)施加 \(F = 20N\) 的力之后,小车通过运动使得倒立摆在 2s 之后能够稳定在垂直状态,说明利用降维观测器的状态反馈控制起到了效果。
??这里主要谈及整个控制过程中我理解的小车的实际运动状况。
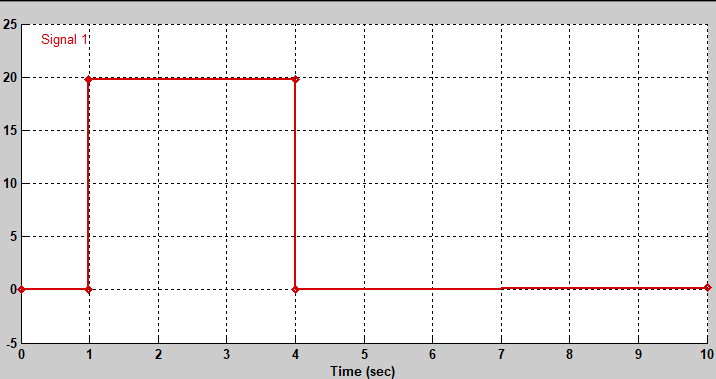
??不妨引入一个时间宽度为 3 s 的脉冲输入信号,如下图所示:
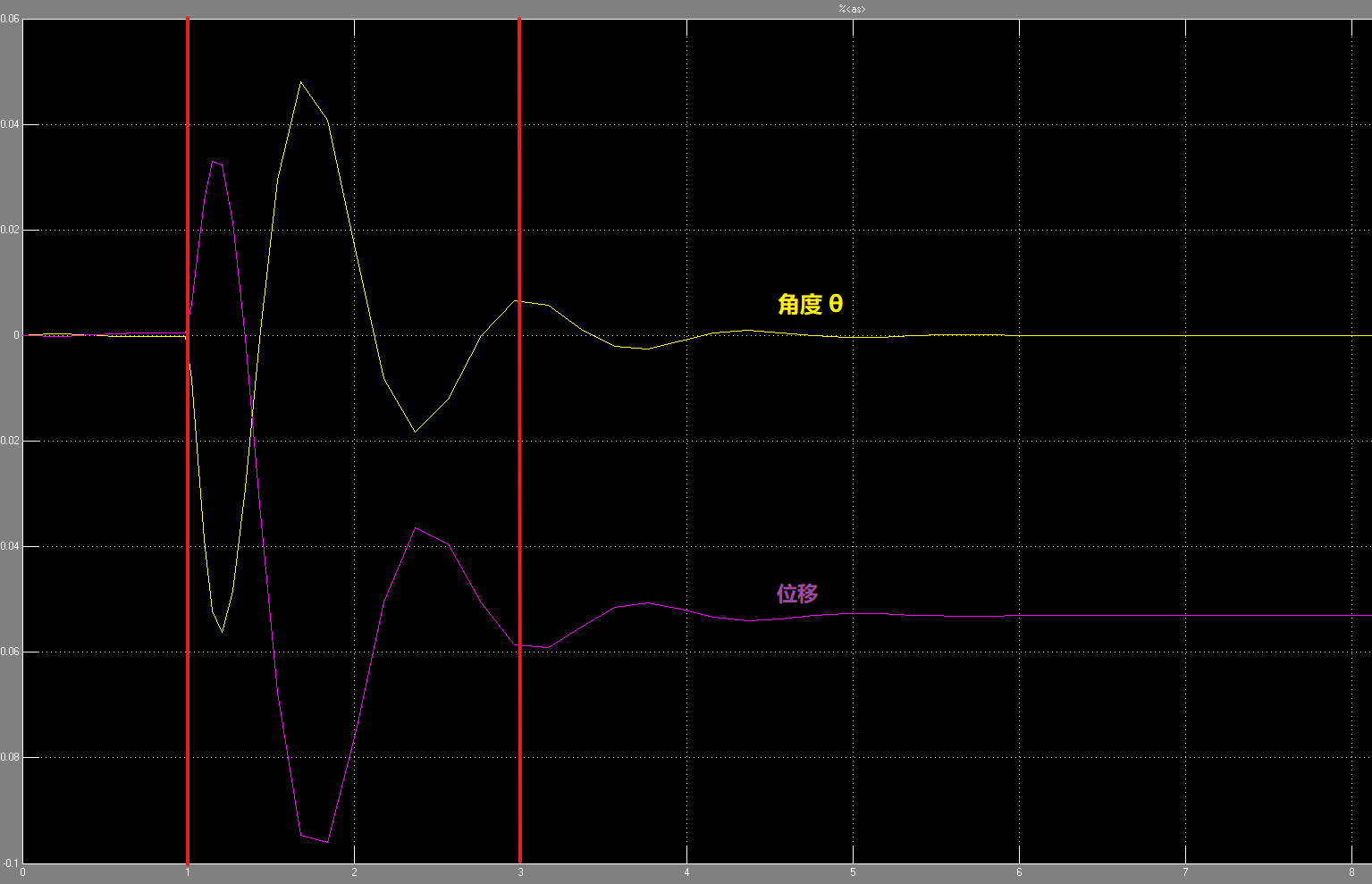
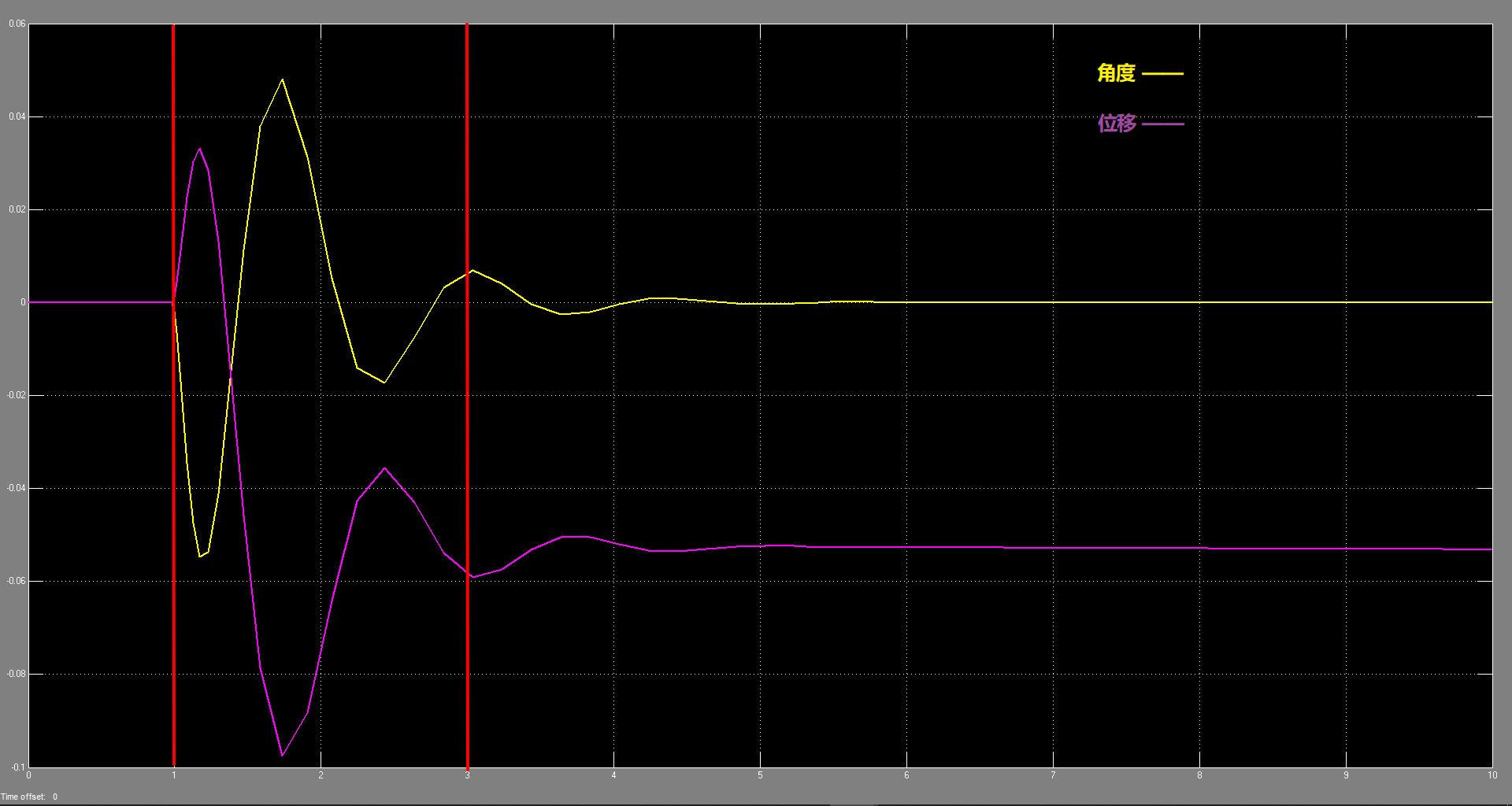
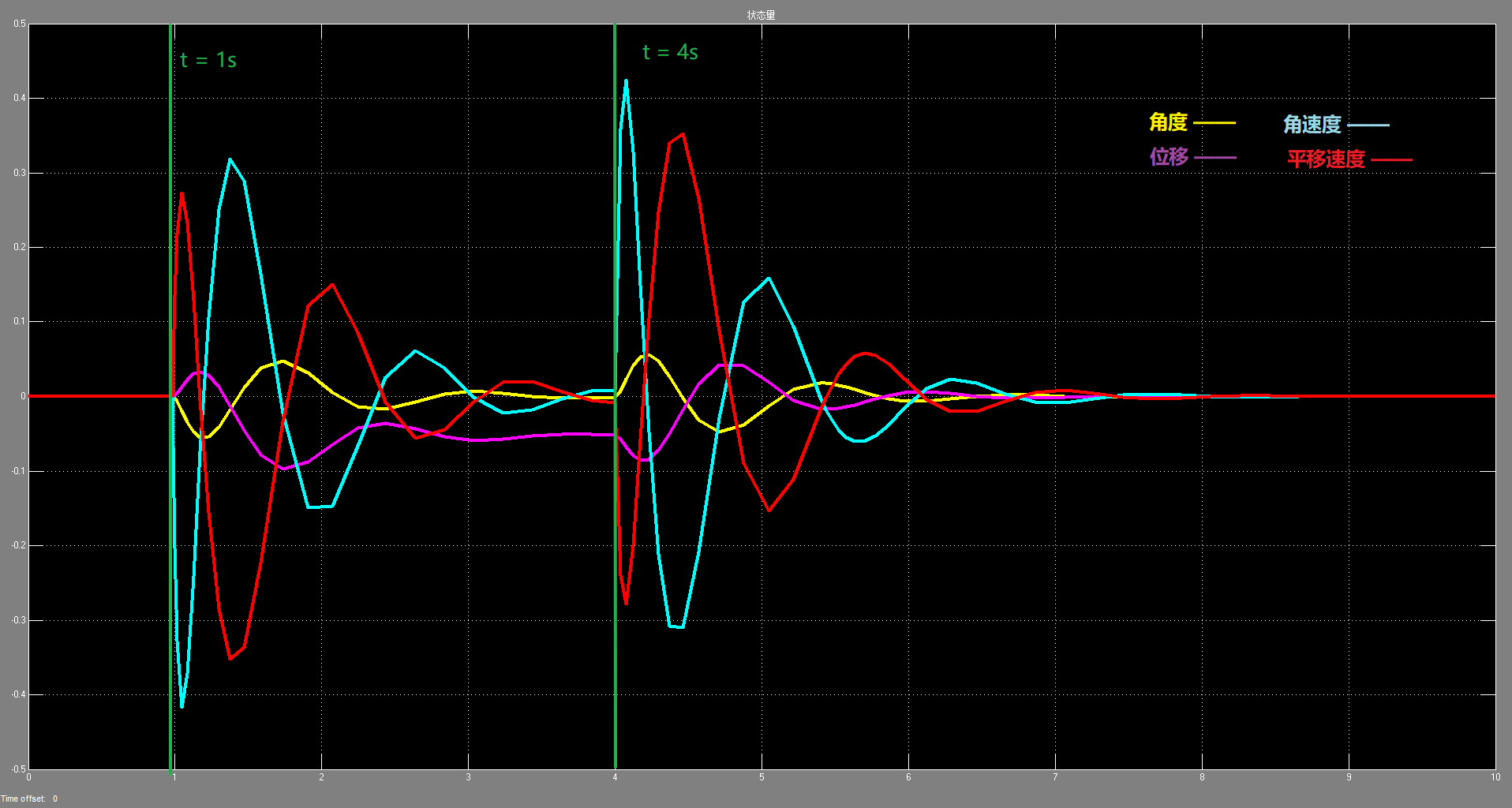
??此时观察系统状态如下图所示:
??从图中曲线可以看出:
- 当在 t = 1s 时,对小车施加一个 F = 20N 的向前的力之后:
- 在 \(t ∈ [1, 4]\) 时间段内:
??小车先是向前移动了一小段距离(紫色曲线),此时平移速度(红色曲线)先是增加,随后受控制器作用立刻以一个较大的反向加速度向后运动,在这个过程中倒立摆角度(黄色曲线)先是在小车前进的时候向后倒,随后在小车后退的时候往前倒。经过这样的2次振荡运动之后小车最终静止在 位移 ≈ -0.05 处,其余状态量(包括倒立摆角度及角速度、小车平移速度)趋于0.
??在这个地方,前面的实验是用的阶跃信号,因此我一直没有想明白为什么位移会稳定在一个固定的值,而不是像我之前参加智能车竞赛过程中直立小车会因为为了保持前进过程中的平衡状态而不断往前运动(正反馈)。不过在引入脉冲信号之后我想明白了:
- 当在 t = 4s 时,对小车施加向前的力撤消之后:
- 在 \(t ∈ [4,6]\) 时间段内:
??小车以与上述运动过程相反的动作状态进行运动,最终回到原点(位移 = 0),其余状态量趋于0。
??为什么会有上面的运动过程呢?我的理解是,当施加一个外力之后,在短暂的时间内,电机受控制系统控制产生的力矩低于外力,因此会先往前行进一段距离,在控制器控制力度增大后,电力力矩大于外力,小车开始后退,并使得倒立摆从向后倾覆的状态变为向前倾覆,因此小车又需要往前运动以保证倒立摆保持垂直状态,经过几次调整之后,倒立摆静止在垂直位置,但是此时外力F仍作用在小车上,也就是说,小车电机产生的平衡外力的力矩依然存在,所以小车此时的位移应该是一个不趋于0的值;当外力撤消之后,小车不再需要额外的电机力矩平衡外力,因此会往回运动,并最终保持在初始状态,此时所有状态量(包括位移、角度、角速度、平移速度)均趋于0。
基于降维观测器的状态反馈小车倒立摆控制系统Simulink建模
标签:初始 一段 模型 没有 智能 nim 需要 应该 作用
原文地址:https://www.cnblogs.com/beta-1999/p/13121569.html