标签:lis arc 网络 cab list mvn 为什么 访问 play
思维导图
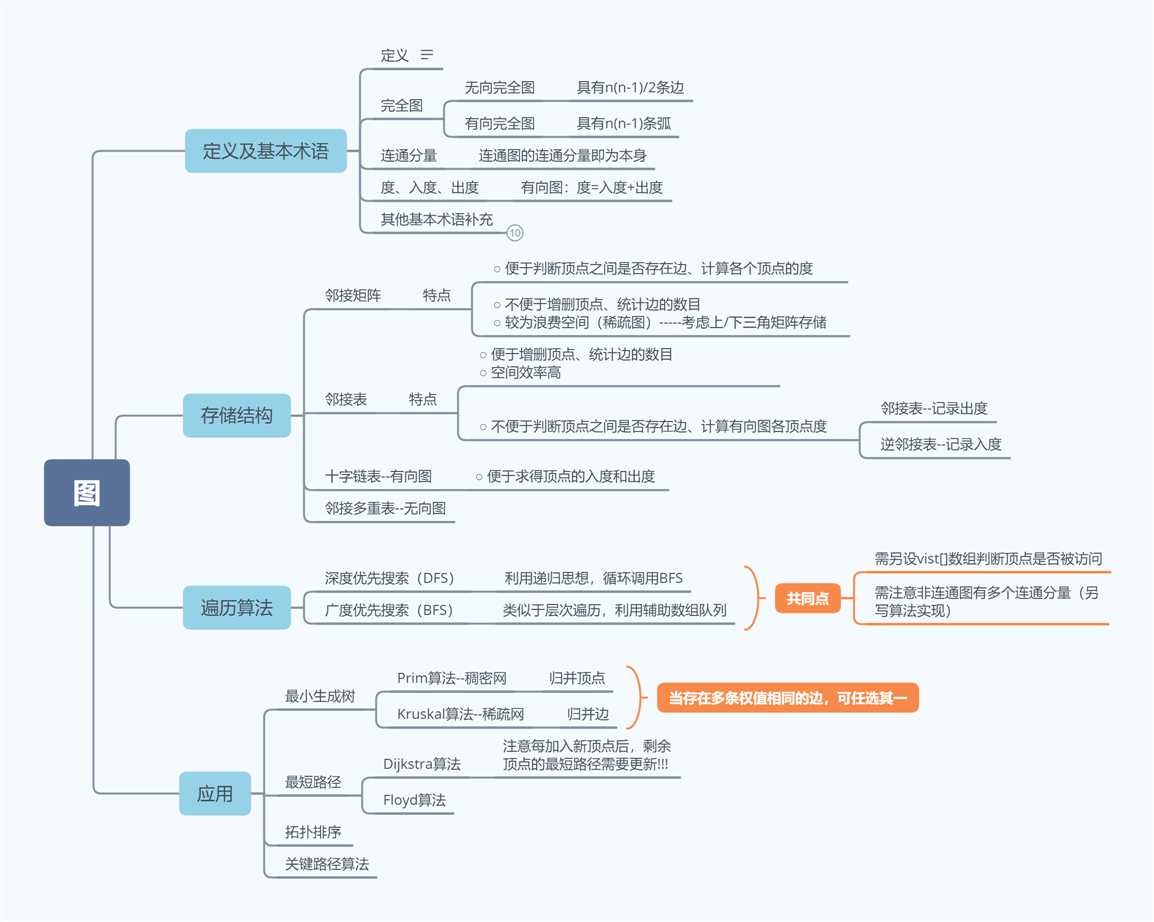
算法小结
1. 邻接矩阵存储

1 #define MVNum 100 //最大顶点数 2 typedef char VerTexType;//假设顶点的数据类型为字符型 3 typedef int ArcType;//假设边的权值类型为整型 4 5 typedef struct 6 { 7 VerTexType vexs [MVNum] ;//顶点表 8 ArcType arcs[MVNum][MVNum];//邻接矩阵 9 int vexnum, arcnum;//图的当前总顶点数和总边数 10 )AMGraph;
2. 邻接表存储

1 #define MVNum 100//最大顶点数 2 typedef char VerTexType;//假设顶点的数据类型为字符型 3 typedef int ArcType;//假设边的权值类型为整型 4 5 typedef struct ArcNode//边结点 6 { 7 int adjvex;//邻接点的位置 8 struct ArcNode *nextarc;//指向下一条边的指针 9 Otherinfo info;///和边相关的信息 10 }ArcNode; 11 12 typedef struct VNode//顶点 13 { 14 VerTexType data; 15 ArcNode *firstarc;//指向第一条依附该顶点的边的指针 16 }VNode,AdjList[MVNum];//AdjList表示邻接表类型 17 18 typedef struct//邻接表 19 { 20 AdjList vertices;//存储顶点信息的数组 21 int vexnum,arcnum;//图的当前总顶点数和总边数 22 }ALGraph;
3. DFS算法

1 void DFS_AM(AMGraph G, int v) 2 { 3 visited[v] = true;//访问过的顶点置为true 4 5 for(w=0; w<G.vexnum; w++)//依次检查邻接矩阵所在的行 6 if(G.arcs[v][w]!=0 && !visited[w]) //如果w是v的邻接点且w未访问 7 DFS_AM(G,w); //递归调用DFS_AM 8 }

1 void DFS_AL(ALGraph G, int v) 2 { 3 visited[v] = true;//访问过的顶点置为true 4 5 p = G.vertices[v].firstarc;//p指向v的边链表的第一个边结点 6 7 while(p!=NULL) //边结点不为空 8 { 9 w = p->adjvex; //w是v的邻接点 10 11 if(!visited[w]) //如果w未访问 12 DFS_AL(G, w);//递归调用DFS_AL 13 14 p = p->nextarc; //p指向下一个边结点 15 } 16 17 }
4. BFS算法

1 #include<queue> 2 void BFS(Graph G, int v) 3 { 4 visited[v] = true;//访问过的顶点置为true 5 6 queue<int> q;//辅助队列Q初始化 7 q.push(v);//v进队 8 9 while(!q.empty())//队列非空 10 { 11 int u = q.front();//队头元素出队并置为u 12 q.pop(); 13 for(int w = 0; w<G.vexnum; w++) 14 { 15 if(!visited[w] && G.arcs[u][w]==1) 16 {//w为u尚未访问的邻接顶点 17 visited[w] = true; 18 q.push(w)//w进队 19 } 20 } 21 } 22 }

1 #include<queue> 2 void BFS(Graph G, int v) 3 { 4 visited[v] = true;//访问过的顶点置为true 5 6 queue<int> q;//辅助队列Q初始化 7 q.push(v);//v进队 8 9 while(!q.empty())//队列非空 10 { 11 int u = q.front();//队头元素出队并置为u 12 q.pop(); 13 p = G.vertices[u].firstarc;//p指向u的第一个边结点 14 while(p != NULL) //边结点非空 15 { 16 w = p->adjvex; 17 if(!visited[w])//若w未访问 18 { 19 visited[w] = true; 20 q.push(w)//w进队 21 } 22 p = p->nextarc; //p指向下一个边结点 23 } 24 } 25 }
5.(补充)非联通图的遍历

1 //非连通图需遍历所有的连通分量,因此另需一个遍历函数 2 void Traverse(Graph G) 3 { 4 for(v=0; v<G.vexnum; v++) 5 visited[v] = false;//初始化visit数组(可以直接初始化或menset()函数) 6 7 for (v=0;v<G.vexnum;v++){ 8 if(!visited[v]) 9 DFS(G,v);//对尚未访问的顶点调用DFS算法 10 } 11 }
其他知识点小结
1. 使用邻接表存储无向图,为什么要足够稀疏才合算?
答:因为邻接表储存无向图的时候,有n个顶点就要创建n个链表,且每个链表都会存和本顶点相关联的顶点,故每一条边会被存两次,且每一个结点至少会有两个域存储数据。
2. 使用邻接矩阵a存储无向网络,若vi与vj之间不存在边,则a[i][j]值为多少?
答:若权值为正整数,可设为0或负数。若权值为整数,则可设为一个大于所有边权值的数。
3. 最小生成树不一定唯一,但是用算法来查找的最小生成树一般是唯一的(排除使用随机数计算的情况)
4. 重置visit[]数组(用于判断顶点是否被访问)
① for循环重置
②?memset函数重置(更简洁)

1 //适用于初始化、重新赋值以及清空等情况 2 //memset()函数在头文件string.h里 3 #include<string.h> 4 int visit[100]; 5 menset(visit, 0, sizeof(visit));//第一个参数是数组名,第二个参数是设置的值,第三个参数是数组长度
心得体会
1.图需要学习的基本术语较多,但可以大致了解一些比较重要的术语,对于其他的可以接触到再学以致用;
2.另外由于图定义时涉及到的成员变量较多,做题目的时候经常要对照着书本或者前面的代码确认是否写正确_(:з)∠)_;
3. 总体来说,目前对于图的应用的算法基本理解,但自己复现起来可能会生疏,此外感觉自己对于邻接矩阵的上手熟练程度远超于邻接表,可能对于链表的写法不够熟练....之后应该多回顾一下。
标签:lis arc 网络 cab list mvn 为什么 访问 play
原文地址:https://www.cnblogs.com/Function-F/p/13122930.html