标签:介绍 ima 维度 估计 颜色 输入 注意 lazy 进度
今天是2020年6月14号星期日。从这篇开始,发布时间就正常了。前边的文章是在寒假写好的,后来因为赶进度和整理小论文,没有及时整理。3月到6月,两个半月的时间做了些什么?真的好怕浪费了时间~《统计学习方法》这本书(第二版),大概在四月底就看个差不多了,半生不熟的好歹是通篇过了一遍,当然不止一遍,除了潜在狄利克雷分配。期间夹杂着手撕代码的过程,因为脑容量有限的原因,写代码的时候,又要把书面内容重新过一遍。就连发布,也要重新过一遍,把重要的地方加上不同颜色...于是这个假期,《统计学习方法》这本书的每个章节,不知道反反复复的过了多少遍,肯定不超过十遍...也就是看的多,不代表学的多...但是看了总归是看了,也比不看强...
CRF条件随机场~本节说难,挺难;说简单,也简单。为什么我觉得CRF和LR很像呢?可能有很多人在应用场景上反驳我,LR做数据分类问题,CRF是针对序列标注问题。我觉得像,提供一下几个观点(递进着看):
1.LR和CRF都是判别模型。这句话要从计算方式上来理解:LR是通过线性函数,对特征向量拟合不同的权值,最后加和的线性函数值作为sigmoid函数的输入,转换为概率值(对数几率)。CRF在公式(11.10)中,不,在更明显的公式(11.15)中,wkfk(y,x)对1->K加和。个人肤浅的理解:公式(11.15)就是对各个特征拟合不同的权值wk,加和的线性函数值作为某个“求概率公式”的输入。
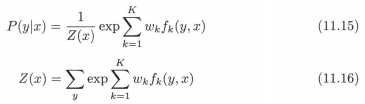
2.从观点1出发,思考一下“特征”。在LR中,“特征”很明显,就是特征向量的各个分量,相当于一个分量一个特征。LR拟合的w,其实就是看看每个特征分量对分类结果占什么样的贡献。在CRF中,“特征”是定义在最大团上的,抛去“最大团”“势函数”“特征函数”这些抽象概念,CRF的“特征”其实不就是定义在相互联系的两个节点上嘛?相当于“成对”构成一个特征。转移特征也好,状态特征也罢,线性链条件随机场不就限定了“特征”要产生在“成对”的关联关系上。然后,公式(11.15)告诉我,[权值×特征==》加和],CRF和LR计算线性函数值的方式没区别啊(区别在特征的定义上)。
3.从观点1出发,思考一下“概率的计算”。不知道大家有没有仔细思考LR中,第六章公式(6.6)分母位置的1是怎么计算的,或者为什么要在分母添加这一项。是不是可以理解为exp(0*wx)=1,这样能够把分母作为归一化项Z(x)看待。分母的1+exp(wx)看作Z(x)=exp(0*wx)+exp(1*wx),P(Y=1|x)=exp(1*wx)/Z(x),另一个类别Y=0的概率P(Y=0|x)=exp(0*wx)/Z(x),怎么样,香不香?这里不就是两个项的线性函数值进行了指数归一化。在这个角度上,看CRF的概率计算方式,公式(11.15)和公式(11.16)不就是多了几项嘛...多个项(K项)进行了归一化,把数值转换成了概率值,这这这,和softmax()指数归一化不就是一回事嘛...然后再考虑考虑为什么CRF中势函数是严格正的...
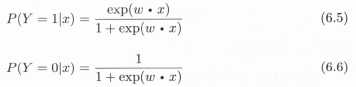
暂时先这三点,实际上都是围绕[判别模型]提出的。
GitHub:https://github.com/wangzycloud/statistical-learning-method
条件随机场
引入
书中对条件随机场CRF的描述是:给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场。先抛去“输出随机变量构成马尔可夫随机场”这个限定条件不看,该模型是条件概率模型,并且是一组随机变量,在另外一组随机变量条件下的条件概率模型。
组这个概念,限定了模型中发生作用的因素要产生在多个随机变量上。类似这样,形象不(仅代表个人理解哈~不能保证正确):

像示意图中表示的,如果一组随机变量之间,关系是散乱无序的,我们该怎样求解呢?各个组上随机变量的关系都发现不了,何谈寻找A组在B组条件下的条件概率分布?因此,考虑对输出组的随机变量施加限定条件。人类最常做的就是发现规律,总结经验。比如说,让输出组的随机变量两两之间产生联系,会不会简化问题?
于是,模型变成了这样。又或者,让输入组随机变量和输出组随机变量,都变成序列关系。这时,问题变成了由输入序列对输出序列预测的判别模型。具体的,让输出组随机变量构成马尔可夫随机场。需要的知识包括图与无向图、马尔可夫性、无向图模型的因子分解、团与最大团...
概率无向图
概率无向图模型,又称为马尔可夫随机场,是一个可以由无向图表示的联合概率分布。“马尔可夫随机场”正式出场了,简单讲它是一个联合概率分布,是由无向图表示的。想象无向图的样子,由结点和边构成,且边没有方向(无箭头)。深入一点,一个结点表示一个随机变量,如果两个结点之间有边关联,就认为这两个结点具有关联关系,并且是“相互关联”(无向边),相互产生影响。

可以看到,“有向变无向”这个操作,让限定条件变的更宽泛了,也就是让CRF的应用场景增多。当然,无向图不只是上图的线性序列关系。根据马尔可夫性的不同,概率无向图模型也有很多种类。接下来由图开始,具体介绍一下模型的定义。

看一下马尔可夫性,我的理解是这样:在无向图G上给定Cs(与集合C有关的一堆结点),As和Bs条件独立。As和Bs之间没有边关联,就算利用Cs作为结点把As和Bs连接了起来,两者仍然保持独立关系。
有三种类型,分别是成对马尔可夫性、局部马尔可夫性、全局马尔可夫性,具体定义较晦涩。如下:

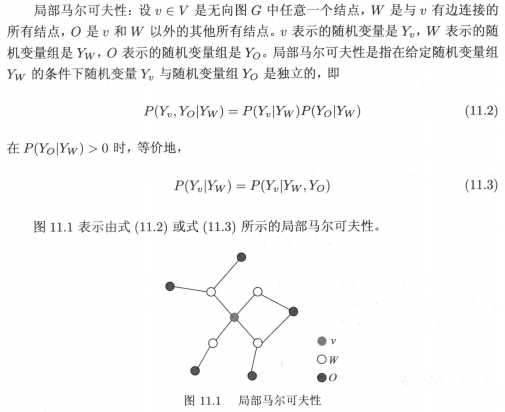

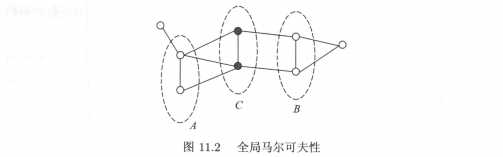
由以上马尔可夫性,概率无向图模型定义为:

有了概率无向图的定义,实际上我们更关心的是如何求解各个随机变量的联合概率分布。那么,对给定的概率无向图模型,我们能不能找到将整体的联合概率写成若干个子联合概率的乘积的方法?也就是将联合概率进行因子分解(类似:6=2×3,整数6可以分解成因子2乘以因子3),就能方便模型的学习与计算了。事实上,概率无向图模型最大的特点就是易于因子分解。这里留几个疑问,“整体的”变成若干个“子联合概率的”这句话,子联合概率我不是可以理解成“子集”的,这个子集要如何划分?我们知道,图结构动不动就会像渔网一样,横七竖八的全是连接边。
另外,联合概率的因子分解,不仅要能解决无向图上划分小子集的问题,还要保证各个小子集乘积的联合概率要等于整体的联合概率。
这里划分小子集的问题,由无向图上的“最大团”解决的,定义如下:
 例子中描述的,应该是挺清楚的,最大团中的任何两个结点均有边连接。于是,概率无向图模型的联合概率分布可以表示为其最大团上的随机变量的函数的乘积,这种操作称为概率无向图模型的因子分解。接下来,考虑联合概率如何计算。
例子中描述的,应该是挺清楚的,最大团中的任何两个结点均有边连接。于是,概率无向图模型的联合概率分布可以表示为其最大团上的随机变量的函数的乘积,这种操作称为概率无向图模型的因子分解。接下来,考虑联合概率如何计算。

不管整体的联合概率也好,子集的联合概率也好,无非是表示一大撮和一小撮随机变量的区别。问题在于,这个东西它是概率啊。怎么在图结构上体现概率啊...公式(11.15)和公式(11.16)给出了答案,对每个Yi(N个状态序列中的一个序列Yi)求分值,将各个“得分”归一化后的结果作为该无向图Yi的联合概率。实际上也就是每一个无向图Yi是所有状态序列中的一种情况,这个Yi的得分占所有情况的比例,就认为是Yi的联合概率。
这里Yi的得分,是如何反映的呢?可以从公式(11.15)看出,图中所有最大团上各个最大团势函数的乘积,作为Yi的得分。
串到CRF特征抓取的过程中,我认为这里的势函数,就是抓取最大团集合中的结点特征,并且是各个结点之间的关联特征。由于训练过程中拟合参数wk,所以这里只需要将每个特征作为正的“量”就可以了。势函数仅作标示“特征”的度量(metric),拟合的wk决定该特征对“得分”影响的正负、大小程度(对应开头的观点3)。
现在利用的这种方式,不是空穴来风,是有定理来保证的:

条件随机场的定义与形式
条件随机场是给定随机变量X条件下,随机变量Y的马尔可夫随机场。我们要用到的CRF指的是定义在线性链上的特殊的条件随机场,称为线性链条件随机场。一般情况下,在条件概率模型P(Y|X)中,Y是输出变量,表示标记序列;X是输入变量,表示观测序列。这里,我们也把标记序列称为状态序列。在学习时,利用训练数据通过极大似然估计或正则化的极大似然估计得到条件概率模型;预测时,对于给定的输入序列x,求出条件概率模型最大的输出序列y。
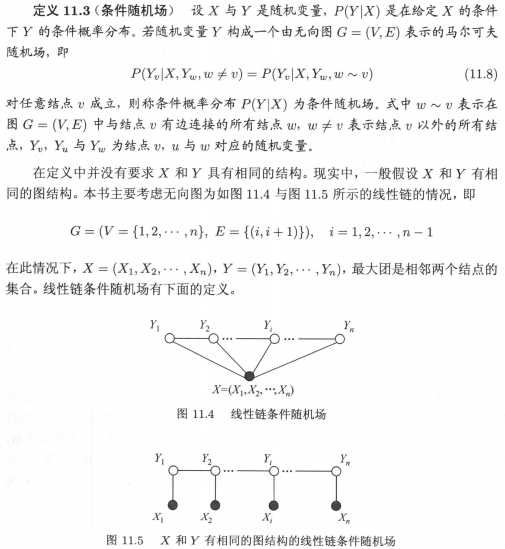
我认为在给定输入序列X的条件下,计算输出序列Y的条件概率(且序列Y构成线性链条件随机场)的场景是与图11.4相符合的。文中描述的,现实中一般假设X和Y有相同的图结构,形如图11.5这样,这就好像对模型进行了简化,让模型更容易实现。换一个角度看,图11.4中的X表达的是输入序列整体对输出序列Y的影响,具体到如何产生影响,如图11.5表达的这样,输入序列X的每个分量Xi,与相同时刻的Yi相互影响。
这里留两个疑问,(Xi,Yi)的相互影响关系,会不会传递到t时刻?与时刻t有没有关系?
看一下线性链条件随机场的具体定义:
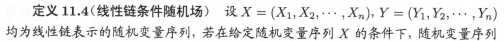

图示如下,公式(11.9)实际上表达了:马尔可夫性规定Yi(Y3)只与相邻的结点有关联关系(蓝框代表等式左侧,红框代表等式右侧)。
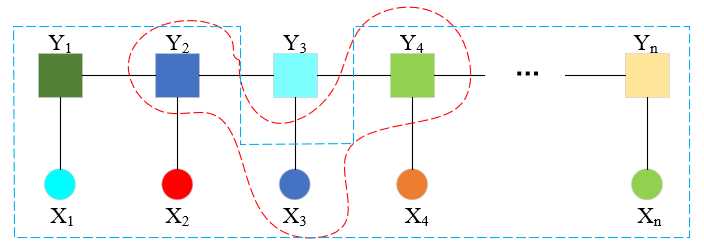
根据定理11.1,可以给出线性链条件随机场P(Y|X)的因子分解式,各因子是定义在相邻两个结点(最大团)上的势函数。两个疑问的解答,相信后面部分的描述中可以找到答案。接下来看一下条件随机场的三种形式。
1)条件随机场的参数化形式

该基本形式,表示给定输入序列x,对输出序列y预测的条件概率。实际上现在的具体定义,就是把最大团、势函数、概率求解等概念落实下来,变成可以量化的东西。公式(11.11)为归一化项,相当于把Y的每种情况(各种Y序列)考虑到,作为求概率时的分母(每种情况下,各个得分加和)。在某个情况Y下,计算该Y的概率,需要先得到所有势函数构成的特征和,也就是“得分分值”。
这里的特征来自两部分,yi-1与yi横向上的转移特征tk(·)和yi与x竖向上的状态特征sl(·)。
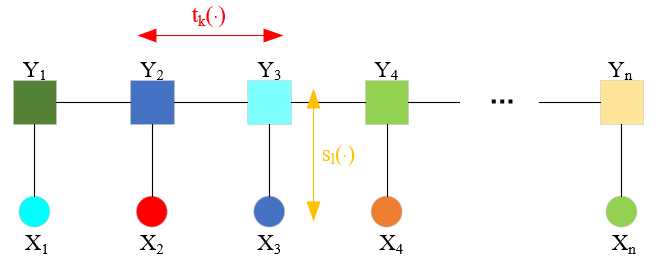
看一下具体定义:

这里tk和sl的取值,类似于最大熵模型中特征函数的定义。我的理解,取1或者0,是标记这个特征有还是没有。至于此时该特征的贡献是大是小,是正是负,这取决于模型训练时拟合的参数情况(λ、μ)。
举个例子,看下计算时的具体过程:

该标记序列y=(y1,y2,y3)的非规范化概率,实际上就是通过存在的特征×对应权重,然后加和。符合[权值×特征==》加和]这个方式。
2)条件随机场的简化形式
注意到条件随机场公式(11.10)中同一个特征在各个位置都有定义,可以对同一个特征在各个位置求和,从而将局部特征转化为一个全局特征函数。这样就可以将条件随机场写成权值向量和特征向量的内积形式,也就是现在要描述的简化形式。实际上,这更进一步贴近了[权值×特征==》加和]这种方式。
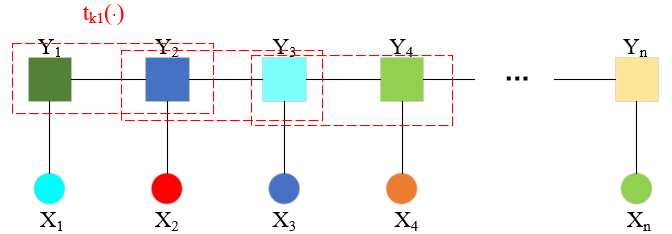
如上图所示,假设每个位置i都有这个局部特征(没有该特征的话,特征值为0),每个i都要针对这一个局部特征求一个参数,这个工作量似乎有点大,并且重复。那么,是不是可以把该局部变量上升到全局特征,每个局部位置特征值加和,让这一个特征在全局上学习一个权重参数。一来减少没必要的参数估计,二来可以把重点放在“特征”的增加和估计上。

这里公式(11.13)表明了全局特征是通过各个位置i的局部特征加和得到的。
 接下来,用向量形式进行表示:
接下来,用向量形式进行表示:

这样就得到了条件随机场的简化形式。经过知识点细化,再抽象,看CRF公式(11.19)和公式(11.20)和LR中的公式(6.5)和公式(6.6)多像。各个特征的线性函数值(得分),通过指数归一化转化成概率,学习的过程拟合各个参数。
3)条件随机场的矩阵形式
先看定义:

这里先记一个要点,对每个标记序列引进特殊的起点和终点状态标记,这时标注序列的概率Pw(y|x)可以通过矩阵形式表示并有效计算。划重点:引进特殊起点和重点标记之后,才可以通过矩阵形式计算。

不知道怎么分析这个地方,现在从以下几个问题开始:
①公式(11.21)中Mi的下标i和yi的下标i是否表示同一个意思?
我认为这两个下标i指的不是同一个意思,yi的i表示该矩阵中状态的取值;Mi中的i表示第i个矩阵,实际上每个位置都有对应的矩阵。同时矩阵的维度是M×M维的,因为yi可以取到M个状态(yi有M个状态,yi-1的某个状态可以转移到M个中任意一个,yi-1有M个状态,所以转移有M×M种)。例M2(1,3)表示在状态序列的第2个位置上(t=2),由t=1时刻的“状态1”转移到t=2的“状态3”的非规范化概率。
②Mi中的元素是怎么计算的,是什么?
计算方式见公式(11.22)和公式(11.23)。我先想到的是,Mi矩阵为yi-1到yi的转移矩阵,每个时刻yi都是M种状态,转移也都是yi-1到yi这些转移方式,计算方式都由公式(11.23)计算。那么,不同的Mi之间的区别是什么呢。我的理解是针对不同的时刻t、不同的x,特征函数是否存在和相应的权值大小,决定了Mi不同。
③公式(11.24)的分子部分n+1个矩阵的适当元素的乘积,是什么?
仔细看一下CRF的简化形式中公式(11.15)的分子部分,利用公式(11.13)对i进行展开,有:
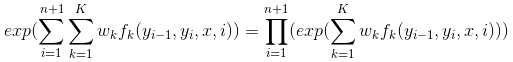
是不是就变成了公式(11.24)的分子部分n+1个矩阵的适当元素乘积的形式。也就是说,CRF的矩阵形式来源于简化形式,至于为什么会有这种方式,我觉得是便于计算吧,下边前后向算法会用到这种形式。
④公式(11.25)规范化因子,是什么?
看上去是对所有序列的非规范化概率的总和。其实追根究底④这个问题是想知道矩阵运算在这里计算的是什么。
综上,条件随机场矩阵形式的要点有:
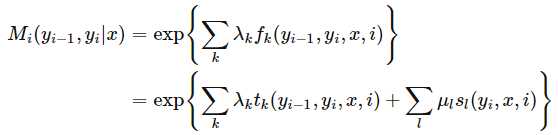
以2×2的Mi矩阵为例(例11.2),具体表示如下:
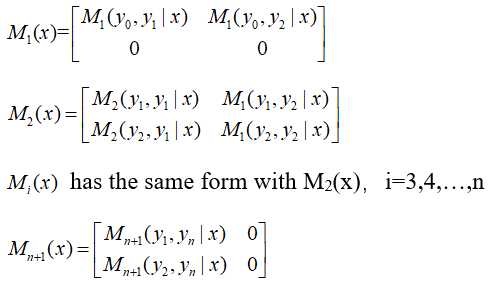
看一下例11.2:


以状态序列(1,2,1)为例:
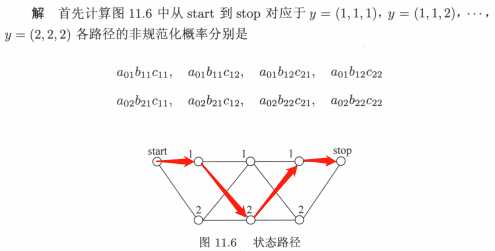
解析如下:
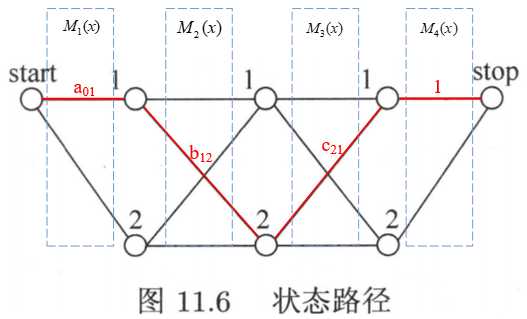
接下来看一下求规范化因子的过程:

上面提到的问题④,n+1个矩阵连乘后,得到的结果仍然是M×M维的。但第1行第1列的元素,正好是所有路径上的非规范化概率之和。
了解完概率无向图、条件随机场的定义和各种表示方法之后,与隐马尔可夫模型类似的,接下来介绍条件随机场的3个基本问题:概率计算问题、学习问题、预测问题。
条件随机场的概率计算问题
与隐马尔可夫模型类似,引进前向-后向向量,递归的计算概率(递归的计算过程是非常不同的)。

先看前向计算过程。注意CRF作为无向图模型,抛去了HMM的方向性,我们要从矩阵乘法的角度进行分析。仔细看一下公式(11.28),转换成矩阵语言如下(以m=5为例,这里将时刻的下标标记为t,用来区分yi的状态和时刻t:αi->αt,Mi->Mt):

具体到转换过程中(考虑矩阵乘法的过程):
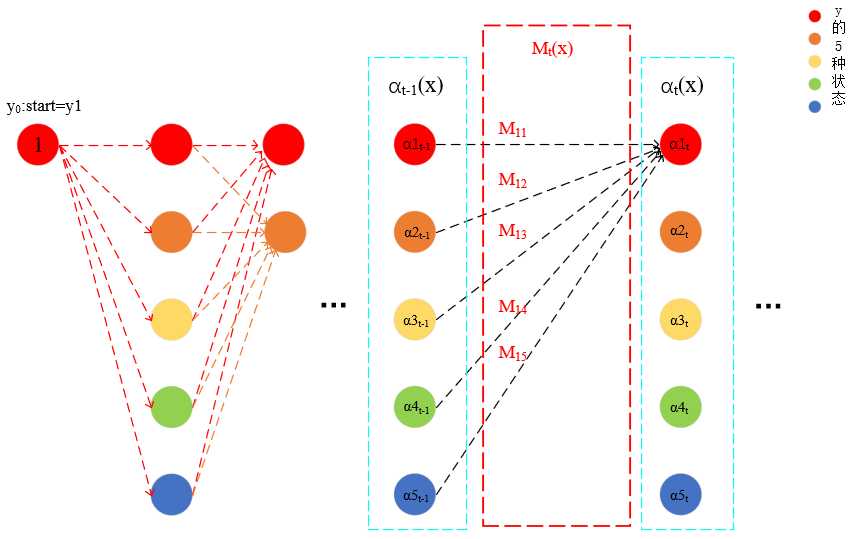
可以看到,α1t的得出,是结合了t-1时刻各个αi的结果。再来理解一下“αt(yi|x)表示在位置t的标记是yi并且从1到t的前部分标记序列的非规范化概率”这句话,见下图:
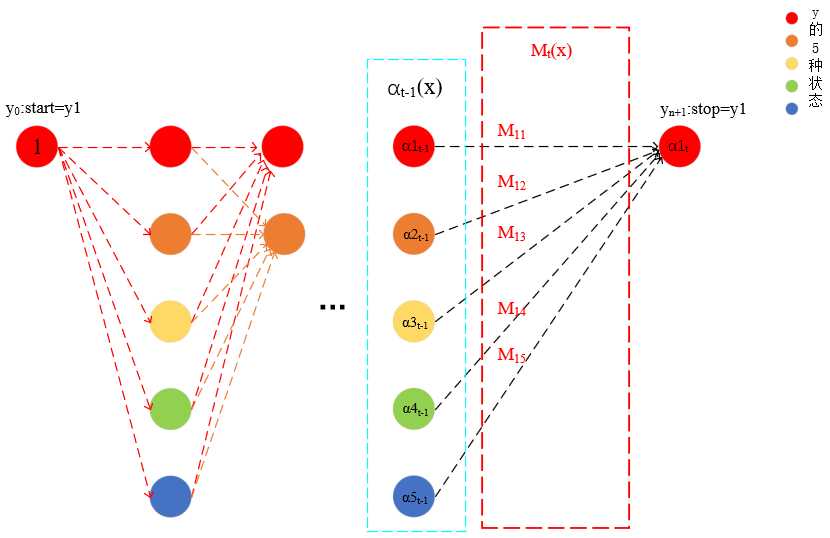
实际上,t时刻α向量中的某一个分量,αi可以视作终点状态取yi时的非规范化概率,并且这个概率是1->t时刻的整个过程中,所有可能序列的非规范化概率之和(从start到stop所有路径上的非规范化概率之和)。如图中,α1t也就是从start=y1到stop=y1过程中,所有可能序列的非规范化概率之和。因此,每个αi是start=y1到stop=yi的规范化因子Zi。这样就能看出与HMM特别不同了,一个应用矩阵乘法,一个应用条件概率公式。
我理解的大概就是这个样子,不知道能不能写清楚,接下来看下后向算法的计算过程。从公式(11.31)开始:
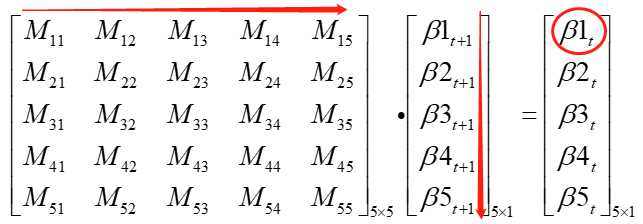
具体到转换过程中(考虑矩阵乘法的过程):
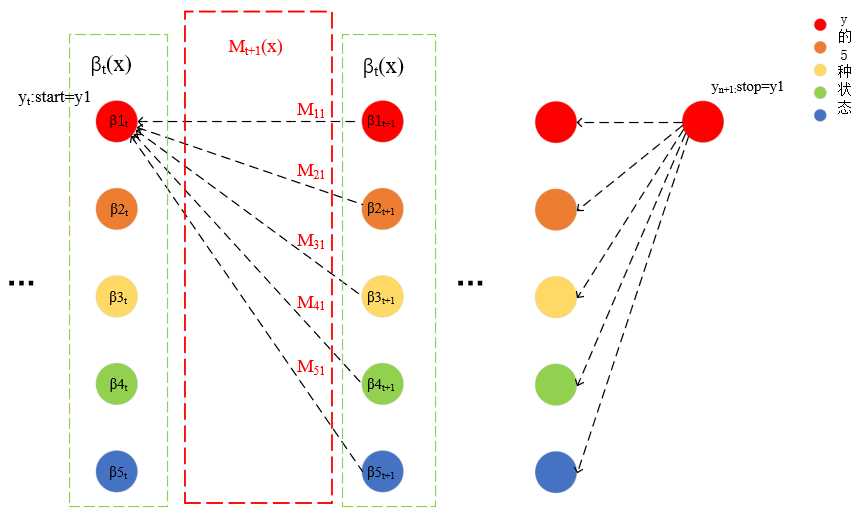
于是,βt(yi|x)可以表示从t时刻yt:start=y1到yn+1:stop=y1,所有路径上的非规范化概率之和(共T-t个结点状态的序列)。前向算法也好,后向算法也好,这里的箭头指向仅表示乘的方向,不是有向图结构。
与HMM类似的,接下来看几个概率计算。

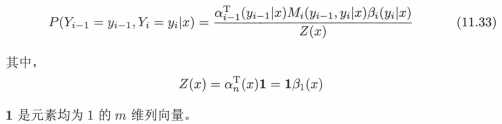
公式(11.32)和公式(11.33)还是好理解的,看一下示意图:
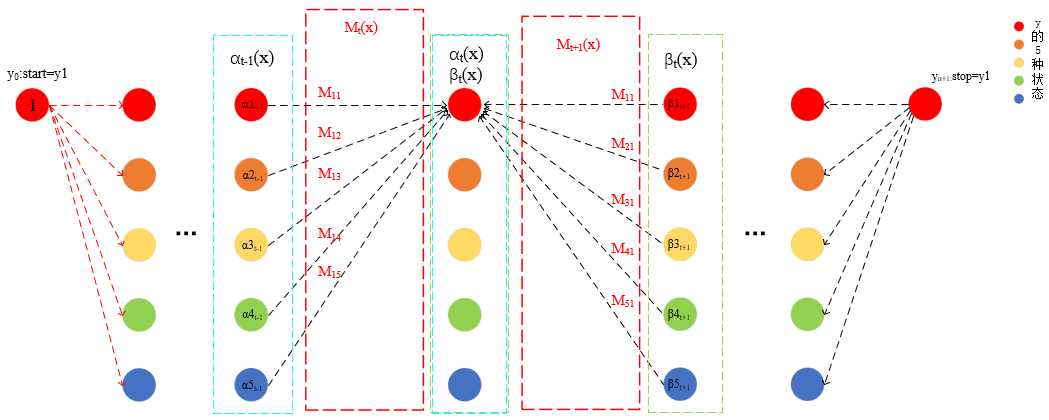
通过示意图,先来看一下Z(X),Z(X)既可以通过前向向量,又可以通过后向向量来求。实际上,不管前向向量αn也好,后向向量β1也好,Z(X)的计算矩阵过程,实际上是把m个值加和,也就是得到所有状态序列的规范化因子。
分开看公式(11.32)分子部分,我觉得是两个值(α、β)进行了相乘。第一个α值,代表了从0时刻start=y1到t时刻stop=yi的非规范化概率;第二个β值,代表了从t时刻start=yi到n+1时刻stop=y1的非规范化概率。公式(11.33)是类似分析方法。
再来看一下几个期望的计算,就不具体分析了:


条件随机场的学习问题
学习问题实际上讨论的是在给定训练数据集上估计模型参数的问题。条件随机场模型实际上定义在时序数据上的对数线性模型(是不是与LR像),学习方法包括极大似然估计等,具体的有改进的迭代尺度法IIS、梯度下降法及拟牛顿法。
具体的方法目前先不弄了(有大概了解,但了解的程度,不足以写出来),赶赶刷题的进度去了...等找着工作了,准备毕业的时候再把这些方法整理上~
话说这章的代码没写,因为不会...不知道从什么地方下手。
条件随机场的预测问题
同HMM,大名鼎鼎的维特比算法。
PASS
标签:介绍 ima 维度 估计 颜色 输入 注意 lazy 进度
原文地址:https://www.cnblogs.com/wangzycloud/p/13081342.html