标签:深度优先 queue oid for循环 lazy 并且 方法 开始 style
图
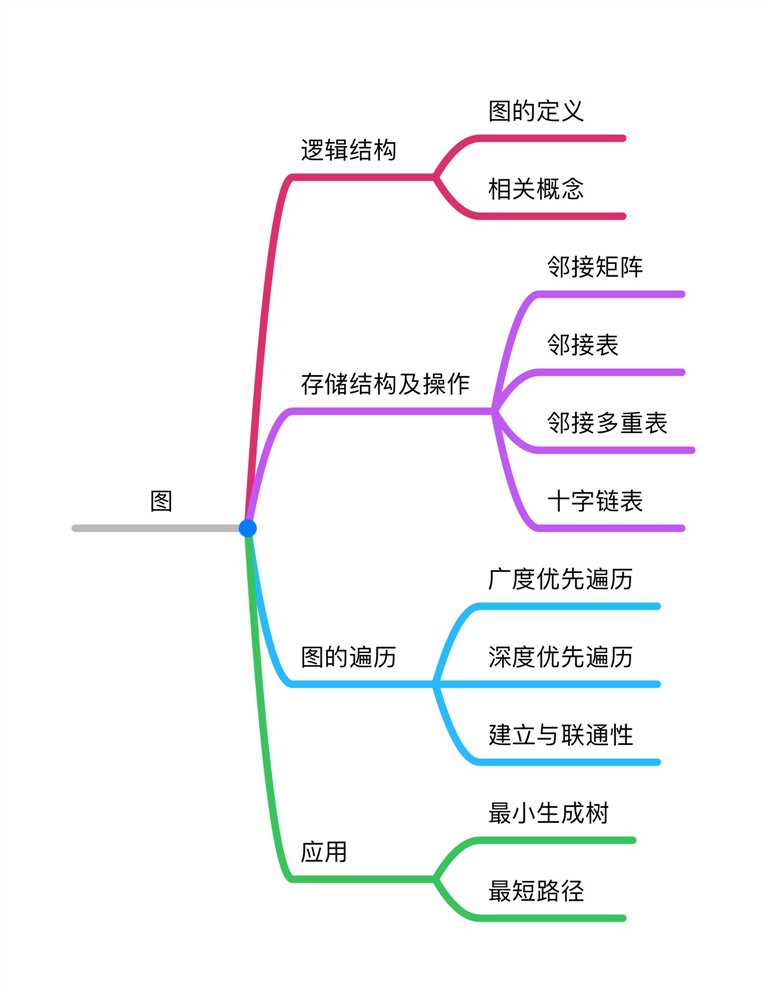
逻辑结构
图的定义
图G由顶点集V和边集E组成,记为G=(V,E),其中由V(G)表示图中G中的顶点的有限非空集;E(G)表示图G中顶点之间的关系(边)集合(图不能为空)
|V|表示图中顶点个数也称图的阶;|E|表示图中边的条数
相关概念
无向图&有向图
无向边:v-w 无序对(v,w)=(w,v)v,w互为邻接点
有向边:v->w 有序对<v,w> v邻接到w,或w邻接自v
简单图&多重图
简单图:无重复的边,不存在节点到自身的边
多重图:存在重复边,或存在节点到自身的边
完全图
无向完全图:任意两个顶点之间都存在边,n个顶点有n(n-1)/2条边
有向完全图:任意两个顶点之间都存在方向相反的弧,n个顶点有n(n-1)条边
连通&强连通
连通:若从顶点v到顶点w有路径存在,则称v和w是连通
强连通:若从顶点v到顶点和顶点w到顶点v都有路径存在,则称v和w是强连通
N个顶点的连通图/强连通图至少有多少条边:N-1 / N
图的存储结构
邻接矩阵
定义:结点数为n的图G=(V,E)的邻接矩阵A是n*n的,将G的顶点编号为v1,v2,…,vn(数组下标),若<vi, vj>属于E,则A[i][j]=1,否则为0。如果边有权重w,则A[i][j]=w
空间复杂度为O(n^2),适用于稠密图
设图G的邻接矩阵为A,矩阵运算A……n的含义:A^n[i][j],表示从顶点vi到顶点vj长度为n的路径条数
邻接表
为每一个顶点建立一个单链表存放与它相邻的边
顶点表:采用顺序存储,每个数组元素存放顶点的数据和边表的头指针
边表:采用链式存储,单链表中存放与一个顶点相邻的所有边,一个链表结点表示一条从该顶点到链表结点顶点的边
若G为无向图,存储空间为O(|V|+2|E|),若G为有向图,存储空间为O(|V|+|E|),更适用于稀疏图(邻接表不唯一)
十字链表
存储所有顶点的出边以及入边,针对于有向图
邻接多重表
边表结点同时存储一条边的两个顶点的相关信息,针对于无向图
图的遍历
深度优先搜索
存储:栈+辅助标记数组visited[]
算法思路:
首先访问起始顶点v;
接着访问v的各个未被访问过的邻接顶点wi;
然后访问与wi邻接且未被访问过的任意顶点ui;
若wi没有邻接且未被访问过的顶点时,退回到它的上一层顶点v;
重复2、3、4步骤直至所有顶点都被访问过。
空间复杂度:O(|V|) 时间复杂度:邻接矩阵O(|V|^2) 邻接表O(|V|+|E|)
void DFS(int v, int n) { if (!visited[v]) { visited[v] = true; cout << v << " "; for (int i = 0; i < n; i++) if (g[v][i] && !visited[i]) DFS(i, n); } }
广度优先搜索
存储:队列+辅助标记数组visited[]
算法思路:
首先访问起始顶点v;
接着依次访问v的各个未被访问过的邻接顶点w1,w2,…,wi;
然后依次访问w1,w2,…,wi的所有未被访问过的邻接点;
重复2、3步直至所有顶点都被访问过。
空间复杂度:O(|V|) 时间复杂度:邻接矩阵O(|V|^2) 邻接表O(|V|+|E|)
邻接矩阵的广度优先生成树唯一,邻接表的不唯一
void BFS(int v, int n) { queue<int> q; visited[v] = true; q.push(v); while (!q.empty()) { v = q.front(); q.pop(); cout << v << " "; for (int i = 0; i < n; i++) { if (g[v][i] && !visited[i]) { q.push(i); visited[i] = true; } } } }
在无向图中,调用遍历函数(BFS/DFS)的次数为连通分量的个数
应用
最小生成树
性质:
1) 最小生成树不一定唯一,即最小生成树的树形不一定唯一。当带权无向连通图G的各边权值不等时或G只有结点数减1条边时,最小生成树唯一
2) 最小生成树的权值是唯一的,且是最小的
3) 最小生成树的边数为顶点数减1
Prim算法
适用于稠密图
Kruskal算法
堆排序 并查集
适用于稀疏图
最短路径
Dijkstra算法
辅助数组:s[]:标记已计算完成的顶点 dist[]:记录从源点v0到其他各顶点当前的最短路径长度 path[]:记录从最短路径中顶点的前驱顶点,即path[i]为v到vi最短路径上vi的前驱顶点
算法思路:
1) 初始化数组
2) 从顶点集合V-S中选出vj,满足dist[j]=Min{dist[i] | vi∈V-S},vj就是当前求得的最短路径的终点,将vj加入S
3) 修改此时从v0出发到集合V-S上任一顶点vk最短路径的长度;
若dist[j] + arcs[j][k]<dist[k]
则令dist[k]=dist[j] + arcs[j][k]; path[k]=j;
Floyd算法
算法思路:
递归产生一个n阶方阵序列A(-1), A(0), A(1), …, A(n-1)
A(k)[i][j]:顶点vi到vj的最短路径长度,且路径经过顶点的编号
递推方法:A(k)[i][j]=Min{A(k-1)[i][j], A(k-1)[i][k] + A(k-1)[k][j]}, k=0, 1, …, n-1
————————————————————
6.2个人小测
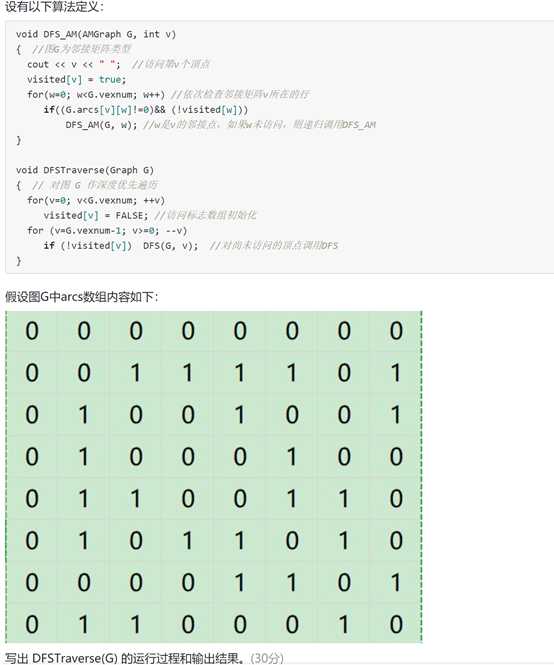
1)进入DFSTraverse的第一个for循环:
Visited[]全为F
2)进入第二个for循环
1. 进入DFG(G,v)(v=G.vesnum-1=7),输出7,visited[7]=true进入DFG(G,w)(w=1)
2.输出1,visited[1]=true,进入DFG(G,w)(w=2)
3.输出2,visited[2]=true,进入DFG(G,w)(w=4)
4. 输出4,visited[4]=true,进入DFG(G,w)(w=5)
5. 输出5,visited[5]=true,进入DFG(G,w)(w=3)
6. 输出3,visited[3]=true,此时第三行的1、5元素都已经访问过,返回上一个调用点
7. v=6,进入DFG(G,v)(v=6),输出6,visited[6]=true
8. 此时visited中除了0的所有元素都为true,回到DFSTraverse函数,不断- -v直至v=0,进入DFG(G,v)(v=0),最后输出0,visited[0]=true,结束调用
————————————————————
总结:图这一章节不同于其他章节的地方在于侧重算法理解,而不是实际代码的呈现(下个学期的算法课程才会具体讲)。而且算法这个东西是需要花时间去理解的,我目前能够最快理解算法的方式就是按照书上的样例去手动操作一遍,会比干看来的轻松很多,而且可以发现很多问题。6.8的时候晓梅老师布置了写最短路径实现过程的作业,开始对照ppt很快写完了,结果晚上飞扬来问我为什么第二个更新为1的结点不是2,我才发现我理解成了顺序访问数组,这是错误的。后来提交完晓梅老师给的批改建议是要将前驱节点按整型存储而不是字符型,所以手动操作算法实际上就是快速发现对算法不理解的地方并改正的过程。其次就是遍历算法的重要性,前几章老师也反复强调遍历要熟练掌握并且会写代码,这一章也是这样的,几乎所有对于图的具体操作都要建立在遍历的基础上,所以在本学期的数据结构课程中,遍历的代码掌握程度需要高于其他算法。
标签:深度优先 queue oid for循环 lazy 并且 方法 开始 style
原文地址:https://www.cnblogs.com/cmlearning/p/13124414.html