标签:技术 两种 后缀 for 方法 print 操作 span font
0。-4 和 4 交换,\(\{-2,11,4,13,-5,-2, -4\}\),最大子段和为11 + 4 + 13 = 28。先说错误的做法,不少同学直接搬运了网上的题解,并完美的ac了这道题,说句实话我是看了半天才明白其做法,对于最关键的地方一句显然,让人实在是无法理解。附上这些搬运工们的题解链接
做法的核心就是:显然sum[r]应该越大越好,就这么一句话就把枚举区间的时间效率由\(O(n^2)\)降到了\(O(n)\)。但这个显然没有找到一个合理的证明,还好找到了一组数据能够证明其错误,下面就附上错误做法和数据。
错误Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;
///formula : sum[r] - sum[l - 1] - min[l,r] + max(max[1,l - 1],max[r + 1,n])
int n;
ll sum[50005];
int s[50005];
int lmax[50005],rmax[50005];
int main() {
while(~scanf("%d",&n)) {
for(int i = 1;i <= n;i ++) {
scanf("%d",&s[i]);
sum[i] = sum[i - 1] + s[i];
}
for(int i = 0;i < n;i ++) {
lmax[i + 1] = max(lmax[i],s[i + 1]);
rmax[n - i] = max(rmax[n - i + 1],s[n - i]);
}
int maxi = n;
ll sumr_min,ans = 0;
for(int i = n;i >= 1;i --) {
if(sum[i] >= sum[maxi]) {
maxi = i;
sumr_min = sum[i] - s[i];
}
sumr_min = max(sumr_min,sum[maxi] - s[i]);
ans = max(ans,sumr_min - sum[i - 1] + max(lmax[i - 1],rmax[maxi + 1]));
}
printf("%lld\n",ans);
}
return 0;
}
/*
input
10
1 -100 1 100 100 100 -1000 2 3 4
output
311
*/
希望盲目copy的同学们引以为戒,可以借鉴,但一定要理解,不然就会闹出大笑话了!
正确做法:,任然是错误做法
这个车翻的有点猝不及防,才义正言辞的批评了一通 \(\Uparrow\) ,这个报应来得太快了,还好,代码是我写的,我只是没脑子(……),同学们头脑在线,这个老姚很欣慰!
交换操作,有以下三种情况:
显然,情况1,2交换后不影响最大子段和结果,所以我们只需考虑情况3。
对情况3,子段外的被交换的元素也有两种情况。
假设 \(a_i\) 是最大子段和中需要交换的元素,我们需要从子段左侧去找一个最大数,最大数好找,我们只需预处理出,\(O(1)\)的效率就能找到,关键是如何找到子段的左边界。
对情况1,如果我们能求出包含 \(a_{i-1}\) 最大后缀和,然后把 \(a_i\) 追加到后面即可,我们有多种方法\(O(n)\) 的预处理出结果和包含 \(a_{i-1}\) 的后缀的左边界,这样就确定了区间的左边界,然后再左边界左边找到最大的元素和啊\(a_i\) 进行交换即可。
对情况2,同上面类似,如果我们能求出包含 \(a_{i+1}\) 最大前缀和,右边界,这样就确定了区间的右边界,然后再右边界右边找到最大的元素和啊\(a_i\) 进行交换即可。
然后从这两种情况中去较大者。
如下图,\(dp_1[i-1]\) 以\(a_{i-1}\) 结尾的最大子段和,\(L\)是其左边界,\(dp_2[i+1]\)表示以\(a_{i+1}\)开始的最大子段和,\(R\) 是其右边界。所以我们只需从 区间\([1,L)\),或区间\((R,n]\)找到最大的和 \(a_i\) 交换即可。
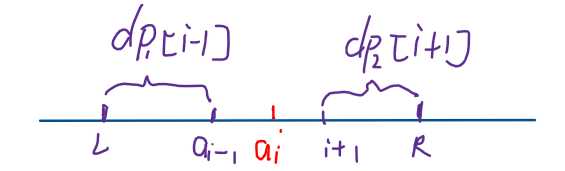
错误 Code
#include <bits/stdc++.h>
typedef long long LL;
const int maxn = 5e4+5;
const LL Inf=0x3f3f3f3f3f3f3f3f;
LL a[maxn],dp1[maxn],dp2[maxn];//dp1[i]以a[i]结尾的最大子段和,dp2[i]表示以a[i]开始的最大子段和
LL L[maxn],R[maxn],Lmax[maxn],Rmax[maxn];//L[i]以a[i]结尾的最大子段和的左边界,R[i]类似。
void Solve(){
int n;scanf("%d",&n);
for(int i=0;i<=n;++i)//Lmax[i]表示1~i的最大值,Rmax[i]表示i~n的最大值。
Lmax[i]=Rmax[i]=-Inf;
for(int i=1;i<=n;++i){
scanf("%lld",&a[i]);
Lmax[i]=std::max(a[i],Lmax[i-1]);
if(dp1[i-1]+a[i]>0){//存在包含a[i]的结果为正的子段和
dp1[i]=dp1[i-1]+a[i];
if(dp1[i-1]==0)L[i]=i;//只选a[i]自己
else L[i]=L[i-1];//a[i]并到以a[i-1]结尾的最大子段中
}
else L[i]=-1;//dp1[i-1]+a[i]<=0就什么都不选,为空
}
Rmax[n+1]=-Inf; //如果a[n]为负,如果Rmax[n+1]=0,那求出的Rmax[n]=0,是错误的。
for(int i=n;i>0;--i){//倒序求以a[i]开始的最大子段和
Rmax[i]=std::max(a[i],Rmax[i+1]);
if(dp2[i+1]+a[i]>0){
dp2[i]=dp2[i+1]+a[i];
if(dp2[i+1]==0)R[i]=i;
else R[i]=R[i+1];
}
else R[i]=-1;
}
LL ans=0;
L[0]=R[n+1]=-1;//0不存在左边界,n+1不存在右边界
for(int i=1;i<=n;++i){
LL x=0;
int l=i,r=i;//l,r记录区间的左右边界
if(L[i-1]!=-1){x+=dp1[i-1];l=L[i-1];}//如果存在以a[i-1]结尾的大于0最大子段和
if(R[i+1]!=-1){x+=dp2[i+1];r=R[i+1];}//如果存在以a[i+1]开始的大于0最大子段和
ans=std::max(ans,x+std::max(Lmax[l-1],Rmax[r+1]));
}
printf("%lld\n",ans);
}
int main(){
Solve();
return 0;
}
/*
4
-2 -4 1 -1
上面代码过不了下面的样例
错误的愿因是需要交换的a[i]向左扩展并不一定是包含a[i-1]的最大子段和
6
100 -1 1 -10 1 1
*/
正确做法
数学比较差,先盗个链接,容我仔细琢磨透了仔细给大家讲讲:https://blog.csdn.net/zlh_hhhh/article/details/78176629
标签:技术 两种 后缀 for 方法 print 操作 span font
原文地址:https://www.cnblogs.com/hbhszxyb/p/13130945.html