标签:二维空间 空间 弧度 之间 角度 没有 body int strong
之前在学习路径追踪的时候没有去细究里面的光学理论,最近趁着有时间把闫令琪老师的计算机图形学课程(万万没想到在B站上也可以学习!)辐射度量学的内容又仔细学习一遍,也算是打下了路径追踪的理论基础。
辐射度量学提供了一组基本的物理量用来测量光辐射,这些物理量也就成为了计算机图形学中重要的基本概念,如下表所示:
| 英文名 | 中文名 | 单位 | 符号 |
|---|---|---|---|
| radiant energy | 辐射能量 | J | Q |
| radiant flux | 辐射通量 | W | Φ |
| irradiance | 辐射照度 | W/m^2 | E |
| radiant intensity | 辐射强度 | W/sr | I |
| radiance | 辐射亮度 | W/(m^2 * sr) | L |
后面将对它们依次进行介绍。
辐射能量(radiant energy)代表的是电磁辐射的量度,单位为焦耳(J)。每个光子都携带着一定的能量,这个能量正比于它的频率v,也就是:
Q=hv
其中h为普朗克常数。由于频率决定着光的颜色,我们也就可以说,蓝光要比红光携带更多的能量。
而辐射通量(radiant flux)指的是单位时间上的辐射能量。它的单位为W(也就是瓦特),数学定义如下:
Φ = dQ/dt
辐射强度,要首先介绍立体角。那立体角是什么呢?
立体角代表的是三维空间上的角度。为了帮助理解,我们可以想象一下二维空间的角度,如下图所示:
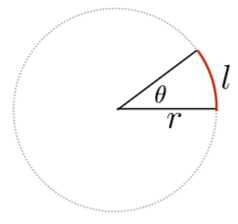
这个二维圆上,它的角度为θ,半径为r,弧度为l,那么:
θ=l/r。整个圆的角度为2π。
拓展到三维空间,立体角就是三维空间的“θ”,被定义为Ω。那么该片角度所涉及到的球的面积就是A,如下图所示:
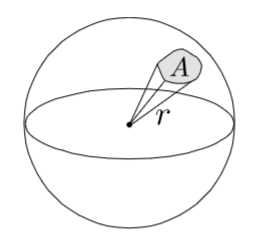
可以算得:
Ω = A/r^2
对整个球,它的立体角角度为4π。
下图展示了立体角的积分过程:
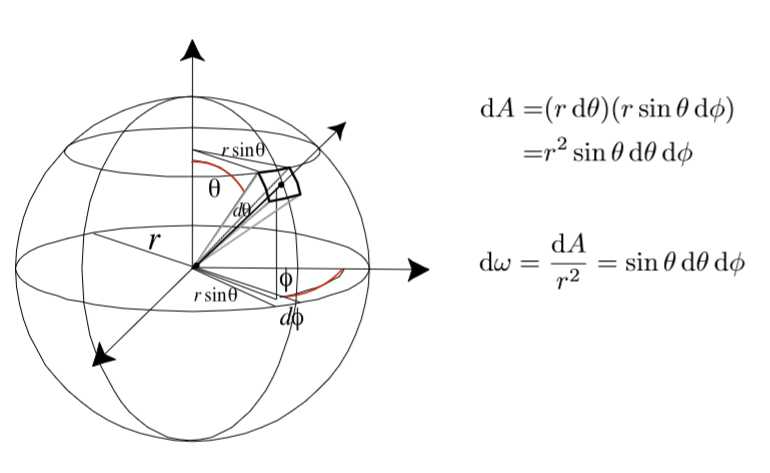
因为三维的位置,按照球坐标系来算的话由r、θ、φ三个参数来控制,根据上面提到的弧长和角度的关系,可以算得在dθ和dφ的情况下,dA的计算,再通过面积和立体角的关系来推得立体角的微分dω即可。
知道了立体角的概念后,就可以定义辐射强度(radiant intensity)为单位立体角的辐射通量:
I = dΦ/dω
辐射照度指的是在单位面积上的辐射通量:
E = dΦ/dA
而辐射亮度指的是在单位面积、单位立体角上的辐射通量:
L=d^2Φ/dωdAcosθ
值得注意的是,这里的cosθ指的是面的法向和光源之间的夹角,因此上面提到的面积其实是单位垂直面积。
其实用辐射照度就可以解释为什么距离光源越远接收到的能量越少:
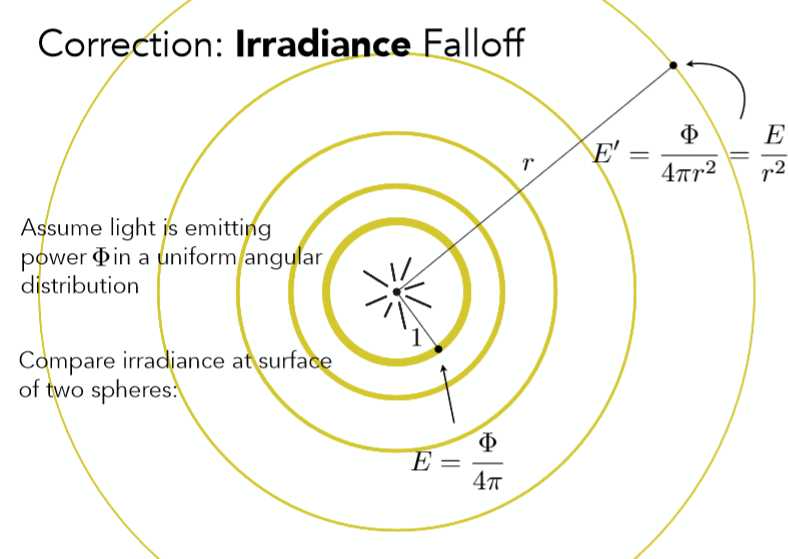
如上图所示,因为辐射通量Φ是固定的,随着r越来越远,其面积也就越来越大,因此单位面积所接收到的能量也就越来越少,这是符合常识的。
标签:二维空间 空间 弧度 之间 角度 没有 body int strong
原文地址:https://www.cnblogs.com/wickedpriest/p/13132337.html