二进制矩阵中的最短路径（力扣第1091题）

标签：合作   binary   阻塞   选择   组成   ret   最短路径   范围   code   

题目：

在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。

一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, ..., C_k 组成：

　　相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通（此时，C_i 和 C_{i+1} 不同且共享边或角）
　　C_1 位于 (0, 0)（即，值为 grid[0][0]）
　　C_k 位于 (N-1, N-1)（即，值为 grid[N-1][N-1]）
　　如果 C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）
　　返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径，返回 -1 。

示例：

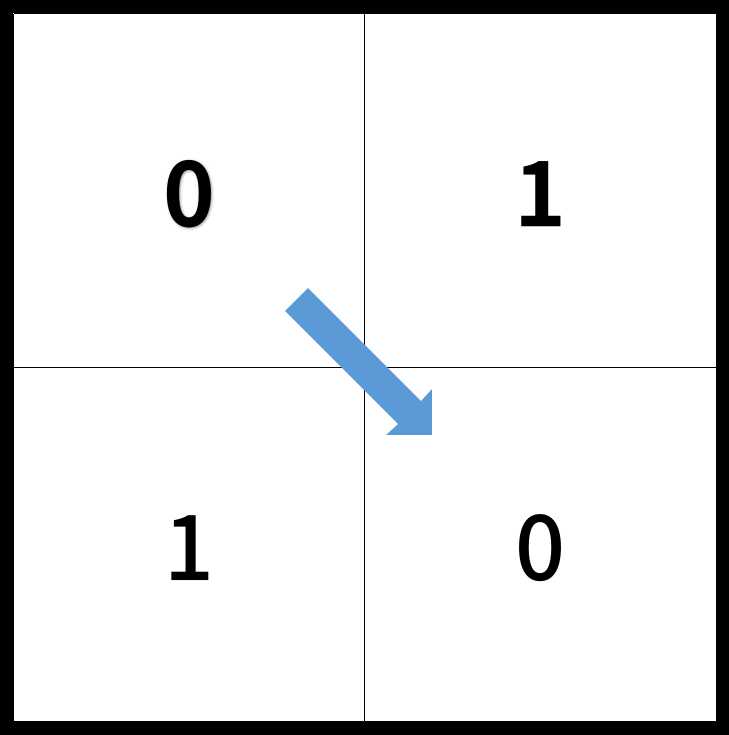
输入：[[0,1],[1,0]]                  输出：2

分析：

　　首先搞清楚，从左上角到右下角要想找出一条畅通的路径，途径的网格的值必须是0，而且题目中说相邻网格只要再八个方向之一连通那他们之间就是相通的，八个方向包括上、下、左、右、左上、左下、右上、右下，相互之间的距离差都是1，所以对于坐标为i，j的网格，其走向下一步可以考虑的选择有八个，需要对这八个选择做一些合法性判断和条件判断。

　　题目要求的是最短的畅通路径的长度，就是求路径长度的最优解，那么我们就可以利用广度优先遍历的方法去求最短路径，BFS是一层一层地进行遍历，每一层都是以上一层的点作为起点，每一层的点到起始点的距离都是相同的，而且每一层的点到各自父结点的距离也都相同，即为1。一个点遍历之后也不能再次访问。

　　那么我们利用BFS搜索算法的特点，因为BFS是一层一层的遍历，每一层的点与起始点的距离都是相同的，所以每一层的点都是最短路径的候选点，那么我们可以将与起始点具有相同距离的点认为是同一层的点，最终的结果是从每一层的候选点中各选出一个点，它们彼此连通，其距离最小，那就是最小路径。

　　所以我们从起始点开始，将起始点作为第一层，进行广度搜索，搜索的范围是当前层的每个网格点的八个方向上相邻的点，能够入选下一层候选点条件是这八个方向的相邻点的值要都为0，然后它们要在合法的范围内，如若满足这两个条件，那么就符合作为的下一层候选的网格点，同时将这些入选的下一层候选点的值设置为其与起始点的距离标识它属于哪一层，也将其标记为其已被访问，那么最终最先到达（n-1，n-1）这个点时的距离值就是最短距离，此时这个网格点拥有的值也即最短路径值。为啥后到右下角那个点的就不是最短路径呢，因为本题中，每次遍历只移动一个单位的距离，无论朝着哪个方向走都是一个单位的距离，后到的肯定是中间夺走了一些路程，距离肯定大于先到的距离。

　　在搜索的过程中，借助了队列，用于存储每一轮遍历得到的符合条件的网格点，而标记原本畅通的点已被访问过是通过赋予其与起始点的距离实现的。

代码：

    private int n;
    public int shortestPathBinaryMatrix(int[][] grid) {

        if (grid.length == 1 && grid[0][0] != 1){
            return 1;
        }else if (grid[0][0] == 1){
            return -1;
        }
        n = grid.length;
        int[][] dir = new int[][]{{1,0},{0,1},{1,1},{0,-1},{-1,0},{-1,1},{1,-1},{-1,-1}};
        LinkedList<int[]> queue = new LinkedList<>();

        queue.push(new int[]{0,0});
        grid[0][0] = 1;
        int count = 0;
        while (!queue.isEmpty()){

            int[] point = queue.poll();
            int i = point[0];
            int j = point[1];
            count = grid[i][j];

            for (int k = 0; k < 8; k++) {

                int c = i + dir[k][0];
                int r = j + dir[k][1];

                if (isRight(c,r) && grid[c][r] == 0){
                    queue.offer(new int[]{c,r});
                    grid[c][r] = count + 1;
                }
                if (c == n-1 && r == n-1 && grid[c][r] != 0){
                    return grid[c][r];
                }
            }

        }

        return -1;

    }

    public boolean isRight(int i,int j){

        return i >=0 && i < n && j >=0 && j < n;
    }

二进制矩阵中的最短路径（力扣第1091题）

标签：合作   binary   阻塞   选择   组成   ret   最短路径   范围   code   

原文地址：https://www.cnblogs.com/yxym2016/p/13138240.html