标签:lazy 重要 左右子树 loading 巩固 lin 节点 lse 不同
为什么会学替罪羊树?因为觉得AVL树那些的左旋右旋什么的太晕了啊QAQ
所以就在RHL大佬的推荐下,学习起了替罪羊树,这种不用旋转操作就能维护平衡的树
在OI界一直都会有这样的一句话:“暴力即优雅”,而诸如分块、替罪羊树则是对这句话的最好诠释
对于二叉搜索树,最重要的就是维护树的平衡,将时间复杂度保持在O(logN)左右,使其不会退化成一条链,从而到时时间复杂度增长到O(N)
像AVL树、Splay一类的树都是通过旋转来维持平衡,而替罪羊树呢,则是简单粗暴的“不平衡?那就拍扁重建!”
什么意思?让我们通过一些问答来理解一下
在每次插入点后,判断当前子树是否平衡,如果不平衡则拍扁重建
如果一棵树的左子树/右子树的存在的节点数量 > 这棵树的存在的节点数量× alpha,那么就要拍扁重建
alpha是我们人为选择的一个平衡因子,在0.5-1之间,一般选择0.7或0.8
在了解了替罪羊树的基础知识以后,让我们来学习一下替罪羊树的基本操作
intn,x,op,mep,tep,root,tmp[2000005],mem[2000005];
//tmp拍扁的时候用的内存空间
//mep指向内存池mem[]的指针
//tep指向拍扁时用的tmp[]的指针
struct node {
int lc,rc,v,valid,total; //valid子树未被删除的点数,total子树总点数
bool pd; //是否被删除:1表示未被删除,0表示被删除
} a[2000005];
inline bool flag(int now) { //判断是否需要平衡一下
if((double)a[now].valid*alpha<=(double)max(a[a[now].lc].valid,a[a[now].rc].valid)) return true;
return false;
}
inline void build(int l,int r,int &now) { //建树&调整维护
int mid=(l+r)>>1;
now=tmp[mid]; //tmp里存的是编号:把中间的元素取出来,中间元素的编号为now
if(l==r) {
a[now].lc=a[now].rc=0; //新插入的节点都为叶子节点,进行初始化
a[now].total=a[now].valid=1;
return;
}
if(l<mid) build(l,mid-1,a[now].lc); //mid已经建完了,建左右子树
else a[now].lc=0; //l==mid,则没有左儿子,但此时r那个节点作为了mid节点的右儿子
build(mid+1,r,a[now].rc);
/* 因为mid总是(l+r)>>1向下取整,所以只需要判断l是小于mid还是等于mid,而ri永远大于mid */
a[now].total=a[a[now].lc].total+a[a[now].rc].total+1; //更新节点信息
a[now].valid=a[a[now].lc].valid+a[a[now].rc].valid+1;
}
我们来看一看替罪羊树是怎么拍扁需要重构的树的,如下草图:
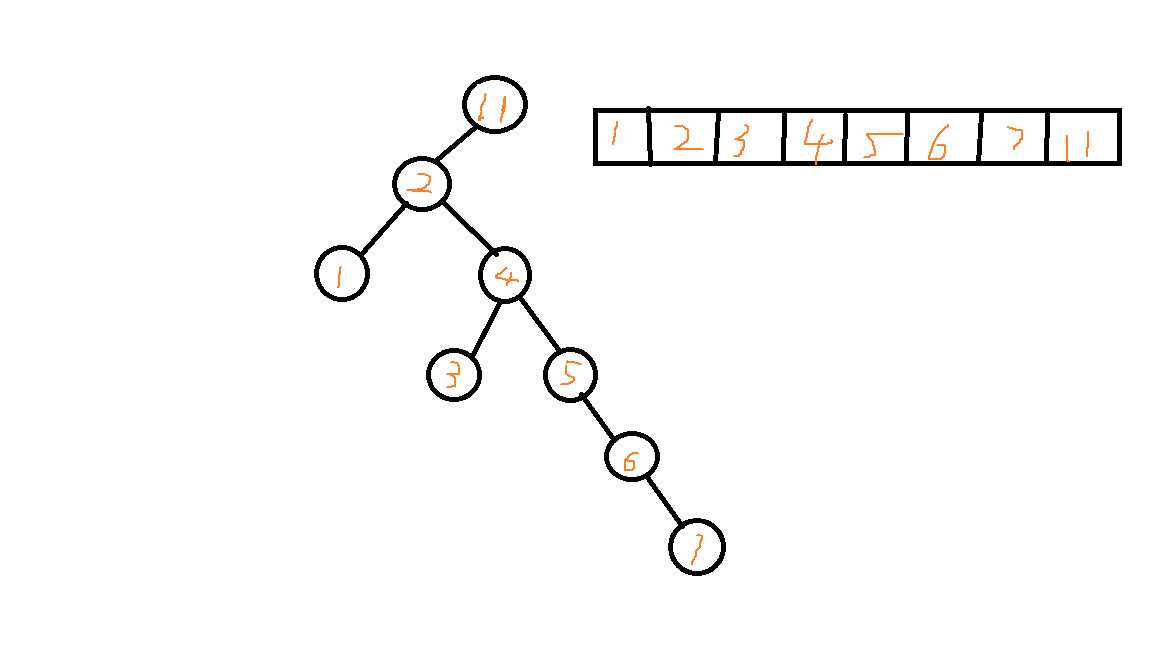
我们可以发现拍扁后的序列其实是已经排好序的,而这个顺序就是对这棵重建子树的中序遍历,所以我们重建前需要dfs一下
inline void dfs(int now) { //中序遍历(左根右),找出要被拍扁的节点的编号
if(!now) return; //叶子节点
dfs(a[now].lc);
if(a[now].pd==1) tmp[++tep]=now; //加入到拍扁的时候用的数组里存放(pd是惰性删除)
else mem[++mep]=now;
dfs(a[now].rc);
}
inline void rebuild(int &now) {
tep=0; //重建的子树要从头开始算
dfs(now); //dfs找到重建的顺序
if(tep) build(1,tep,now);
else now=0;
}
替罪羊树在插入时,是一边向下一边更新,这也是与其他树不同的地方
inline void insert(int &now,int k) {
if(!now) { //找到一个插入的位置
now=mem[mep--];
a[now].v=k;
a[now].pd=a[now].total=a[now].valid=1;
a[now].lc=a[now].rc=0;
return;
}
a[now].total++; //一边向下一边更新
a[now].valid++;
if(a[now].v>=k) insert(a[now].lc,k);
else insert(a[now].rc,k);
if(flag(now)==true) rebuild(now); //从下往上重建会更快(因为下面的子树小,好操作)
}
inline int findth(int k) { //查找值为k的排名
int now=root;
int ans=1;
while(now) {
if(a[now].v>=k) now=a[now].lc;
else {
ans+=a[a[now].lc].valid+a[now].pd; //+a[now].pd是因为相同大小的节点虽然放在一起,但是我不知道这个节点上相同的是不是还存在啊..所以得单独加该节点..至于valid是除现节点以外的子树大小。
now=a[now].rc;
}
}
return ans;
}
inline int findn(int k) { //查找排名为k的值
int now=root;
while(now) {
if(a[now].pd&&a[a[now].lc].valid+1==k) return a[now].v;
else if(a[a[now].lc].valid>=k) now=a[now].lc;
else {
k-=a[a[now].lc].valid+a[now].pd;
now=a[now].rc;
}
}
}
这里是通过转换为:先求值k的排名,再删除排名为k的数
注意一下,这里的删除都是惰性删除,即给删除的点打上标记
真正的删除是在DFS那里进行的
同时,删除之后我们也要判断一下是否需要重建(这里的判断条件与之前有略微不同)
inline void deleth(int &now, int k) { //删除排名为k的数
if(a[now].pd&&a[a[now].lc].valid+1==k) {
a[now].pd=0;
a[now].valid--;
return;
}
a[now].valid--;
if(a[a[now].lc].valid+a[now].pd>=k) deleth(a[now].lc,k);
else deleth(a[now].rc,k-a[a[now].lc].valid-a[now].pd);
}
inline void deletn(int k) { //删除值为k的数
deleth(root, findth(k));
if((double)a[root].total*alpha>a[root].valid) rebuild(root); //删太多也重建一下
}
现在来一发没有注释的Code
PS:以下给出的是例题1的代码(例题2的代码只需要在主程序上更改以下即可,文末会给出)
#include <bits/stdc++.h>
#define alp 0.8
using namespace std;
int n,x,op,mep,tep,root,tmp[2000005],mem[2000005];
struct node {
int lc,rc,v,valid,total;
bool pd;
} a[2000005];
inline bool flag(int now) {
if((double)a[now].valid*alp<=(double)max(a[a[now].lc].valid,a[a[now].rc].valid)) return true;
return false;
}
inline void build(int l,int r,int &now) {
int mid=(l+r)>>1;
now=tmp[mid];
if(l==r) {
a[now].lc=a[now].rc=0;
a[now].valid=a[now].total=1;
return ;
}
if(l<mid) build(l,mid-1,a[now].lc);
else a[now].lc=0;
build(mid+1,r,a[now].rc);
a[now].total=a[a[now].lc].total+a[a[now].rc].total+1;
a[now].valid=a[a[now].lc].valid+a[a[now].rc].valid+1;
}
inline void dfs(int now) {
if(!now) return ;
dfs(a[now].lc);
if(a[now].pd==1) tmp[++tep]=now;
else mem[++mep]=now;
dfs(a[now].rc);
}
inline void rebuild(int &now) {
tep=0;
dfs(now);
if(tep) build(1,tep,now);
else now=0;
}
inline void insert(int &now,int k) {
if(!now) {
now=mem[mep--];
a[now].v=k;
a[now].lc=a[now].rc=0;
a[now].pd=a[now].valid=a[now].total=1;
return ;
}
a[now].total++;
a[now].valid++;
if(a[now].v>=k) insert(a[now].lc,k);
else insert(a[now].rc,k);
if(flag(now)==true) rebuild(now);
}
inline int findth(int k) {
int now=root;
int ans=1;
while(now) {
if(a[now].v>=k) now=a[now].lc;
else {
ans+=a[a[now].lc].valid+a[now].pd;
now=a[now].rc;
}
}
return ans;
}
inline int findn(int k) {
int now=root;
while(now) {
if(a[now].pd&&a[a[now].lc].valid+1==k) return a[now].v;
else if(a[a[now].lc].valid>=k) now=a[now].lc;
else {
k-=a[now].pd+a[a[now].lc].valid;
now=a[now].rc;
}
}
}
inline void deleth(int &now,int k) {
if(a[now].pd&&a[a[now].lc].valid+1==k) {
a[now].pd=0;
a[now].valid--;
return ;
}
a[now].valid--;
if(a[a[now].lc].valid+a[now].pd>=k) deleth(a[now].lc,k);
else deleth(a[now].rc,k-a[a[now].lc].valid-a[now].pd);
}
inline void deletn(int k) {
deleth(root,findth(k));
if((double)a[root].total*alp>a[root].valid) rebuild(root);
}
int main() {
for(register int i=2000000;i>=1;i--) mem[++mep]=i;
scanf("%d",&n);
for(register int i=1;i<=n;i++) {
scanf("%d%d",&op,&x);
if(op==1) insert(root,x);
if(op==2) deletn(x);
if(op==3) printf("%d\n",findth(x));
if(op==4) printf("%d\n",findn(x));
if(op==5) printf("%d\n",findn(findth(x)-1));
if(op==6) printf("%d\n",findn(findth(x+1)));
}
return 0;
}
int main() {
for(register int i=2000000;i>=1;i--) mem[++mep]=i;
n=read();
m=read();
for(register int i=1;i<=n;i++) {
x=read();
insert(root,x);
}
for(register int i=1;i<=m;i++) {
op=read();
x=read();
x^=last;
if(op==1) insert(root,x);
if(op==2) deletn(x);
if(op==3) {
ans^=findth(x);
last=findth(x);
}
if(op==4) {
ans^=findn(x);
last=findn(x);
}
if(op==5) {
ans^=findn(findth(x)-1);
last=findn(findth(x)-1);
}
if(op==6) {
ans^=findn(findth(x+1));
last=findn(findth(x+1));
}
}
printf("%d",ans);
return 0;
}
终于总结完了!替罪羊树也算是入门了吧?
嗯..不过还需要多做题巩固应用,AVL树和Splay也得找时间学习
那....那就继续加油叭qvq
最后,如果有任何问题,欢迎指出,我们一起进步
标签:lazy 重要 左右子树 loading 巩固 lin 节点 lse 不同
原文地址:https://www.cnblogs.com/Eleven-Qian-Shan/p/13143290.html