标签:des 官方文档 频繁 适合 迭代 排列 抽取 desc 摘要
作者|Renu Khandelwal
编译|VK
来源|Medium
梯度下降法是一种减少成本函数的迭代机器学习优化算法,使我们的模型能够做出准确的预测。
成本函数(C)或损失函数度量模型的实际输出和预测输出之间的差异。成本函数是一个凸函数。
在神经网络中,我们的目标是训练模型具有最优的权值(w)来进行更好的预测。
我们用梯度下降法得到最优权值。
这可以用一个经典的登山问题来最好地解释。

在登山问题中,我们想要到达一座山的最低点,而我们的能见度为零。
我们不知道我们是在山顶上,还是在山的中间,还是非常接近底部。
我们最好的选择是检查我们附近的地形,并确定我们需要从哪里下降到底部。我们需要迭代地做这件事,直到没有更多的下降空间,也就是我们到达底部的时候。
我们将在稍后的文章中讨论,如果我们觉得已经到达了底部(局部最小值点),但是还有另一个山的最低点(全局最小值点),我们可以做什么。
梯度下降法帮助我们从数学上解决了同样的问题。
我们将一个神经网络的所有权值随机初始化为一个接近于0但不是0的值。
我们计算梯度,?c/?ω,它是成本相对于权重的偏导数。
α是学习率,有助于对梯度下降法调整权重
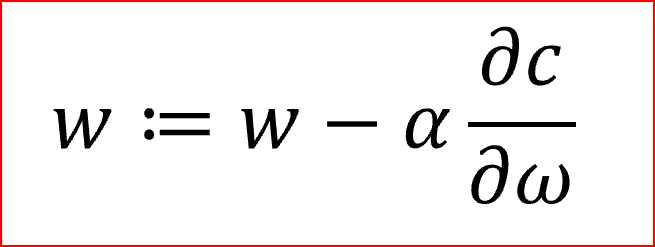
我们需要同时更新所有神经元的权重
学习率控制着我们应该在多大程度上根据损失梯度调整权重。学习速率是随机初始化的。
值越低,学习速度越慢,收敛到全局最小。
较高的学习率值不会使梯度下降收敛
由于我们的目标是最小化成本函数以找到最优的权值,所以我们使用不同的权值运行多个迭代,并计算成本以获得最小的成本,如下所示
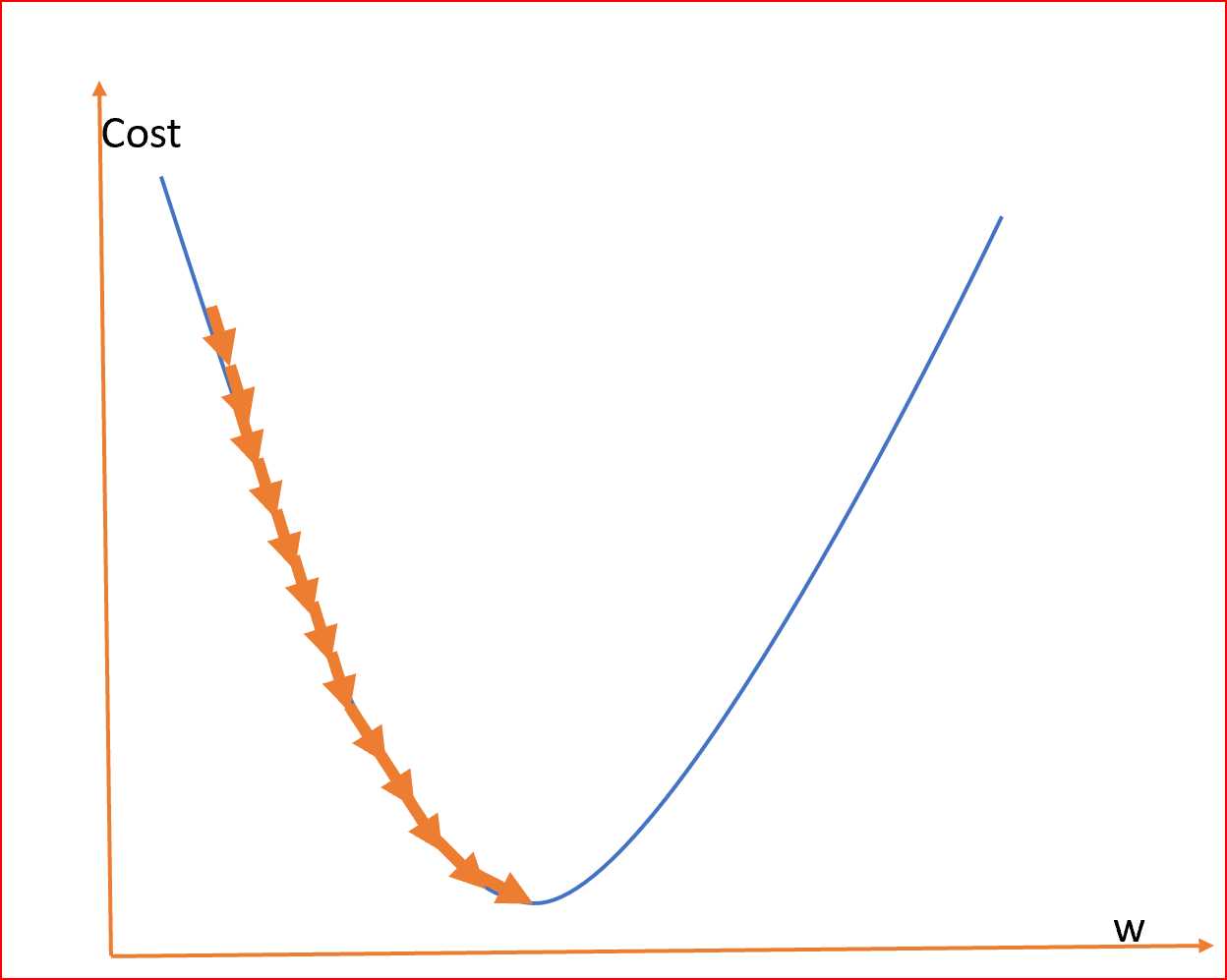
这座山可能有两个不同的底部,用同样的方法,我们也可以得到成本和权重之间的局部和全局最小点。
全局最小是整个域的最小点,局部最小是一个次优点,在这里我们得到一个相对最小的点,但不是如下所示的全局最小点。
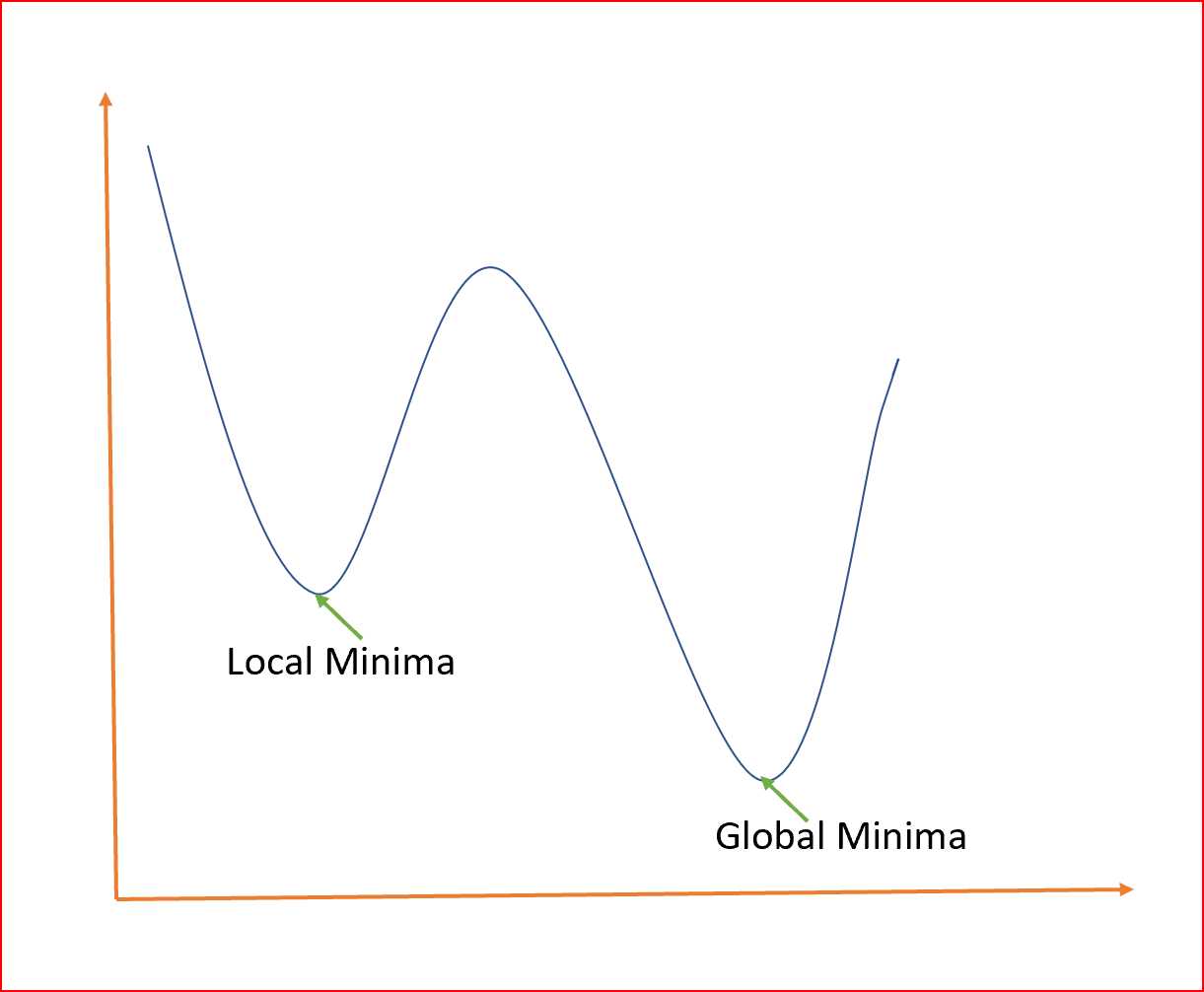
我们如何避免局部最小值,并始终尝试得到基于全局最小值的最优权值?
首先我们来了解一下梯度下降的不同类型
不同类型的梯度下降是
在批量梯度中,我们使用整个数据集来计算梯度下降每次迭代的代价函数的梯度,然后更新权值。
由于我们使用整个数据集来计算梯度收敛速度较慢。
如果数据集很大,包含数百万或数十亿个数据点,那么它就需要大内存和并且是计算密集的。
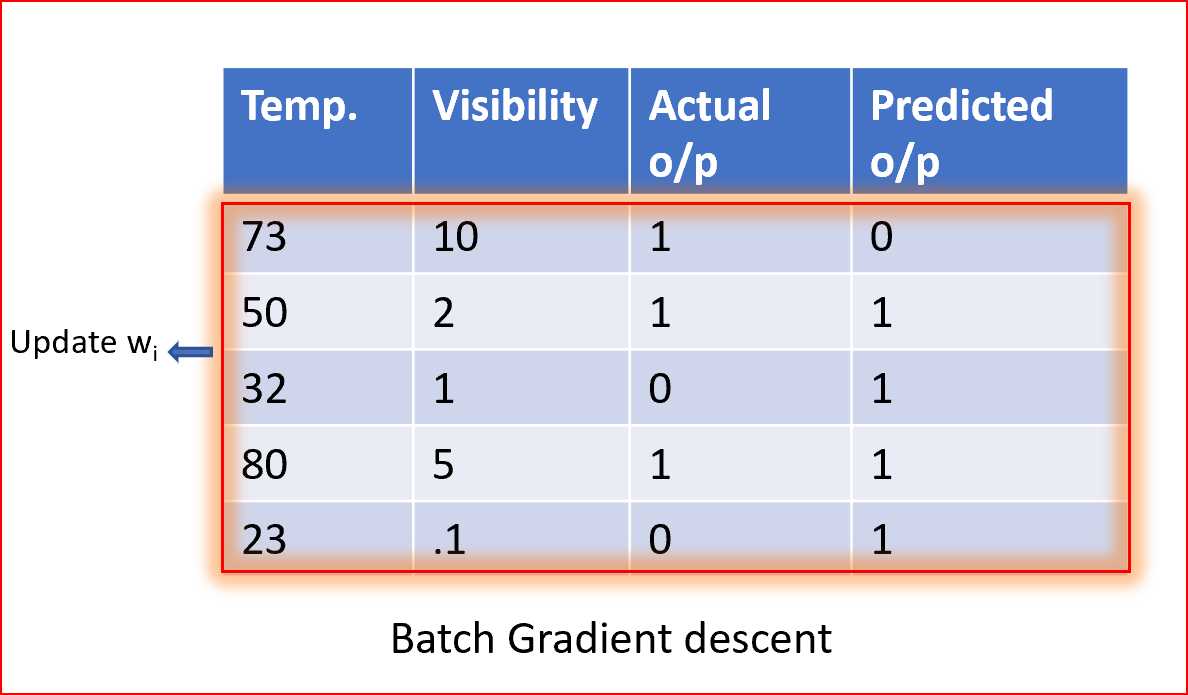
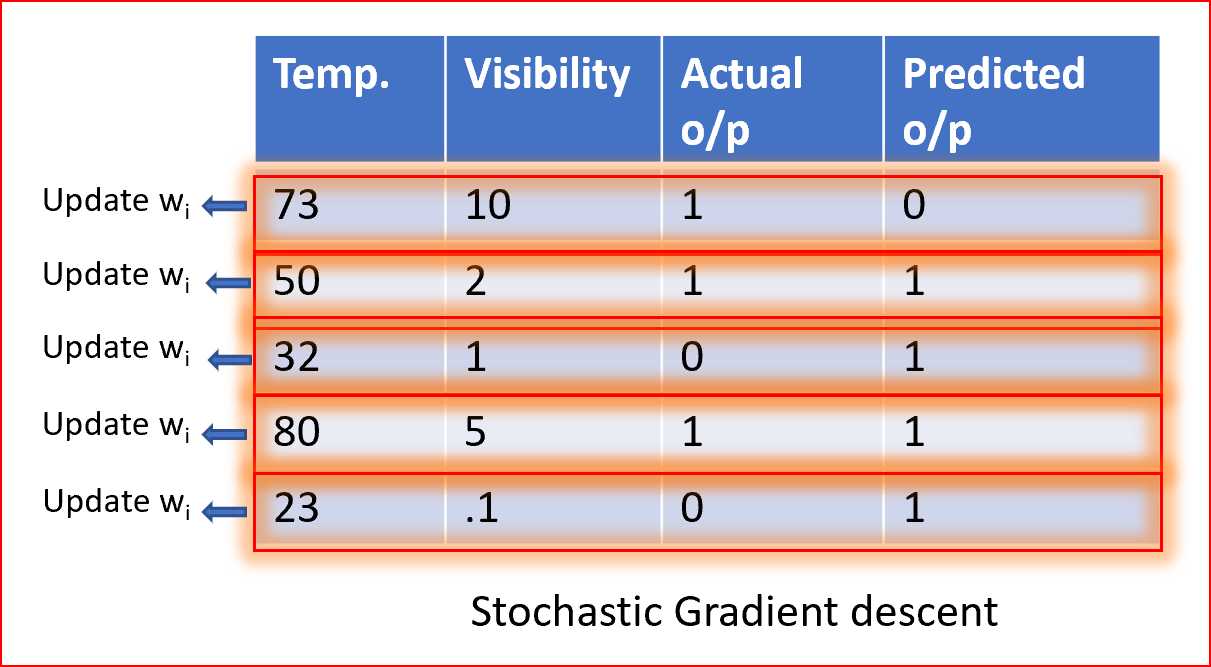
在随机梯度下降法中,我们使用单个数据点或实例来计算梯度,并在每次迭代中更新权值。
我们首先需要将数据集的样本随机排列,这样我们就得到了一个完全随机的数据集。由于数据集是随机的,并且每个示例的权值都是可以更新的,所以权值和代价函数的更新将是到处乱跳的,如下所示
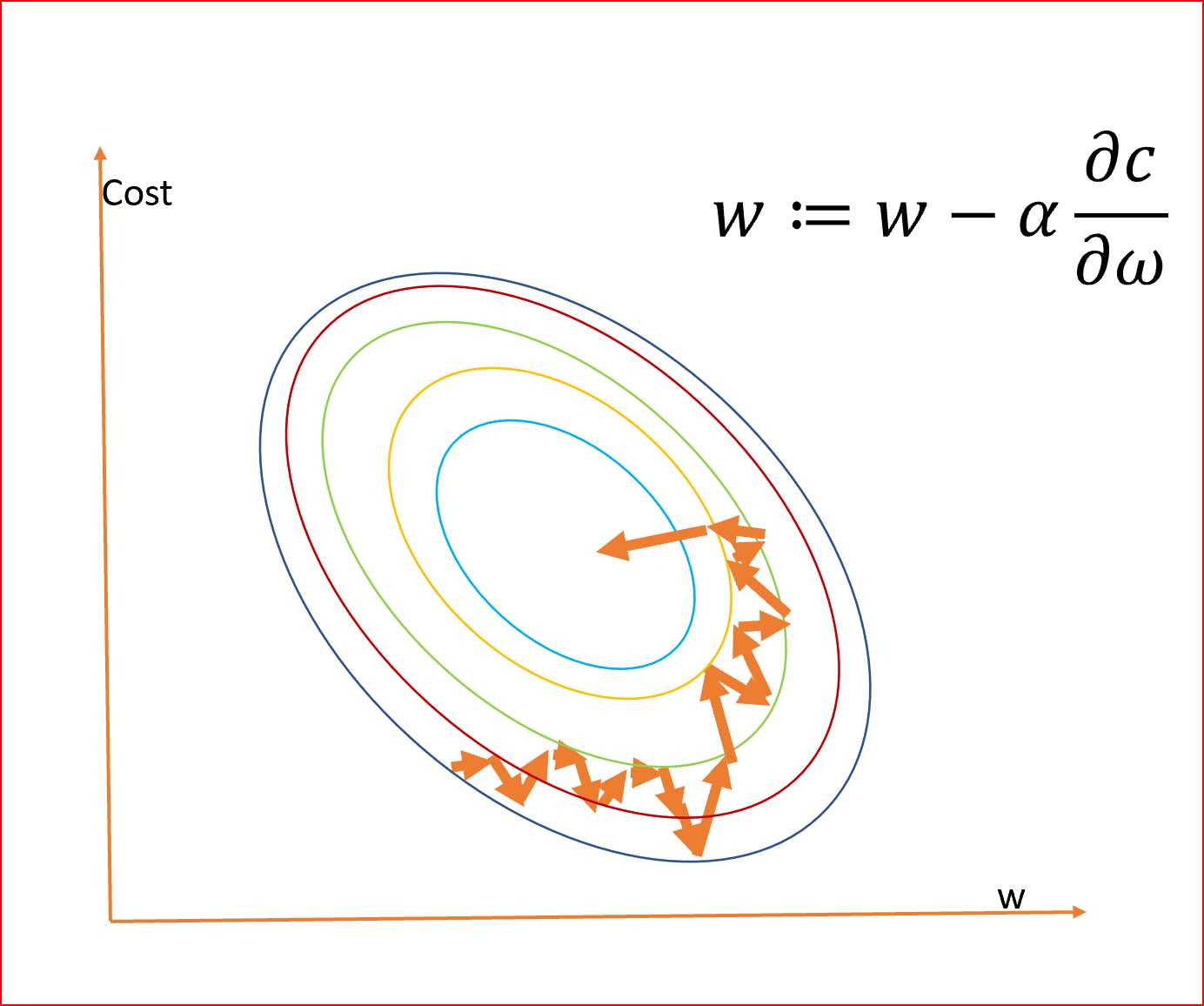
随机样本有助于得到全局的最小值,避免陷入局部的最小值。
对于非常大的数据集,学习要快得多,收敛也快得多。
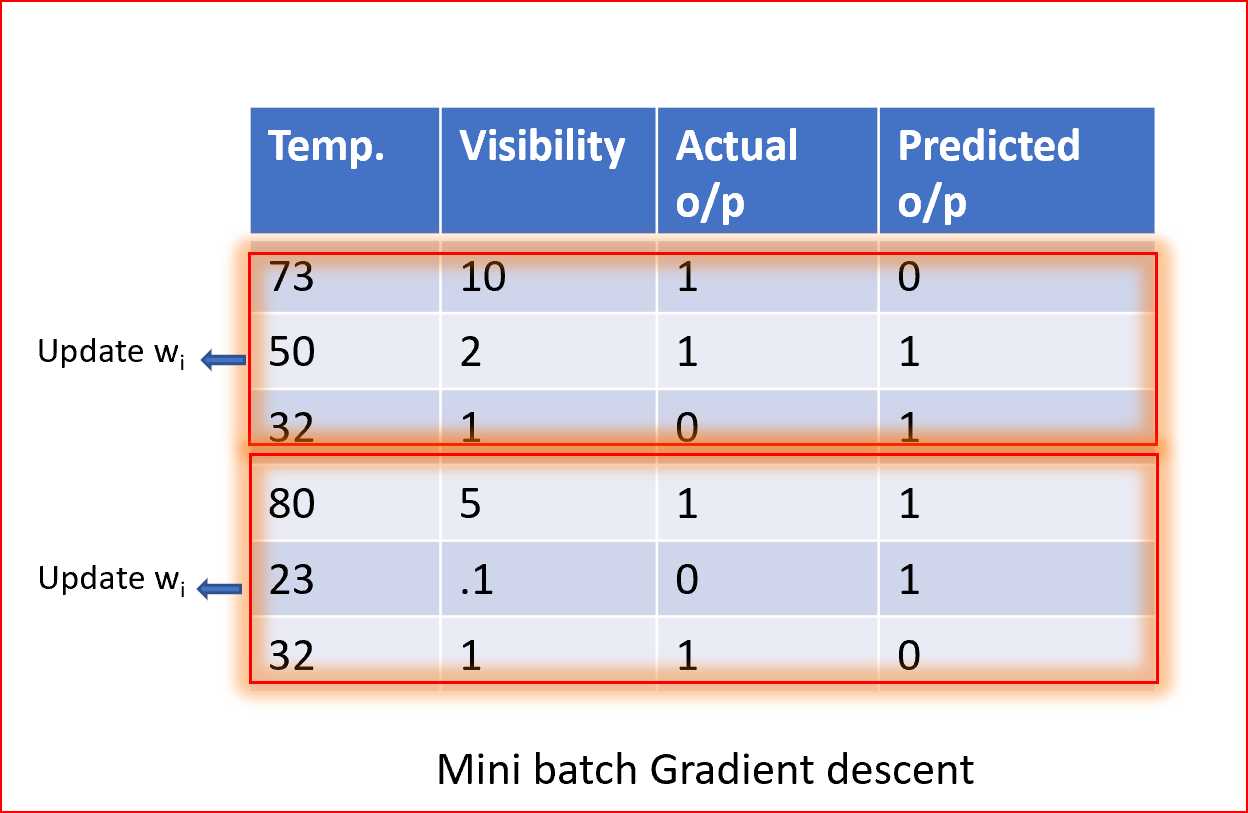
摘要小批量梯度法是一种随机梯度下降法,它不采用单一训练样本,而是采用小批量样本。
小批量梯度下降法应用广泛,收敛速度快,稳定性好。
批处理大小可以根据数据集的不同而有所不同。
当我们取一批不同的样本时,它减少了权值更新的方差噪声,有助于更快地获得更稳定的收敛。
原文链接:https://medium.com/@arshren/gradient-descent-5a13f385d403
欢迎关注磐创AI博客站:
http://panchuang.net/
sklearn机器学习中文官方文档:
http://sklearn123.com/
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/
标签:des 官方文档 频繁 适合 迭代 排列 抽取 desc 摘要
原文地址:https://www.cnblogs.com/panchuangai/p/13154160.html