标签:www 二进制 加密算法 函数 实现 排列 计算 扩展欧几里得 ima
RSA的整体逻辑就是将一个数在经过一次运算后能变回原数,这个运算就是求幂然后取模,将这个运算拆成两个部分,其中一部分作为公钥给用户,另一部分作为私钥储存在服务器,用户用公钥运算后发送给服务器,然后服务器再用私钥运算,最终能得到还原后的数据,这就是RSA的算法流程
算法原理解释
所有涉及的知识(均只写出需要使用的部分)
互质关系
中国剩余定理
欧拉φ函数 费马-欧拉定理(数论)
最大公因子
扩展欧几里得算法
互质关系
涉及的结论 1. 任意两个质数构成互质关系,比如13和61 2. 一个数是质数,另一个数只要不是前者的倍数,两者就构成互质关系,比如3和10 3. 如果两个数之中,较大的那个数是质数,则两者构成互质关系,比如97和57 4. 1和任意一个自然数是都是互质关系,比如1和99 5. p是大于1的整数,则p和p-1构成互质关系,比如57和56 6. p是大于1的奇数,则p和p-2构成互质关系,比如17和15
中国剩余定理
取两个质数n、m,则对于任意正整数x < n * m,均有唯一的(a,b)数对使得a = x mod n、b = x mod m
例:
取n = 3,m = 5,则n * m = 15
x a b
14 2 4
13 1 3
12 0 2
11 2 1
10 1 0
9 0 4
8 2 3
7 1 2
6 0 1
5 2 0
4 1 4
3 0 3
2 2 2
1 1 1
其中a有n - 1个不为0的值,b有m - 1个不为0的值
欧拉φ函数
对正整数n,欧拉函数φ(n)是小于或等于n的正整数中与n互质的数的数目
因为需要将比n小且不互质的整数去除掉,则根据容斥定理,可以得到
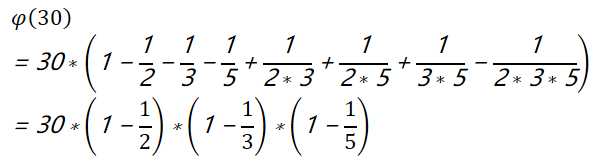
即φ函数公式为:
当n=p*q,其中p和q均为质数时,乘积性质证明:
方法一:
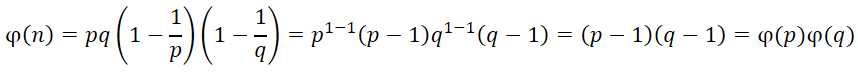 ①
①
证毕
方法二:
根据中国剩余定理,x与(a,b)数对一一对应,则:
当a、b均不为0时,(a,b)所对应的x与n * m互质,因为n、m均为质数,则φ(n)= n - 1,φ(m)= m - 1
根据排列组合,(a,b)数对的数量为φ(n)*φ(m),也等于φ(n * m)的数量,即φ(n * m)=φ(n)* φ(m)
证毕
例:
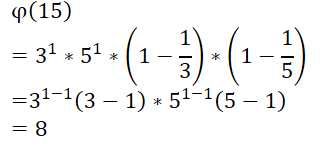
与中国剩余定理中的红色行数量一致,并且通过剩余定理,可以有另一种思路推出φ函数公式,参考文末链接
欧拉定理
若a与n互质,则
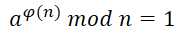 ②
②模反元素
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1,即
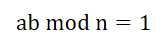 ③
③
证明:
因为a与n互质,则由②得
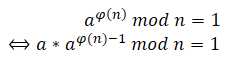
即一定存在b,使得a与b为模反元素
扩展欧几里得算法
在③中,RSA算法一般将质数a取为65537,二进制表示为10000000000000001,因为绝大部分位置是0,因此简化了加密时的运算量
在1024位加密下,质数p和q随机取为512位二进制数,使得n为1024位,然后根据a和n,求得a的模反元素b
但是在实际计算过程中,如此大的幂运算,是几乎不可能直接计算出来的,因此使用了扩展欧几里得算法来计算
RSA算法
下面展示1024位加密算法的步骤
第一步:
随机取两个512位二进制长度的质数p和q,表示成十进制,以便后续运算
第二步:
计算p和q的乘积n,然后由①可得φ(n)=(p-1)(q-1)
第三步:
根据③,将a、b分别记为e、d,意为encode和decode,其中e常设为65537,也可使用其他质数,然后根据④求得d
第四步:
将e和n封装为公钥,d和n封装为私钥,将公钥发送给用户,然后将私钥保存在服务器端
使用方法:
用户使用公钥加密后传输给服务器,服务器使用储存的私钥解密即完成整个RSA加密流程
感谢
算法导论 null RSA算法原理(一) http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html
ACM数论之旅7---欧拉函数的证明及代码实现(我会证明都是骗人的╮( ̄▽ ̄)╭)
https://www.cnblogs.com/linyujun/p/5194170.html
标签:www 二进制 加密算法 函数 实现 排列 计算 扩展欧几里得 ima
原文地址:https://www.cnblogs.com/Pyrokine/p/13072526.html