标签:width size loading 个数 代码 gis span lazy 公式
对于一般的指数曲线如:y=a*e^(k*t),可以先对两边求对数得到:log(y) = log(a)+k*t 这样的曲线,然后用最小二乘来计算系数。
但是对于修正指数曲线如:y=k+a*b^t 这样的函数,没法直接求对数然后用最小二乘,因为有一个常数项k,这里可以利用三和法来计算系数。
对于曲线 y = k+a*b^t,三和法计算各系数公式如下:
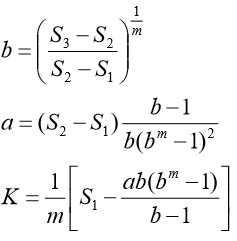
其中:
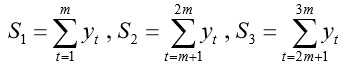
其中:
m=n/3,这里的n就是所有数据的总个数。
这种方法不止可以计算形如y = k+a*b^t这样的修正指数曲线,还可以计算形如y=k*a^(b^t)这样的compertz曲线和形如y=1/(k+a*b^t)这样的logistic曲线,因为compertz曲线可以通过求log得到修正指数曲线,而logistic曲线可以通过求倒数得到修正指数曲线。
matlab代码如下:
clear all; close all; clc; a=45.73423; b=0.4234; k=34.34534; t=1:30; %t为整数没问题 t=1:0.1:30; %t为小数有问题,只能求出k y=k+a*b.^t; plot(t,y); m=floor(length(t)/3); S1 = sum(y(1:m)); S2 = sum(y(m+1:2*m)); S3 = sum(y(2*m+1:3*m)); b = ((S3-S2)/(S2-S1))^(1.0/m); a = (S2-S1)*(b-1)/(b*(b^m-1)^2); k = (1.0/m)*(S1 - a*b*(b^m-1)/(b-1)); y1=k+a*b.^t; hold on; plot(t,y1,‘ro‘); newy = y - k; %log(newy) = log(a) + log(b)*t; X = [t‘ ones(length(t),1)]; Y = log(newy)‘; C = inv(X‘*X)*X‘*Y; a = exp(C(2)); b = exp(C(1)); y=k+a*b.^t; hold on; plot(t,y,‘r.‘);
对于上面的程序,有一点需要注意,当t为整数变化时,该方法求得的结果是正确的。
但是当t为小数变化是,该方法直接求得的a和b是错误的,但是k是正确的,有了k,同样可以利用最小二乘计算出a和b。
结果如下:
当t为整数时:
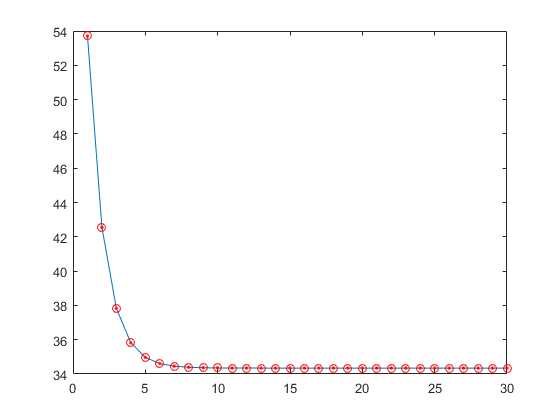
当t为小数时:
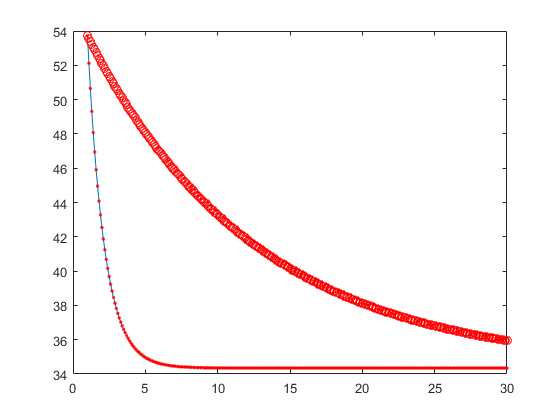
标签:width size loading 个数 代码 gis span lazy 公式
原文地址:https://www.cnblogs.com/tiandsp/p/13168643.html