Why Did the Cow Cross the Road I P 题解

标签：out   移动   space   new   getchar   def   i++   include   cas   

老早之前做的，补题解。

简化の题意

给两个长度为 \(n\) 的排列 \(A\),\(B\)，允许对任意一个排列进行一次旋转

定义为\(\begin{cases}A_i\gets A_{i-1}&i<n \\A_n\gets A_1\end{cases}\)

设四元组 \(\{i,j,k,l\} (i\leq k\leq n,j\leq l \leq n)\) 满足\(\begin{cases}A_i=B_j\\A_k=B_l\end{cases}\) 求四元组的最小数量 复杂erの题意。

思路

首先我们发现这两个排列可以表示成一个排列，以样例为例:

A:5 4 1 3 2
B:1 3 2 5 4

把 \(A \to B\) 的映射关系建立一下（所以其实有两种表示方法，这里暂时只考虑一种），就得到

4 5 1 2 3

明显的，满足题意的四元组的个数为这个排列的逆序对的个数。

接下来考虑旋转，上图：

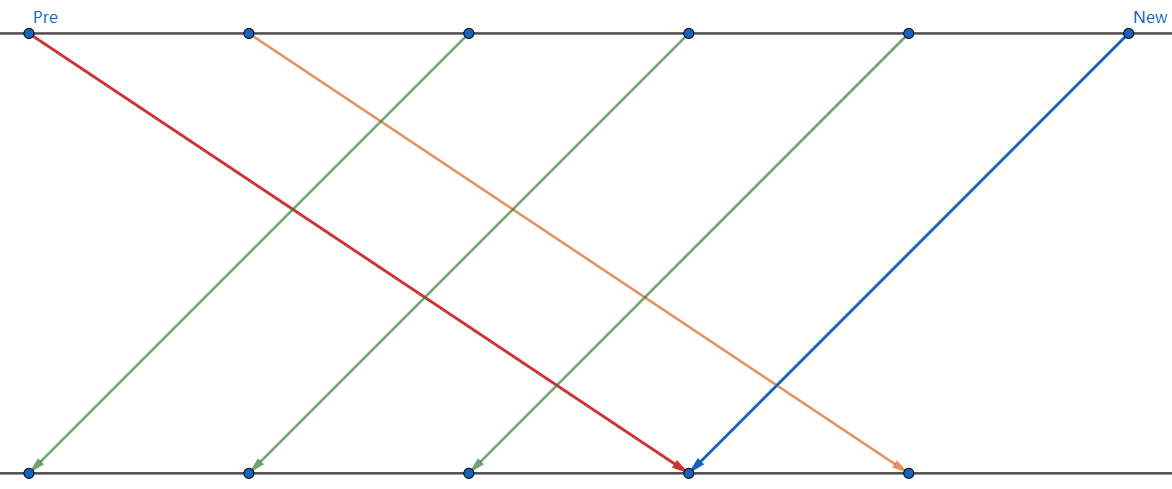
设当前Pre点移动到New点，所以我们要销毁红色边，新建蓝色边。从图中可以看出，绿色的边将不再与红色的边交叉，而橙色的边将与新的蓝色边交叉，所以旋转后的的答案将减2。也即减去第二排左边的点再加上右边的点。

注意到第二排的点不会改变位置，所以每一次旋转并不会影响其他旋转的答案，所以，对于每一次旋转，我们都可以 \(O(1)\) 求出旋转后的答案。

一个重要的地方：两排的旋转并不等价，所以要分别对两边求两次解。

代码

#include<cstdio>
#include<iostream>
#define lowb(x)(x&-x)
using namespace std;
int n,a[100010],b[100010],c[100010],t[100010];
long long ans=0x7fffffffffffffff,sum;
void read(int &x){
	char c=getchar();
	for(;c<33;c=getchar());
	for(x=0;(47<c)&&(c<58);x=x*10+c-48,c=getchar());
}
void sg(int x,int c){
	for(;x<=n;x+=lowb(x)){
		t[x]+=c;
	}
}
int call(int x){
	int re=0;
	for(;x;x-=lowb(x)){
		re+=t[x];
	}
	return(re);
}
void solve(int *a,int *b){
	for(int i=1;i<=n;i++){
		c[b[i]]=i;
		t[i]=0;
	}
	sum=0;
	for(int i=1;i<=n;i++){
		sum+=call(n-c[a[i]]+1);
		sg(n-c[a[i]]+1,1);
	}
	for(int i=1;i<=n;i++){
		sum-=c[a[i]]-1;
		sum+=n-c[a[i]];
		ans=min(ans,sum);
	}
}
int main(){
	freopen("mincross.in","r",stdin);
	freopen("mincross.out","w",stdout);
	read(n);
	for(int i=1;i<=n;i++){
		read(a[i]);
	}
	for(int i=1;i<=n;i++){
		read(b[i]);
	}
	solve(a,b);
	solve(b,a);
	printf("%lld",ans);
	fclose(stdin);
	fclose(stdout);
	return(0);
}

Why Did the Cow Cross the Road I P 题解

标签：out   移动   space   new   getchar   def   i++   include   cas   

原文地址：https://www.cnblogs.com/groundwater/p/13169459.html