码迷，mamicode.com
首页 > 其他好文 > 详细

数据结构上机实验(3)

时间：2020-06-20 23:57:15      阅读：80      评论：0      收藏：0      [点我收藏+]

标签：tar   end   必须   class   回溯   开始   n皇后问题   lazy   坐标   

1、实现顺序栈的各种基本运算算法

技术图片

#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>
#define Max_Size 100
typedef char ElemType;
typedef struct 
{
    ElemType data[Max_Size];
    int top;
}SeqStack;

//初始化栈
static void init_stack(SeqStack *&s) 
{
    s = (SeqStack *)malloc(sizeof(SeqStack));
    s->top = -1;
}
//销毁顺序栈
static void destroy_stack(SeqStack *&s)
{
    free(s);
}
//判断栈空否
static bool stack_empty(SeqStack *s)
{
    return (s->top == -1);
}
//进栈
static bool push(SeqStack *&s,ElemType e)
{
    if(s->top==(Max_Size-1))   //栈满的情况,栈上溢出
        return false;
    s->top++;
    s->data[s->top]=e;
    return true;
}
//出栈
static bool pop(SeqStack *&s,ElemType &e)
{
    if(s->top==-1)   //栈为空的情况,即栈下溢出
        return false;
    e=s->data[s->top];
    s->top--;
    return true;
}
//取栈顶元素
static bool get_top(SeqStack *s,ElemType &e)
{
    if(s->top==-1)
        return false;
    e=s->data[s->top];
    return true;
}

int main()
{
    ElemType e;
    SeqStack *s;

    printf("顺序栈s的基本运算如下:\n");
    printf("  (1)初始化栈s\n");
    init_stack(s);
    printf("  (2)栈为%s\n",(stack_empty(s) ? "空" : "非空"));
    printf("  (3)依次进栈元素a,b,c,d,e\n");
    push(s, ‘a‘);
    push(s, ‘b‘);
    push(s, ‘c‘);
    push(s, ‘d‘);
    push(s, ‘e‘);
    printf("  (4)栈为%s\n",(stack_empty(s) ? "空" : "非空"));
    printf("  (5)出栈序列:");
    while(!stack_empty(s))
    {
        pop(s, e);
        printf("%c ", e);
    }
    printf("\n");
    printf("  (6)栈为%s\n",(stack_empty(s) ? "空" : "非空"));
    printf("  (7)释放栈\n");
    destroy_stack(s);
}

技术图片

2、实现链栈的各种基本运算的算法

技术图片

#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>

typedef char ElemType;
typedef struct linknode
{
    ElemType data;
    struct linknode *next;
}LinkStNode;

//初始化链栈
static void init_stack(LinkStNode *&s) 
{
    s = (LinkStNode *)malloc(sizeof(LinkStNode));
    s->next = NULL;
}
//销毁链栈
static void destroy_stack(LinkStNode *&s)
{
    LinkStNode *p = s->next;
    while(p != NULL)
    {
        free(s);
        s = p;
        p = p->next;
    }
    free(s);   //s指向尾结点,释放其空间
}
//判断链栈空否
static bool stack_empty(LinkStNode *s)
{
    return (s->next == NULL);
}
//进栈
static void push(LinkStNode *&s,ElemType e)
{
    LinkStNode *p;
    p=(LinkStNode *)malloc(sizeof(LinkStNode));
    p->data=e;
    p->next=s->next;
    s->next=p;
}
//出栈
static bool pop(LinkStNode *&s,ElemType &e)
{
    LinkStNode *p;
    if(s->next==NULL)
        return false;
    p=s->next;
    e=p->data;
    s->next=p->next;   //删除首节点
    free(p);
    return true;
}
//取栈顶元素
static bool get_top(LinkStNode *s, ElemType &e)
{
    if(s->next==NULL)
        return false;
    e=s->next->data;   //提取首节点值
    return true;
}

int main()
{
    ElemType e;
    LinkStNode *s;

    printf("链栈s的基本运算如下:\n");
    printf("   (1)初始化栈s\n");
    init_stack(s);
    printf("   (2)栈为%s\n", (stack_empty(s) ? "空" : "非空"));
    printf("   (3)依次进栈元素a,b,c,d,e\n");
    push(s, ‘a‘);
    push(s, ‘b‘);
    push(s, ‘c‘);
    push(s, ‘d‘);
    push(s, ‘e‘);
    printf("   (4)栈为%s\n", (stack_empty(s) ? "空" : "非空"));
    printf("   (5)出栈序列:");
    while(!stack_empty(s))
    {
        pop(s, e);
        printf("%c ", e);
    }
    printf("\n");
    printf("   (6)栈为%s\n", (stack_empty(s) ? "空" : "非空"));
    printf("   (7)释放栈\n");
    destroy_stack(s);
}

技术图片

3、实现环形队列各种基本运算算法

技术图片

#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>
#define MAX_SIZE 100

typedef char ElemType;
typedef struct
{
    ElemType data[MAX_SIZE];
    int queue_front;   //队首指针
    int queue_rear;    //队尾指针
}SeqQueue; 


//初始化队列
static void init_queue(SeqQueue *&q) 
{
    q = (SeqQueue *)malloc(sizeof(SeqQueue)); // 动态分配存储空间
    q->queue_front = q->queue_rear = 0;   //空
}
//销毁队列q
static void destroy_queue(SeqQueue *&q)
{
    free(q);
}
//判断队列q是否空
static bool queue_empty(SeqQueue *q)
{
    return (q->queue_front == q->queue_rear);
}
//入队
static bool en_queue(SeqQueue *&q, ElemType e)
{
    if((q->queue_rear + 1) % MAX_SIZE == q->queue_front)   //队满,上溢出,返回假
        return false;
    q->queue_rear = (q->queue_rear + 1) % MAX_SIZE;   //计算队尾指针
    q->data[q->queue_rear] = e;   //将元素e入队
    return true;
}
//出队
static bool de_queue(SeqQueue *&q, ElemType &e)
{
    if(q->queue_front == q->queue_rear)   //队空,下溢出,返回假
        return false;
    q->queue_front = (q->queue_front + 1) % MAX_SIZE;   //计算队首指针
    e = q->data[q->queue_front];   //提取队列中的元素
    return true;
}

int main()
{
    ElemType e;
    SeqQueue *q;

    printf("环形队列基本运算如下:\n");
    printf("   (1)初始化队列q\n");
    init_queue(q);
    printf("   (2)依次进队元素a、b、c\n");
    if(!en_queue(q, ‘a‘))
        printf("\t提示:队满,不能入队\n");
    if(!en_queue(q, ‘b‘))
        printf("\t提示:队满,不能入队\n");
    if(!en_queue(q, ‘c‘))
        printf("\t提示:队满,不能入队\n");
    printf("   (3)队列为%s\n", (queue_empty(q) ? "空" : "非空"));
    if(!de_queue(q, e))
        printf("队空,不能出队\n");
    else
        printf("   (4)出队一个元素%c\n", e);

    printf("   (5)依次进队元素d、e、f\n");
    if(!en_queue(q, ‘d‘))
        printf("\t提示:队满,不能入队\n");
    if(!en_queue(q, ‘e‘))
        printf("\t提示:队满,不能入队\n");
    if(!en_queue(q, ‘f‘))
        printf("\t提示:队满,不能入队\n");

    printf("   (6)出队列序列: ");
    while(!queue_empty(q))
    {
        de_queue(q, e);
        printf("%c ", e);
    }
    printf("\n");
    printf("   (7)释放队列\n");
    destroy_queue(q);
}

技术图片

4、实现链队的各种基本运算的算法

技术图片

#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>
#define MAX_SIZE 100

typedef char ElemType;
typedef struct DataNode
{
    ElemType data;
    struct DataNode *next;
}DataNode; 
typedef struct
{
    DataNode *queue_front;   //队头指针
    DataNode *queue_rear;   //队尾指针
}LinkQuNode; 


//初始化队列
static void init_queue(LinkQuNode *&q)
{
    q = (LinkQuNode *)malloc(sizeof(LinkQuNode)); 
    q->queue_front = q->queue_rear = NULL;
}
//销毁队列q
static void destroy_queue(LinkQuNode *&q)
{
    DataNode *p = q->queue_front;   //p指向队头数据结点
    DataNode *r;

    if(p != NULL)
    {
        r = p->next;   //r指向队列中第一个数据结点
        while(r != NULL)
        {
            free(p);
            //p,r同步后移一个结点
            p = r;
            r = p->next;
        }
    }
    free(p);
    free(q);
}
//判断队列q是否空
static bool queue_empty(LinkQuNode *q)
{
    return (q->queue_rear == NULL);
}
//入队
static void en_queue(LinkQuNode *&q, ElemType e)
{
    DataNode *p;   //创建新结点p
    p = (DataNode *)malloc(sizeof(DataNode)); 
    p->data = e;
    p->next = NULL;
    // 若链队为空,则新结点既是队首结点又是队尾结点
    if(q->queue_rear == NULL)
        q->queue_front = q->queue_rear = p;
    else
    {
        //将新结点p链到队尾,并将queue_rear指向它
        q->queue_rear->next = p;
        q->queue_rear = p;
    }
}
//出队
static bool de_queue(LinkQuNode *&q, ElemType &e) 
{
    DataNode *t;
    if(q->queue_rear == NULL)   //队列为空
        return false;
    t = q->queue_front;   //t指向第一个数据结点
    if(q->queue_front == q->queue_rear)   //队列中只有一个结点时
    {
        q->queue_front = q->queue_rear = NULL;
    }
    else   //队列中有多个结点时
    {
        q->queue_front = q->queue_front->next;   //队首指针后移一个结点
    }
    e = t->data;   //从t结点中提取数据元素
    free(t); 
    return true;
}

int main()
{
    ElemType e;
    LinkQuNode *q;

    printf("链队的基本运算如下:\n");
    printf("  (1)初始化链队q\n");
    init_queue(q);
    printf("  (2)依次进链队元素a、b、c\n");
    en_queue(q, ‘a‘);
    en_queue(q, ‘b‘);
    en_queue(q, ‘c‘);
    printf("  (3)链队为%s\n", (queue_empty(q) ? "空" : "非空"));

    if(!de_queue(q, e))
        printf("\t提示:队空,不能出队\n");
    else
        printf("  (4)出队一个元素%c\n", e);
    printf("  (5)依次进链队元素d、e、f\n");
    en_queue(q, ‘d‘);
    en_queue(q, ‘e‘);
    en_queue(q, ‘f‘);
    printf("  (6)出链队序列: ");
    while(!queue_empty(q))
    {
        de_queue(q, e);
        printf("%c ", e);
    }
    printf("\n");
    printf("  (7)释放链队\n");
    destroy_queue(q);
}

技术图片

5、用栈求解迷宫问题的所有路径及最短路径程序

技术图片

技术图片

//本题书上代码有误，运行后为死循环输出不了所有路径
//本题代码学习于CSDN作者- 不想悲伤到天明
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std ;
const int MAX = 105 ;
int mg[MAX][MAX] ={
{1,1,1,1,1,1},
{1,0,0,0,1,1},
{1,0,1,0,0,1},
{1,0,0,0,1,1},
{1,1,0,0,0,1},
{1,1,1,1,1,1}
 
};//迷宫地图
 
struct Point{
	int x ;// 路径横坐标
	int y ;// 路径纵坐标 ;
	int di ;// 方向
};
typedef struct{
	int top ;
	Point data[MAX] ;
}Stack;
class STACK{
	
	public:
		void InitStack(Stack *&s);
		bool StackEmpty(Stack *&s);
		bool Push(Stack *&s ,Point &e);
		bool Pop(Stack *&s ,Point &e);
		bool GetTop(Stack *&s ,Point &e);
};
void STACK::InitStack(Stack *&s)
{
	s = (Stack *)malloc(sizeof(Stack)) ;
	s->top = -1  ;
	return ;
}
bool STACK::StackEmpty(Stack *&s)
{
	return (s->top ==-1) ;
}
bool STACK::Push(Stack *&s ,Point &e)
{
	if(s->top == MAX -1)
	{
		return false ;
	}
	s->top++ ;
	s->data[s->top] = e ;
	return true ;
}
bool STACK::Pop(Stack *&s ,Point &e)
{
	if(s->top ==-1)
	{
		return false ;
	}
	e = s->data[s->top] ;
	s->top-- ;
	return true ;
	
}
bool STACK::GetTop(Stack *&s ,Point &e)
{
	if(s->top ==-1)
	{
		return false ;
	}
	e = s->data[s->top ] ;
	return true ;
}

int count = 1  ; // 记录路径数目
int minlen = 0x3f3f;   //最短路径长度，先设为最大 
Point path[MAX] ;
void dfs(Point start ,Point end)
{
	bool find ;
	Point head ;
	STACK a ;
	Stack *s ;
	a.InitStack(s);
	start.di = -1 ;// 开始点,且还没有尝试 ;
	a.Push(s,start);
	mg[start.x][start.y] = -1 ;
	while(!a.StackEmpty(s))
	{
		head;// 栈顶元素
		a.GetTop(s,head) ;
		if(head.x == end.x && head.y == end.y)
		{
			count++ ;
			printf("Map   %d :\n",count-1);
			for(int k = 0 ;k<=s->top ;k++)
			{
				printf("(%d ,%d) ",s->data[k].x,s->data[k].y);
				
				if((k+1)%5==0)   //输出上更好直观判断最短路径
				cout<<endl;
			}
			
			printf("\n\n");
			if(s->top+1 <minlen)
			{
				for(int k = 0 ;k<=s->top ;k++)
				{
					path[k] = s->data[k] ;
				}
				// 更新最短路径
				minlen = s->top+1 ;
			}
			// 退栈,重新走
			mg[s->data[s->top].x][s->data[s->top].y] = 0 ;
			s->top--;
			head.x = s->data[s->top].x ;
			head.y = s->data[s->top].y ;
			head.di = s->data[s->top].di ;
			
		}
		find = false ;
	
		while(head.di<4 && !find)
		{
			head.di++ ;
			switch(head.di){
				
				case 0:head.x=s->data[s->top].x -1 ;head.y =s->data[s->top].y;break;//上面
 
                case 1:head.x=s->data[s->top].x ;head.y =s->data[s->top].y+1;break;//右边
 
                case 2:head.x=s->data[s->top].x +1 ;head.y =s->data[s->top].y;break;//下面
 
                case 3:head.x=s->data[s->top].x  ;head.y =s->data[s->top].y-1;break;//左边
			}
				
			if(mg[head.x][head.y]==0)
			{
				find = true ;
			}
 
		}
		
		if(find)
		{
			//如果有路
			s->data[s->top].di = head.di ; // 修改原来栈顶的方向值
			s->top++;
			s->data[s->top].x = head.x ;// 入栈
			s->data[s->top].y = head.y ;
			s->data[s->top].di = -1 ;// 此点还没有进行过尝试
			mg[head.x][head.y] = -1 ;//访问过了
		}
		else
		{
			//回溯
			mg[s->data[s->top].x][s->data[s->top].y] = 0 ;
			s->top --;
		}
	
	}
		
		printf("最短路径长度为 :%d\n",minlen);
		printf("最短路径 :");
		for(int k = 0 ;k <minlen ;k++)
		{
			printf("(%d,%d)",path[k].x,path[k].y) ;
		}
		cout<<endl;
	
}
int main()
{
	Point start ,end ;
	start.x = 1 ;
	start.y = 1 ;
	end.x = 4 ;
	end.y = 4 ;
	dfs(start,end);
}

技术图片

6、求解栈元素排序问题

技术图片

#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>

#define MAX_SIZE 100

typedef char ElemType;
typedef struct
{
    ElemType data[MAX_SIZE];
    int top;   //栈顶指针
}SeqStack; 

//初始化顺序栈
static void init_stack(SeqStack *&s) 
{
    s = (SeqStack *)malloc(sizeof(SeqStack));
    s->top = -1;
}

//销毁顺序栈
static void destroy_stack(SeqStack *&s)
{
    free(s);
}

//判断栈空否
static bool stack_empty(SeqStack *s)
{
    return (s->top == -1);
}

//进栈
static bool push(SeqStack *&s, ElemType e)
{
    if(s->top == (MAX_SIZE - 1))   //栈满的情况,栈上溢出
        return false;
    s->top++;
    s->data[s->top] = e;
    return true;
}

//出栈
static bool pop(SeqStack *&s, ElemType &e) 
{
    if(s->top == -1)   //栈为空的情况,即栈下溢出
        return false;
    e = s->data[s->top];
    s->top--;
    return true;
}

//取栈顶元素
static bool get_top(SeqStack *s, ElemType &e)
{
    if(s->top == -1)   //栈为空的情况,即栈下溢出
        return false;
    e = s->data[s->top];
    return true;
}

//对栈中元素排序
/**
*   功能:对栈st中元素排序
*   @param st:要排序的栈
*   思路:
*       采用一个额外的栈tmpst存放临时数据。
*       处理st栈的某个栈顶元素e，出栈元素e，将其存放在tmpst中。若临时栈tmpst为空，直接
*   将e进入tmpst中；若tmpst栈不空，将它的元素退栈(放入st栈中)直到tmpst栈顶元素小于e，再
*   将tmp进入到tmpst中，进行这样的过程直到st为空，而tmpst中元素从栈底到栈顶是递增的。再
*   将tmpst中所有元素退栈并进栈到st中。
*/
static void sort(SeqStack *&st)
{
    SeqStack *tmpst;   //临时栈
    ElemType e, e1;
    init_stack(tmpst);   //初始化临时栈
    while(!stack_empty(st))   //st栈不空循环
    {
        pop(st, e);   //出栈元素e
        printf("    st:出栈%c=> ", e);
        while(!stack_empty(tmpst))   //tmpst栈不空循环
        {
            get_top(tmpst, e1);   //取栈顶元素e1
            printf("tmpst:取栈顶元素%c", e1);
            if(e1 > e)
            {
                printf("因%c>%c ", e1, e);
                printf("tmpst:退栈%c ", e1);
                pop(tmpst, e1);
                printf("s:进栈%c ", e1);
                push(st, e1);
            }
            else
            {
                printf("因%c<%c,退出循环", e1, e);
                break;
            }
        }
        push(tmpst, e);
        printf("tmpst:进栈%c\n", e);
    }
    while(!stack_empty(tmpst))
    {
        pop(tmpst, e);
        push(st, e);
    }
    destroy_stack(tmpst); 
}    

int main()
{
    ElemType e;
    SeqStack *s;

    init_stack(s);
    printf("(1)依次进栈元素1,3,4,2\n");
    push(s, ‘1‘);
    push(s, ‘3‘);
    push(s, ‘4‘);
    push(s, ‘2‘);
    printf("(2)栈s排序过程:\n");
    sort(s);
    printf("(3)栈s排序完毕\n");
    printf("(4)s的出栈序列:");
    while(!stack_empty(s))
    {
        pop(s, e);
        printf("%c ", e);
    }
    printf("\n");
    destroy_stack(s);
}

技术图片

7、用栈求解n皇后问题

技术图片

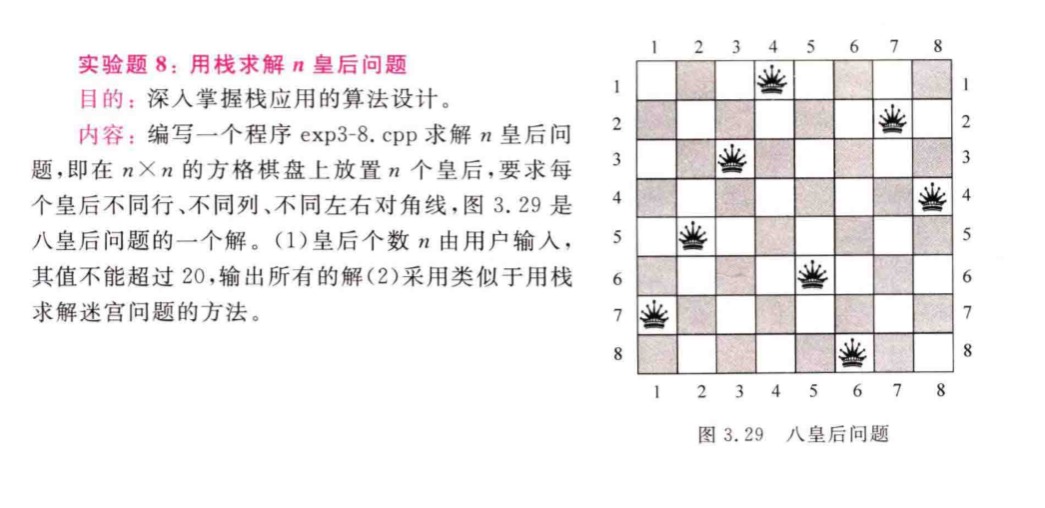
//学习于CSDN作者- _奶酪
#include <iostream>
#include <stdlib.h>
#include <cmath>
#include <algorithm>
using namespace std;
#define maxn 100

int n,num=1;//num定义为全局变量
typedef struct node {
    int col[maxn];//col[i]表示第i个n皇后的列数，（i，col[i])即为坐标
    int top;
}stacktype;

void display(stacktype st)
{
    printf("    第%d个解为：",num++);
    for(int i=1;i<=n;i++)
        printf("(%d,%d) ",i,st.col[i]);
    printf("\n");
}

bool place(stacktype st,int k,int j)
{
    int i=1;
    if(k==1) return true;   //第一个皇后直接放入，没有任何冲突
    while(i<=k-1)   //遍历前k-1个皇后，判断第k个皇后是否可以放在（k,j）处
    {
        if((st.col[i]==j)||(abs(st.col[i]-j)==abs(i-k)))
            return false;
        i++;
    }
    return true;
}
void queen(int n)
{
    int k;
    bool find;
    stacktype st;
    st.top=1;
    st.col[st.top]=0;
    while(st.top!=0)
    {
        k=st.top;   //记录栈顶皇后的个数
        find=false;
        for(int j=st.col[k]+1;j<=n;j++)   //回溯时要遍历当前列后面的列数，且下一个皇后的初始化列数为0
            if(place(st,k,j))
            {
                st.col[k]=j;
                find=true;
                break;   //找到第一个可以放入的位置
            }
        if(find)
        {
            if(k==n)
            {
                display(st);   //每次能放完n个皇后都要输出
            }
            else
            {
                st.top++;
                st.col[st.top]=0;
            }
        }
        else st.top--;   //回溯，最后while结束时是当第一个皇后放在（1，n)位置时无法将n个皇后都放下，st.top=0
    }
    if(num==1)
        printf("  此%d皇后问题无解!\n",n);
}
int main()
{
    printf("n皇后问题求解:n=");
    scanf("%d",&n);
    if(n>20) printf("n必须小于20\n");
    else
    {
        printf(" %d皇后问题的求解情况如下:\n",n);
        queen(n);
    }
}

技术图片

数据结构上机实验(3)

标签：tar   end   必须   class   回溯   开始   n皇后问题   lazy   坐标   

原文地址：https://www.cnblogs.com/wangzheming35/p/13170869.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！