标签:sdn 公式 nsf point 接下来 平移 ima https 直接
Computer Graphics note(1):变换
Games101清新脱俗,可惜没赶上直播。
官网:http://games-cn.org/intro-graphics/
结合食用:Fundamentals of Computer Graphics (3rd Edition) or (2nd Edition)
2D变换
对于能写成\(X^{‘}=MX\)形式的变换,称为线性变换(Linear Transforms),其中\(M\)为变换矩阵。
1.Scale(缩放)
基本的缩放就是沿着坐标轴进行的缩放,而对于xy轴任意比例缩放\(s_x,s_y\)而言,其数学形式如下:
\[\begin{cases}
x‘=s_x*x \y‘=s_y*y
\end{cases}
\]
转换为矩阵形式(\((x,y)^T\)左边的矩阵为变换矩阵)如下:
\[\begin{bmatrix}
x‘ \ y‘
\end{bmatrix}
=\begin{bmatrix}
s_x & 0\0 & s_y
\end{bmatrix}
\begin{bmatrix}
x \y
\end{bmatrix}
\]
例如下图为沿着xy轴都缩放0.5:

水平镜像也属于缩放操作,即\(s_x=-1,s_y=1\),其矩阵表示如下:
\[\begin{bmatrix}
x‘ \y‘
\end{bmatrix}=
\begin{bmatrix}
-1 & 0 \0 & 1
\end{bmatrix}
\begin{bmatrix}
x \y
\end{bmatrix}
\]
2.Shear(切变)
切变只变化一边,如下图所示:

可见,上面是变化了x轴,其矩阵形式如下:
\[\begin{bmatrix}
x‘ \y‘
\end{bmatrix}=
\begin{bmatrix}
1 & a \0 & 1
\end{bmatrix}
\begin{bmatrix}
x \y
\end{bmatrix}
\]
同理,对于变化y轴,其矩阵形式如下:
\[\begin{bmatrix}
x‘ \y‘
\end{bmatrix}=
\begin{bmatrix}
1 & 0 \a & 1
\end{bmatrix}
\begin{bmatrix}
x \y
\end{bmatrix}
\]
3.Rotate(旋转)
对于旋转而言,前提是默认绕原点旋转,方向为逆时针。\(x\)轴转转向\(y\)轴。
对于一个向量\(a\),其与\(x\)轴夹角为\(α\)假设要将其旋转角度\(φ\)得到向量\(b\),如下图所示(图来源:Fundamentals of Computer Graphics (3rd Edition) 6.1.3Rotation):

其旋转矩阵如下:
\[R(φ)
\begin{bmatrix}
cosφ & -sinφ \sinφ & cosφ
\end{bmatrix}
\]
推导过程1如下(来自Fundamentals of Computer Graphics (3rd Edition) 6.1.3Rotation):
假设向量\(a\)的长度为\(r\),则有
\[\begin{cases}
x_a=rcosα \y_a=rsinα
\end{cases}
\]
而\(b\)是\(a\)旋转得到的,所以长度相同,而其旋转角度为\((α+φ)\),则有
\[\begin{cases}
x_b=rcos(α+φ)=rcosαcosφ - rsinαsinφ \y_b=rsin(α+φ)=rsinαcosφ + rcosαsinφ
\end{cases}
\]
将上面的式子带入下面的式子可以得到如下结果:
\[\begin{cases}
x_b=x_acosφ - y_asinφ \y_b=y_acosφ + x_asinφ
\end{cases}
\]
所以最终的旋转矩阵如下:
\[R(φ)
\begin{bmatrix}
cosφ & -sinφ \sinφ & cosφ
\end{bmatrix}
\]
推导过程2(课程提及,辅助理解记忆)如下

考虑旋转矩阵对于任意点都适用,所以考虑几个特殊点的转换:\((1,0)->(cosθ,sinθ),(0,1)->(cosθ,-sinθ)\)。所以有下列关系:
\[\begin{cases}
\begin{bmatrix}
cosθ \sinθ
\end{bmatrix}
=\begin{bmatrix}
A & B\C & D
\end{bmatrix}
\begin{bmatrix}
1 \0
\end{bmatrix} \\\\begin{bmatrix}
-sinθ \cosθ
\end{bmatrix}
=\begin{bmatrix}
A & B\C & D
\end{bmatrix}
\begin{bmatrix}
0 \1
\end{bmatrix}
\end{cases}
\]
从中可以得到如下结果,即为所求:
\[\begin{cases}
A = cosθ \C = sinθ \B = -sinθ \D = cosθ \\end{cases}
\]
旋转矩阵的性质
考虑旋转\(R(-φ)\),会发现等于\(R_φ^T\),如下所示:
\[R(-φ)
\begin{bmatrix}
cosφ & -sinφ \sinφ & cosφ
\end{bmatrix}
=R_φ^T
\]
而从定义上看,\(R(-φ)\)=\(R_φ^{-1}\),所以可以得到\(R_φ^{-1}\)=\(R_φ^T\),即旋转矩阵的逆等于其转置矩阵,也就是说旋转矩阵为正交矩阵(数学意义)。
4.Translation(平移) & 齐次坐标
对于平移而言,即使考虑只有平移的情况,我们也只能写成如下形式:
对于平移:
\[\begin{cases}
x‘= x + t_x \y‘= y + t_y
\end{cases}
\]
其矩阵形式如下:
\[\begin{bmatrix}
x‘ \y‘
\end{bmatrix}
=\begin{bmatrix}
1 & 0 \0 & 1
\end{bmatrix}
\begin{bmatrix}
x \y
\end{bmatrix}+
\begin{bmatrix}
t_x \t_y
\end{bmatrix}
\]
为了让平移和上面的线性转换统一,引入齐次坐标。对于2D变换,增加一个维度\(w\),此时规定点和向量的齐次坐标表示如下:
\[point=(x,y,1)^T \vector=(x,y,0)^T
\]
即对于齐次坐标而言,\((x,y,w)^T(w!=0)\)表示的点即为\((\frac{x}{w},\frac{y}{w},1)^T\)。
则对于平移而言,其矩阵形式表示变为:
\[\begin{bmatrix}
x‘\y‘ \w‘
\end{bmatrix}
=\begin{bmatrix}
1 & 0 & t_x \0 & 1 & t_y \0 & 0 & 1 \\end{bmatrix}
\begin{bmatrix}
x \y \1
\end{bmatrix}
=\begin{bmatrix}
x+t_x \y+t_y \1
\end{bmatrix}
\]
这样一来形式就得到统一,并且使用齐次坐标还能保证以下操作的正确性:
\[vector +vector=vector; \point - point =vector;\point +vector =point;\\]
而对于\(point+point\)原本是无意义的,但是在齐次坐标下也能引申出其他意义,即两点相加为其中点,推导过程如下:
\[\begin{pmatrix}x_1 \\ y_1 \\ 1\end{pmatrix}
+\begin{pmatrix}x_2 \\y_2\\1 \end{pmatrix}
=\begin{pmatrix} x_1+x_2 \\y_1+y_2 \\ 2 \end{pmatrix}
=\begin{pmatrix}\frac{x_1+x_2}{2} \\ \frac{y_1+y_2}{2} \\ 1 \end{pmatrix}
\]
仿射变换 = 线性变换 +平移,即为
\[\begin{bmatrix}x‘ \\y‘\end{bmatrix} =
\begin{bmatrix}a&b \\c&d\end{bmatrix}
\begin{bmatrix}x \\y\end{bmatrix}
+
\begin{bmatrix}t_x \\t_y\end{bmatrix}
\]
使用齐次坐标表示如下:
\[\begin{bmatrix}x‘ \\y‘ \\ 1\end{bmatrix} =
\begin{bmatrix}a&b& t_x \c&d& t_y \\
0& 0& 1\end{bmatrix}
\begin{bmatrix}x \\y \\1\end{bmatrix}
\]
上面两者是等价的,所以仿射变换是先进行线性变换然后再进行的平移。
变换矩阵的结构性质
值得一提的是,当表示的是2D仿射变换的时候,上面的变换矩阵才有如下性质:
- 最后一行为\(0 0 1\)
- 最后一列的头两个数\(t_x,t_y\)必然表示平移
- 左上角四个数\(\begin{pmatrix}a&b \\ c & d\end{pmatrix}\)表示线性变换
齐次坐标下的变换矩阵
Scale:
\[S(S_x,S_y)=
\begin{bmatrix}
s_x & 0 & 0\0 & s_y & 0 \0&0&1
\end{bmatrix}
\]
Rotation:
\[R(φ)=
\begin{bmatrix}
cosφ & -sinφ & 0\sinφ & cosφ & 0\0 & 0& 1
\end{bmatrix}
\]
Translation:
\[T(t_x,t_y)=
\begin{bmatrix}
1 & 0 & t_x \0 & 1 & t_y \0 & 0 & 1 \\end{bmatrix}
\]
其他变换
逆变换即为原变换的相反操作,逆变换对应的变换矩阵即在数学意义上的逆矩阵,如下图中\(M^{-1}\)即为逆变换对应的变换矩阵,且逆矩阵有个基本性质,即\(MM^{-1}=I\),其中\(I\)为单位矩阵。

以下图为例子,假如想要从左边变换到右边的话,可以考虑的方式有先旋转再平移,或者先平移再旋转。

两种方式结果如下:

很明显,需要先旋转再平移,上面的变换过程用矩阵表示如下:
\[T_{1,0}·R_{45} \begin{bmatrix}x\\y\\1\end{bmatrix}
=\begin{bmatrix}
1 & 0& 1\0 &1&0 \0&0&1
\end{bmatrix}
\begin{bmatrix}
cos45 & -sin45 & 0 \sin45 & cos45 & 0 \0 & 0& 1
\end{bmatrix}
\begin{bmatrix}
x \\y\\1
\end{bmatrix}
\]
结论
- 以变换的顺序很重要,顺序不同结果也就不同。
- .变换矩阵应用的顺序是从右到左的。
上述结论可以推广,即当有\(N\)个变换矩阵\(A_1~A_n\)应用时,也是从右到左进行应用,同时因为矩阵满足结合律,所以我们可以先将前面的所有变换矩阵相乘(\(A_r=A_n···A_2A_1\)),然后再应用,结果是不变的。如下:
\[A_n···A_2A_1\begin{bmatrix}x\\y\\1\end{bmatrix} = A_r\begin{bmatrix}x\\y\\1\end{bmatrix}
\]
值得一提的是由于矩阵都是\(3X3\),所以即使前面的相乘,得到的矩阵\(A_r\)仍然是\(3X3\),也就是说一个矩阵也可以表示极为复杂的变换。
同时考虑仿射变换的性质,上面先旋转再平移也可以写成如下形式,结果不变:
\[T_{1,0}·R_{45} \begin{bmatrix}x\\y\\1\end{bmatrix}
=\begin{bmatrix}
cos45 & -sin45 & 1 \sin45 & cos45 & 0 \0 & 0& 1
\end{bmatrix}
\begin{bmatrix}
x \\y\\1
\end{bmatrix}
\]
变换的分解有多种多样,有时候不能一次性写出旋转矩阵,就可以将其分解,逐步应用变换矩阵来达到同样的效果。
例如考虑绕任意点\(c\)进行旋转,可以先将旋转中心移动到原点进行旋转之后再将旋转中心移动到\(c\)点。如下图所示:

其矩阵表示如下,应用过程从右到左:
\(T(c)·R(α)·T(-c)\)
3D变换
前提(右手系)
以下变换考虑的都是右手系(参考右手螺旋定则,四指弯曲方向为\(x\)旋转到\(y\)方向,大拇指方向为\(z\)方向)。
齐次坐标表示
类比2D中引入齐次坐标的原因,3D中的平移也不能直接写成,所以对于3D变换,增加一个维度\(w\),此时规定点和向量的齐次坐标表示如下:
\[point=(x,y,z,1)^T \vector=(x,y,z,0)^T
\]
同样的有对于齐次坐标而言,\((x,y,z,w)^T(w!=0)\)表示的点即为\((\frac{x}{w},\frac{y}{w},\frac{z}{w},1)^T\)。
矩阵描述3D中的仿射变换如下:
\[\begin{bmatrix}x‘ \\y‘ \\ z‘\\1\end{bmatrix} =
\begin{bmatrix}a&b&c& t_x \d&e&f& t_y \g&h&i& t_z \0& 0& 0&1\end{bmatrix}
\begin{bmatrix}x \\y \\z\\1\end{bmatrix}
\]
变换矩阵的结构性质
和2D中一样,当表示的是3D仿射变换的时候,上面的变换矩阵才有如下性质:
- 最后一行为\(0 0 01\)
- 最后一列的头两个数\(t_x,t_y,t_z\)必然表示平移
- 左上角9个数\(\begin{pmatrix}a&b&c \\ d&e&f \\ g&h&i \end{pmatrix}\)表示线性变换
齐次坐标下的变换矩阵
3D下和2D下的缩放和平移类似,但是旋转有些不同,
Scale:
\[S(S_x,S_y)=
\begin{bmatrix}
s_x & 0 & 0 &0\0 & s_y & 0 &0\0&0&s_z&0\0&0&0&1
\end{bmatrix}
\]
Translation:
\[T(t_x,t_y)=
\begin{bmatrix}
1 & 0 & 0&t_x \0 & 1 &0& t_y \0&0&1&t_z\0 & 0 & 0&1 \\end{bmatrix}
\]
Rotation
先考虑只绕一轴进行旋转的情况(绕谁谁不变),如下:
\[R_x(α)=\begin{bmatrix}
1 & 0 & 0&\0&cosα & -sinα & 0\0&sinα & cosα & 0\0&0&0&1
\end{bmatrix}\R_y(α)=\begin{bmatrix}
cosα & 0&sinα & 0\0&1&0&0\-sinα &0& cosα & 0\0&0&0&1
\end{bmatrix}\R_z(α)=\begin{bmatrix}
cosα & -sinα & 0&0\sinα & cosα & 0&0\0&0&1&0\0&0&0&1
\end{bmatrix}\\]
这里绕着\(y\)轴有所不同,这是因为我们使用的右手系,旋转方向默认逆时针的情况下,绕\(y\)轴,是\(z\)转向\(x\)方向,而矩阵定义的旋转顺序为\(xyz\),即为\(x\)->\(y\),\(y\)->\(z\),\(x\)->\(z\)。
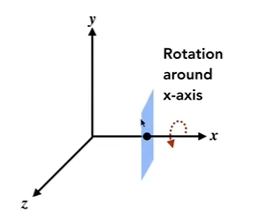
接下来简单总结一下一般情况绕任意轴下的3D旋转。
普通的3D旋转可以将其分解到绕\(xyz\)旋转,然后推导其公式(\(Rodrigues‘ Rotation Formula\))如下,其中\(\pmb{n}\)为旋转轴,\(α\)为旋转角,\(I\)为单位矩阵,这里默认沿着\(\pmb{n}\)旋转时,该轴是过原点的:
\[R(\pmb{n},α)=cos(α)\pmb{I}+(1-cos(α))\pmb{n}\pmb{n}^T+sin(α)
\begin{pmatrix}0 &-n_z&n_y\n_z&0&-n_z\-n_y&n_x&0\end{pmatrix}
\]
最右边的是向量叉积的矩阵形式。推导略。
Computer Graphics note(1):变换
标签:sdn 公式 nsf point 接下来 平移 ima https 直接
原文地址:https://www.cnblogs.com/FlyerBird/p/13171153.html








