P3065 [USACO12DEC]First! G

标签：tar   first   排序   https   地方   ++   loading   turn   str   

P3065 [USACO12DEC]First! G

题目大意：给你\(n\)个字符串，字符串的总长度不超过\(300000\)，问你在自定字典序的情况下有哪些字符串的字典序能够最小。

看到这道题第一想法是字典树和判环。字典树是存储字符串的方式，环则是判断矛盾的方式，考虑如何把这两个结合起来。

先看样例：

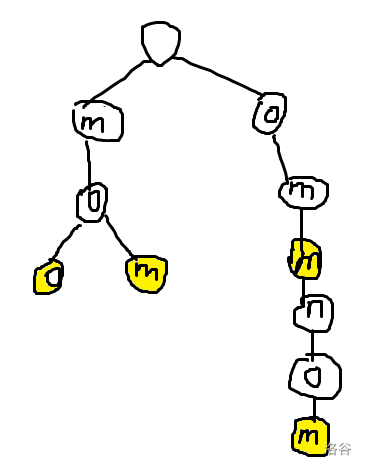
这里的话字典序能够最小的字符串有\(omm\)和\(mom\)。

当\(omm\)最小时，首先能想到的是和他有相同前缀的字符串\(ommnom\)。此时\(ommnon\)绝对不可能字典序最小，因为一定有比它更小的串。所以判断的第一个依据就是最小的字符串一定不会有别的串是他的前缀。考虑完这个以后，想到要使\(omm\)最小，则在第一个分叉处一定有能够判断字典序的大小关系，即\(o<m\)。

考虑如果\(mom\)最小时。在第一个分叉处有\(m<o\)，在第二个分叉处有\(m<o\)，两者并不矛盾，所以成立。

如果\(moo\)最小，则在第一个分叉处有\(m<o\)，第二个分叉处有\(m>o\)，两者矛盾，故不成立。那么判断的第二个依据就是字符串所代表的大小关系不矛盾。

于是可以得到一种做法：假设某个字符串是字典序最小的串，那么我们遍历这个字符串在字典树上的位置。如果他有前缀子串，则他不能作为最小字典序的字符串。同时在每处能够看出字典序大小关系的地方，即字典树的分叉处由小字符到大字符建边，最后判断是否出现环。有环则说明有矛盾，否则这个字符串就是成立的。找环用\(tarjan\)或者拓扑排序都可以。由于拓扑排序比较简单这里就用拓扑排序了。

以下是建图和判环的代码：

bool work(string c)
{
	int now = 0, len = c.size();
	for(int i = 0; i < len; i ++)
	{
		int a = c[i] - ‘a‘;
		if(flag[now]) return 1;//有前缀子串 
		for(int	 j = 0; j < 26; j ++)
		{
			if(ch[now][j] && j != a && !vis[a][j])
			//在分叉处建边 
			{
				vis[a][j] = 1;
				add(a, j);
				in[j] ++;
			}
		}
		now = ch[now][a];
	}
	return 0;
}
bool check()
{
	queue<int> q;
	//拓扑排序板子 
	for(int i = 0; i < 26; i ++) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int now = q.front();
		q.pop();
		for(int i = head[now]; i; i = edg[i].nxt)
		{
			in[edg[i].to] --;
			if(!in[edg[i].to]) q.push(edg[i].to);
		}
	}
	for(int i = 0; i < 26; i ++) if(in[i]) return 0;
	return 1;
}

P3065 [USACO12DEC]First! G

标签：tar   first   排序   https   地方   ++   loading   turn   str   

原文地址：https://www.cnblogs.com/lcezych/p/13171375.html