【Codeforces Round #639 (Div. 2) C】Hilbert's Hotel

标签：include   for   turn   can   pac   using   ber   移动   name   

题目链接

点我呀

翻译

一个旅馆内有无限多个房间, 每个房间里面都只有一个人住。

这些房间和所有的整数对应。

现在对于房间号为整数 \(k\) 的房间, 里面的人要移动到 \(k + a_{k\ mod\ n}\) 号房间。

给你 \(n\), 和整型数组 \(a\) , 问你移动之后, 是不是每个人都只占据一个房间, 以及每个房间是不是都没有空。

题解

这题就特别明显, 是想让你把 \(0\) ~ \(n-1\) 这些位置的房间, 加上对应的 \(a\) 值之后, 再对 \(n\) 取余, 得到结果 x。

对于 x, 只要 \(0\) ~ \(n-1\) 每个数字都只出现了一次的话, 就一定不会出现两个以上的人重叠在一起了。

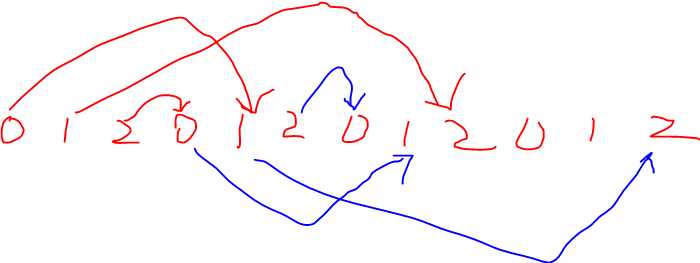
可以看看下图, 下图中红线是头 3 个人在换房间之后的结果, 蓝线是紧接着的 3 个人换房间的结果。每 n 个人换的

时候, 跨越的人都是一样的, 所以第一批的 n 个人不重复的话, 后面肯定也不会重复。

代码

#include<bits/stdc++.h>
#define ll long long
#define rei(x) scanf("%d",&x)
#define rel(x) scanf("%I64d",&x)
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
using namespace std;

const int N = 2e5;
const int MOD = 998244353;

int T, n;
int a[N+10];

int main(){
    #ifdef LOCAL_DEFINE
        freopen("D:\\rush.txt","r",stdin);
    #endif
    ios::sync_with_stdio(0),cin.tie(0);
    for (cin >> T;T > 0;T--){
        cin >> n;
        bool ok = true;
        rep1(i,0, n - 1){
            int x;
            cin >> x;
            x = ((x % n) + n) % n;
            x = (i + x) % n;
            if ( a[x] == T){
                ok = false;
            }else{
                a[x] = T;
            }
        }
        if (ok){
            cout << "YES" << endl;
        }else{
            cout << "NO" << endl;
        }
    }
    return 0;
}

【Codeforces Round #639 (Div. 2) C】Hilbert's Hotel

标签：include   for   turn   can   pac   using   ber   移动   name   

原文地址：https://www.cnblogs.com/AWCXV/p/13172146.html