标签:uniq letter oss tab oid img lis https order
周赛地址(英):Weekly Contest 194
周赛地址(中):第 194 场周赛
仓库地址:week-Leetcode
Given an integer n and an integer start.
Define an array nums where nums[i] = start + 2*i (0-indexed) and n == nums.length.
Return the bitwise XOR of all elements of nums.
Example 1:
Input: n = 5, start = 0
Output: 8
Explanation: Array nums is equal to [0, 2, 4, 6, 8] where (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8.
Where "^" corresponds to bitwise XOR operator.
Example 2:
Input: n = 4, start = 3
Output: 8
Explanation: Array nums is equal to [3, 5, 7, 9] where (3 ^ 5 ^ 7 ^ 9) = 8.
Example 3:
Input: n = 1, start = 7
Output: 7
Example 4:
Input: n = 10, start = 5
Output: 2
Constraints:
/**
* @param {number} n
* @param {number} start
* @return {number}
*/
const xorOperation = function(n, start) {
let ans=0
for(let i=0;i<n;i++){
ans^=start+2*i
}
return ans;
};
Given an array of strings names of size n. You will create n folders in your file system such that, at the ith minute, you will create a folder with the name names[i].
Since two files cannot have the same name, if you enter a folder name which is previously used, the system will have a suffix addition to its name in the form of (k), where, k is the smallest positive integer such that the obtained name remains unique.
Return an array of strings of length n where ans[i] is the actual name the system will assign to the ith folder when you create it.
Example 1:
Input: names = ["pes","fifa","gta","pes(2019)"]
Output: ["pes","fifa","gta","pes(2019)"]
Explanation: Let‘s see how the file system creates folder names:
"pes" --> not assigned before, remains "pes"
"fifa" --> not assigned before, remains "fifa"
"gta" --> not assigned before, remains "gta"
"pes(2019)" --> not assigned before, remains "pes(2019)"
Example 2:
Input: names = ["gta","gta(1)","gta","avalon"]
Output: ["gta","gta(1)","gta(2)","avalon"]
Explanation: Let‘s see how the file system creates folder names:
"gta" --> not assigned before, remains "gta"
"gta(1)" --> not assigned before, remains "gta(1)"
"gta" --> the name is reserved, system adds (k), since "gta(1)" is also reserved, systems put k = 2. it becomes "gta(2)"
"avalon" --> not assigned before, remains "avalon"
Example 3:
Input: names = ["onepiece","onepiece(1)","onepiece(2)","onepiece(3)","onepiece"]
Output: ["onepiece","onepiece(1)","onepiece(2)","onepiece(3)","onepiece(4)"]
Explanation: When the last folder is created, the smallest positive valid k is 4, and it becomes "onepiece(4)".
Example 4:
Input: names = ["wano","wano","wano","wano"]
Output: ["wano","wano(1)","wano(2)","wano(3)"]
Explanation: Just increase the value of k each time you create folder "wano".
Example 5:
Input: names = ["kaido","kaido(1)","kaido","kaido(1)"]
Output: ["kaido","kaido(1)","kaido(2)","kaido(1)(1)"]
Explanation: Please note that system adds the suffix (k) to current name even it contained the same suffix before.
Constraints:
//1.创建一个map,用来存储的name
// 2.遍历names,如果当前项在map中没有,则存储进去。否则在当前name后加index继续判断是否在map中
/**
* @param {string[]} names
* @return {string[]}
*/
const getFolderNames = function(names) {
let map=new Map();
for(let i=0;i<names.length;i++){
// 如果当前name不存在于map中,则加入至map
if(!map.get(names[i])){
map.set(names[i],true)
}else{
let index=1;
let newName=names[i]+`(${index})`
// index递增, 暴力比较文件名
while(map.get(newName)){
newName=names[i]+`(${++index})`
}
names[i]=newName
map.set(names[i],true)
}
}
return names
};
Your country has an infinite number of lakes. Initially, all the lakes are empty, but when it rains over the nth lake, the nth lake becomes full of water. If it rains over a lake which is full of water, there will be a flood. Your goal is to avoid the flood in any lake.
Given an integer array rains where:
rains[i] > 0 means there will be rains over the rains[i] lake.
rains[i] == 0 means there are no rains this day and you can choose one lake this day and dry it.
Return an array ans where:
ans.length == rains.length
ans[i] == -1 if rains[i] > 0.
ans[i] is the lake you choose to dry in the ith day if rains[i] == 0.
If there are multiple valid answers return any of them. If it is impossible to avoid flood return an empty array.
Notice that if you chose to dry a full lake, it becomes empty, but if you chose to dry an empty lake, nothing changes. (see example 4)
Example 1:
Input: rains = [1,2,3,4]
Output: [-1,-1,-1,-1]
Explanation: After the first day full lakes are [1]
After the second day full lakes are [1,2]
After the third day full lakes are [1,2,3]
After the fourth day full lakes are [1,2,3,4]
There‘s no day to dry any lake and there is no flood in any lake.
Example 2:
Input: rains = [1,2,0,0,2,1]
Output: [-1,-1,2,1,-1,-1]
Explanation: After the first day full lakes are [1]
After the second day full lakes are [1,2]
After the third day, we dry lake 2. Full lakes are [1]
After the fourth day, we dry lake 1. There is no full lakes.
After the fifth day, full lakes are [2].
After the sixth day, full lakes are [1,2].
It is easy that this scenario is flood-free. [-1,-1,1,2,-1,-1] is another acceptable scenario.
Example 3:
Input: rains = [1,2,0,1,2]
Output: []
Explanation: After the second day, full lakes are [1,2]. We have to dry one lake in the third day.
After that, it will rain over lakes [1,2]. It‘s easy to prove that no matter which lake you choose to dry in the 3rd day, the other one will flood.
Example 4:
Input: rains = [69,0,0,0,69]
Output: [-1,69,1,1,-1]
Explanation: Any solution on one of the forms [-1,69,x,y,-1], [-1,x,69,y,-1] or [-1,x,y,69,-1] is acceptable where 1 <= x,y <= 10^9
Example 5:
Input: rains = [10,20,20]
Output: []
Explanation: It will rain over lake 20 two consecutive days. There is no chance to dry any lake.
Constraints:
const avoidFlood = function(rains) {
let ans = new Array(rains.length).fill(-1)
let fullLakes = new Map()
let dryDays = new Set()
for (let i = 0; i < rains.length; i++){
if (rains[i] === 0) {
dryDays.add(i)
ans[i] = 0
} else {
if (!fullLakes.has(rains[i])) {
fullLakes.set(rains[i], i)
} else {
let previous = fullLakes.get(rains[i])
if (dryDays.size === 0) return []
let dryLake = false
for(let day of dryDays.keys()){
if (previous < day && day < i){
ans[day] = rains[i]
dryDays.delete(day)
fullLakes.set(rains[i], i)
dryLake = true
break
}
}
if (!dryLake){
return []
}
}
}
}
ans=ans.map(item=>{
if(item===0) item=1
return item;
})
return ans
}
Given a weighted undirected connected graph with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between nodes fromi and toi. A minimum spanning tree (MST) is a subset of the edges of the graph that connects all vertices without cycles and with the minimum possible total edge weight.
Find all the critical and pseudo-critical edges in the minimum spanning tree (MST) of the given graph. An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. A pseudo-critical edge, on the other hand, is that which can appear in some MSTs but not all.
Note that you can return the indices of the edges in any order.
Example 1:
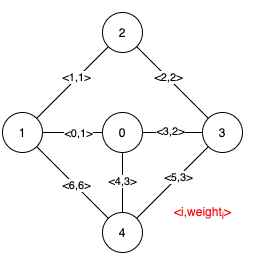
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:
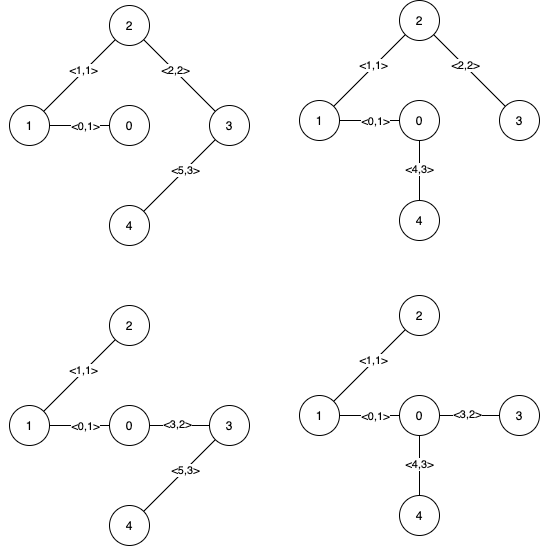
Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output.
The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.
Example 2:
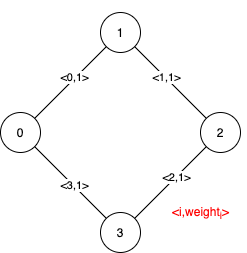
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.
Constraints:
2 <= n <= 100
1 <= edges.length <= min(200, n * (n - 1) / 2)
edges[i].length == 3
0 <= fromi < toi < n
1 <= weighti <= 1000
All pairs (fromi, toi) are distinct.
class Solution {
find(u, parent) {
while(parent[u]>=0)
u=parent[u];
return u;
}
MST(parent, edges, e, n, init) {
let edge=init;
let curr=0;
let minCost=0;
while(edge<n && curr<edges.length) {
let u=this.find(edges[e[curr][1]][0], parent);
let v=this.find(edges[e[curr][1]][1], parent);
if(v!=u){
minCost+=e[curr][0];
parent[u]=v;
++edge;
}
++curr;
}
return minCost;
}
List( n, edges) {
let e=[]
for(let i=0; i<edges.length; i++) {
e[i]=[]
e[i][0]=edges[i][2];
e[i][1]=i;
}
e.sort((a,b)=>a[0]-b[0])
let parent=new Array(n).fill(-1);
let minCost=this.MST(parent, edges, e, n, 1);
let poss=[]
for(let i=0; i<e.length; i++) {
parent=new Array(n).fill(-1)
parent[edges[e[i][1]][0]]=edges[e[i][1]][1];
let val=this.MST(parent, edges, e, n, 2)+e[i][0];
if(val==minCost)
poss.push(e[i][1]);
}
let result=[]
result[0]=[]
result[1]=[]
for(let i=0; i<poss.length; i++) {
parent=new Array(n).fill(-1)
let cost=0;
let edge=0;
let m=poss[i];
for(let j=0; j<poss.length; j++) {
if(i!=j) {
let node=poss[j];
let u=this.find(edges[node][0], parent);
let v=this.find(edges[node][1], parent);
if(u!=v) {
parent[u]=v;
++edge;
cost+=edges[node][2];
}
}
}
if(edge<n-1 || cost>minCost)
result[0].push(m)
else
result[1].push(m);
}
return result;
}
}
const findCriticalAndPseudoCriticalEdges = function(n, edges) {
let ans=new Solution();
return ans.List(n,edges)
};
标签:uniq letter oss tab oid img lis https order
原文地址:https://www.cnblogs.com/xingguozhiming/p/13173439.html