全景拼接学习-原理篇 (2) 两张图片之间关系计算 单应性Homograph估计

标签：变换   刚体   基本   amp   等于   inf   特征   matrix   bin   

教程 https://zhuanlan.zhihu.com/p/74597564

 目录
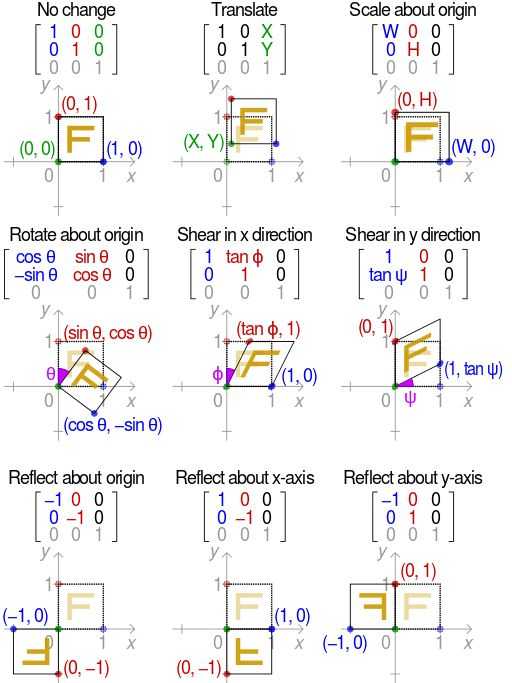
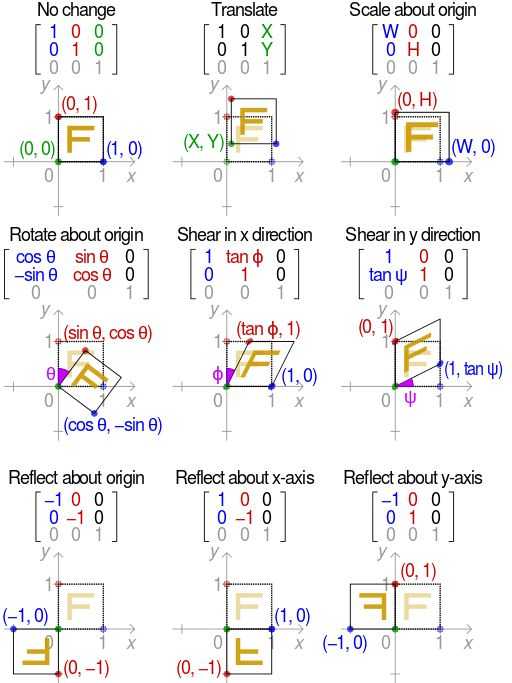
一 图像变换与平面坐标系的关系
二 平面坐标系与齐次坐标系
三 单应性变换

一 图像变换与平面坐标系的关系

• 旋转：

 写成矩阵乘法形式：

• 平移：

 但是现在遇到困难了，平移无法写成和上面旋转一样的矩阵乘法形式。所以引入齐次坐标  ，再写成矩阵形式：

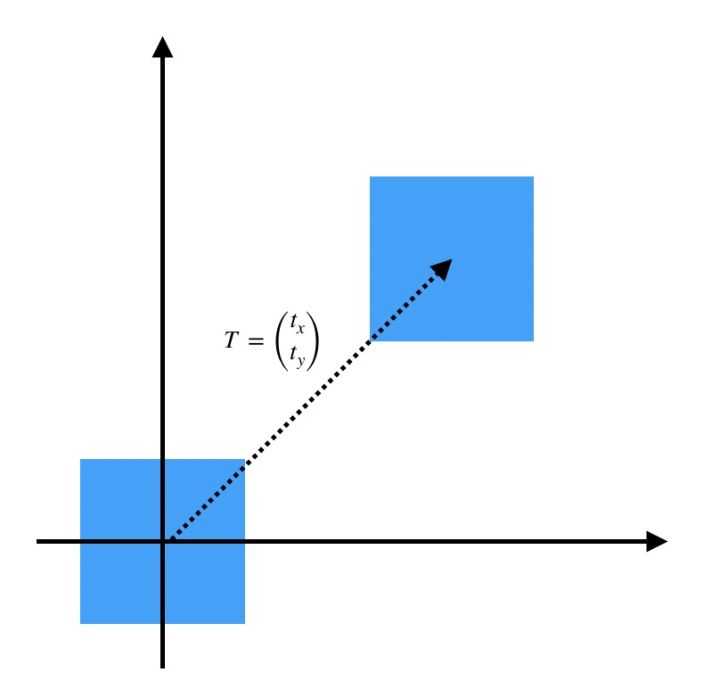
 其中  表示单位矩阵，而  表示平移向量。

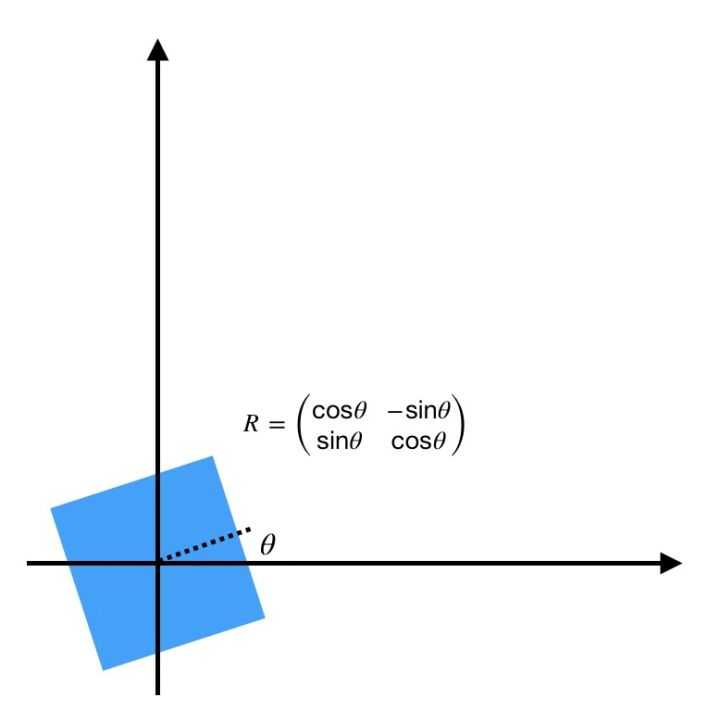
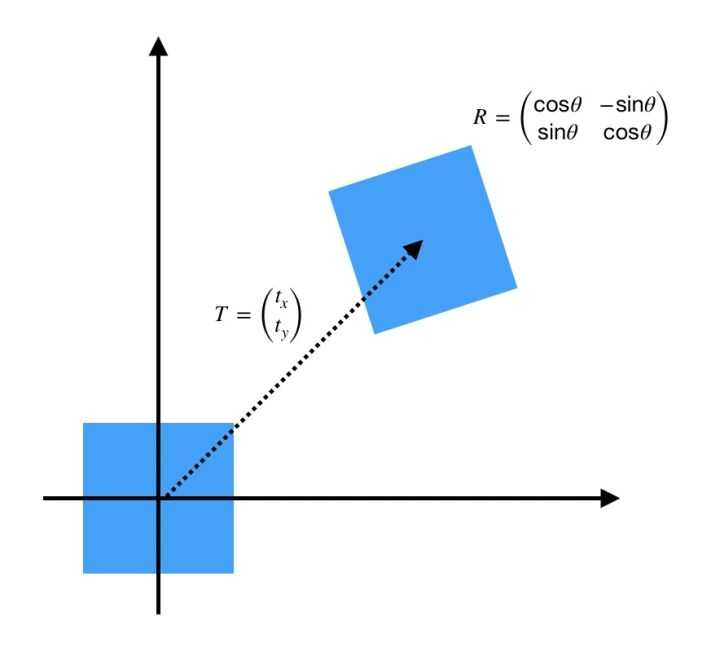
那么就可以把把旋转和平移统一写在一个矩阵乘法公式中，即刚体变换：

 而旋转矩阵  是正交矩阵（  ）。

刚体变换：旋转+平移（正方形-正方形）

作用：z轴距离不变 x  y 和原来相等  

仿射变换

作用：z轴距离不变 x  y 各自被比例拉伸 

 其中  可以是任意2x2矩阵（与  一定是正交矩阵不同）。

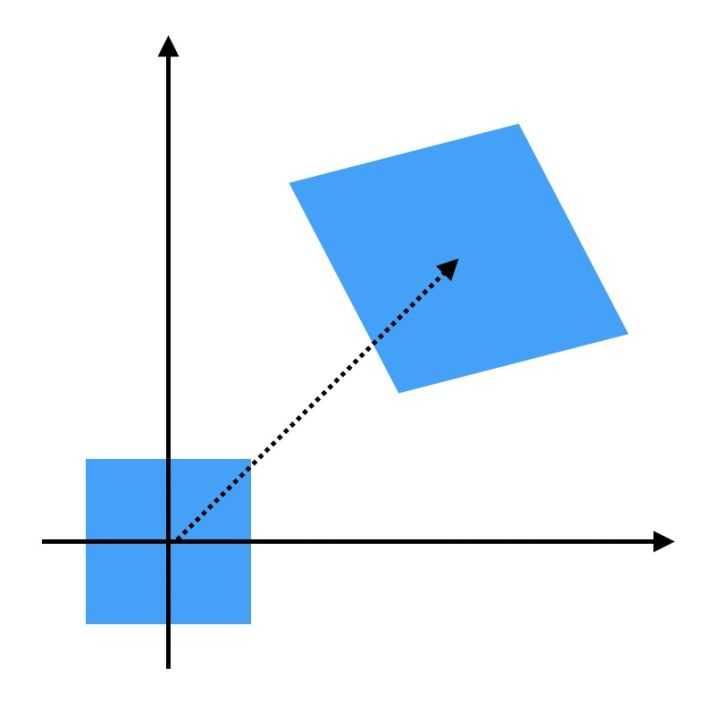
 仿射变换（正方形-平行四边形）

可以看到，相比刚体变换（旋转和平移），仿射变换除了改变目标位置，还改变目标的形状，但是会保持物体的“平直性”。

不同  和  矩阵对应的各种基本仿射变换：

仿射变换（正方形-平行四边形）

 可以看到，相比刚体变换（旋转和平移），仿射变换除了改变目标位置，还改变目标的形状，但是会保持物体的“平直性”。

不同  和  矩阵对应的各种基本仿射变换：

• 投影变换（单应性变换）

投影变换（单应性变换）

作用：z轴距离被拉伸   x  y 被比例拉伸  z

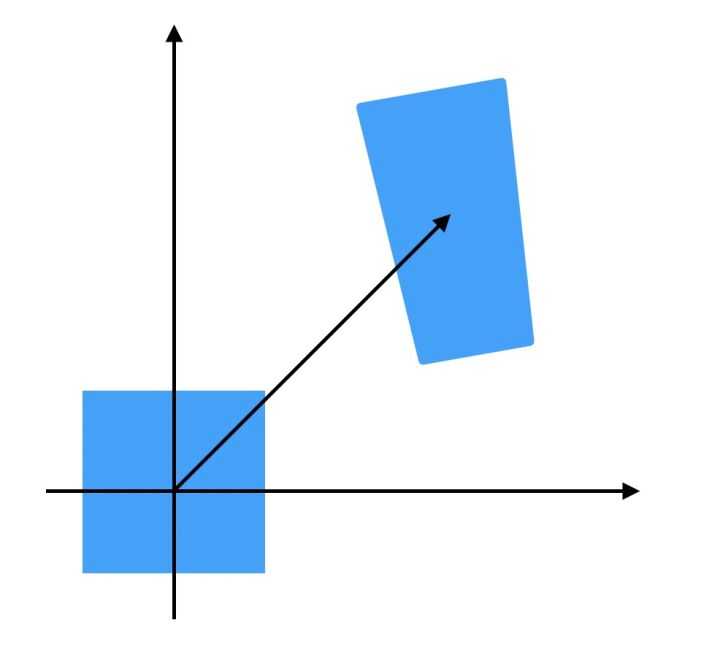
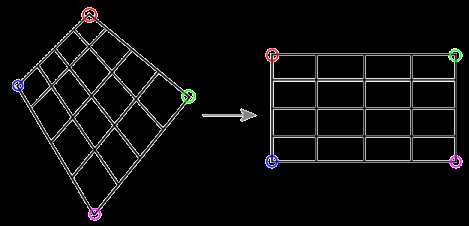
 投影变换（正方形-任意四边形）

总结一下：

1. 刚体变换：平移+旋转，只改变物体位置，不改变物体形状  x y  z等于原来
2. 仿射变换：改变物体位置和形状，但是保持“平直性”    z不变  x y 被比例拉伸
3. 投影变换：彻底改变物体位置和形状                         z  x y 都被比例拉伸

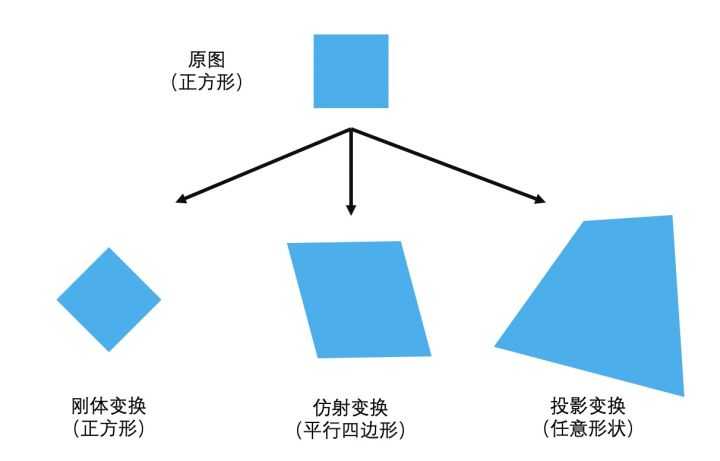
 注：上图“投影变换”应该是“任意四边形”

我们来看看完整投影变换矩阵各个参数的物理含义：

 其中  代表仿射变换参数

  代表平移变换参数

  表示一种“变换后边缘交点“关系，如：

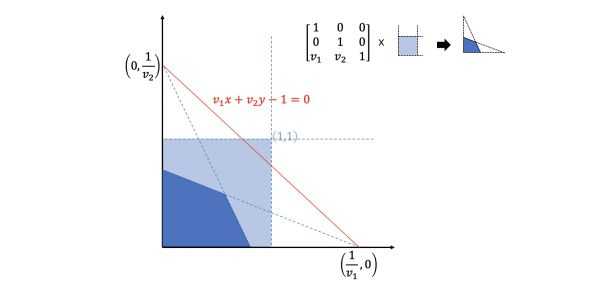
至于  则是一个与  相关的缩放因子。

一般情况下都会通过归一化使得  （原因见下文）。

二 平面坐标系与齐次坐标系

问题来了，齐次坐标到底是什么？

齐次坐标系  与常见的三维空间坐标系  不同，只有两个自由度：

而  （其中  ）对应坐标  和  的缩放尺度。当  时：

特别的当  时，对应无穷远：

三 单应性变换

• 单应性是什么？

此处不经证明的给出：同一个 [无镜头畸变] 的相机从不同位置拍摄 [同一平面物体] 的图像之间存在单应性，可以用 [投影变换] 表示 。

注意：单应性成立是有条件的！

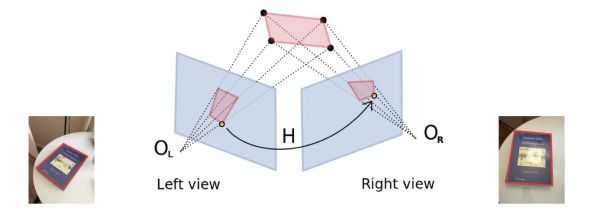
简单说就是：

其中  是Left view图片上的点，  是Right view图片上对应的点。

• 那么这个  单应性矩阵如何求解呢？

更一般的，每一组匹配点  有

由平面坐标与齐次坐标对应关系  ，上式可以表示为：

进一步变换为：

写成矩阵  形式：

也就是说一组匹配点  可以获得2组方程。

• 单应性矩阵8自由度

注意观察：单应性矩阵  与  其实完全一样（其中 ），例如：

即点  无论经过  还是  映射，变化后都是  。

如果使  ，那么有:

所以单应性矩阵  虽然有9个未知数，但只有8个自由度。

在求  时一般添加约束  （也有用  约束），所以还有  共8个未知数。由于一组匹配点  对应2组方程，那么只需要  组不共线的匹配点即可求解  的唯一解。

可以看到：

1. 红框所在平面上内容基本对齐，但受到镜头畸变影响无法完全对齐；
2. 平面外背景物体不符合单应性原理，偏离很大，完全无法对齐。

• 传统方法估计单应性矩阵

一般传统方法估计单应性变换矩阵，需要经过以下4个步骤：

1. 提取每张图SIFT/SURF/FAST/ORB等特征点
2. 提取每个特征点对应的描述子
3. 通过匹配特征点描述子，找到两张图中匹配的特征点对（这里可能存在错误匹配）
4. 使用RANSAC算法剔除错误匹配
5. 求解方程组，计算Homograph单应性变换矩阵

全景拼接学习-原理篇 (2) 两张图片之间关系计算 单应性Homograph估计

标签：变换   刚体   基本   amp   等于   inf   特征   matrix   bin   

原文地址：https://www.cnblogs.com/kekeoutlook/p/13179442.html