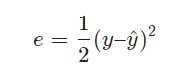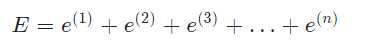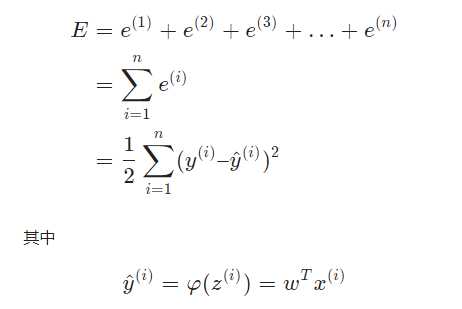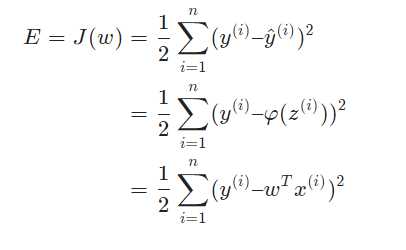梯度下降法的分类
批量梯度下降(Batch gradient descent)
上面使用的梯度下降法,每次都使用全量的训练集样本来更新模型参数,被称为批量梯度下降法。
批量梯度下降每次学习都使用整个训练集,因此其优点在于每次更新都会朝着正确的方向进行,最后能够保证收敛于极值点(凸函数收敛于全局极值点,非凸函数可能会收敛于局部极值点),但是其缺点在于每次学习时间过长,并且如果训练集很大以至于需要消耗大量的内存,并且批量梯度下降不能进行在线模型参数更新。
随机梯度下降(Stochastic gradient descent)
随机梯度下降算法每次从训练集中随机选择一个样本来进行学习。
批量梯度下降算法每次都会使用全部训练样本,因此这些计算是冗余的,因为每次都使用完全相同的样本集。而随机梯度下降算法每次只随机选择一个样本来更新模型参数,因此每次的学习是非常快速的,并且可以进行在线更新。
随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行,因此可以带来优化波动(扰动)。
不过从另一个方面来看,随机梯度下降所带来的波动有个好处就是,对于类似盆地区域(即很多局部极小值点)那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点,这样便可能对于非凸函数,最终收敛于一个较好的局部极值点,甚至全局极值点。
由于波动,因此会使得迭代次数(学习次数)增多,即收敛速度变慢。不过最终其会和全量梯度下降算法一样,具有相同的收敛性,即凸函数收敛于全局极值点,非凸损失函数收敛于局部极值点。
小批量梯度下降(Mini-batch gradient descent)
Mini-batch 梯度下降综合了 batch 梯度下降与 stochastic 梯度下降,在每次更新速度与更新次数中间取得一个平衡,其每次更新从训练集中随机选择 m, m < n 个样本进行学习。
相对于随机梯度下降,Mini-batch梯度下降降低了收敛波动性,即降低了参数更新的方差,使得更新更加稳定。相对于批量梯度下降,其提高了每次学习的速度。并且其不用担心内存瓶颈从而可以利用矩阵运算进行高效计算。一般而言每次更新随机选择[50,256]个样本进行学习,但是也要根据具体问题而选择,实践中可以进行多次试验,选择一个更新速度与更次次数都较适合的样本数。
深度学习 – 学习率
超参数
超参数是开发人员在构建模型时根据经验预先设置的参数,例如,网络层数,每层的神经元数量。
超参数不包括训练中学习的参数,例如,权重与偏置。
感知器和Adaline算法的超参数为:
- 学习率η
- epoch次数
学习率表示学习的速度,影响训练过程中,权重每次调整的值大小。
epoch是指一个完整的训练,即训练集中的数据都跑过一遍。
学习率选择
实践中,通常需要做一些实验,找到一个最适合的学习率η,可以让训练过程达到最优收敛。
学习率过小,导致收敛速度慢,步子小速度慢;学习率过大,导致找不到最小值点,步子太大跨过去了。

左边的图展示了最优学习率,成本函数可以快速收敛到全局最小值,但是如果学习率太小,收敛过程会变得很慢。
右边的图展示了,当选了一个很大的学习率,在调整权重时,有可能会跳过全局最小值。