复杂度

标签：complex   常见   维度   统计   依赖   忽略   复杂度   second   lis   

什么是算法？

1. 算法是用于解决特定问题的一系列的执行步骤；

1. 使用不同的算法，解决同一个问题，效率可能相差很大；

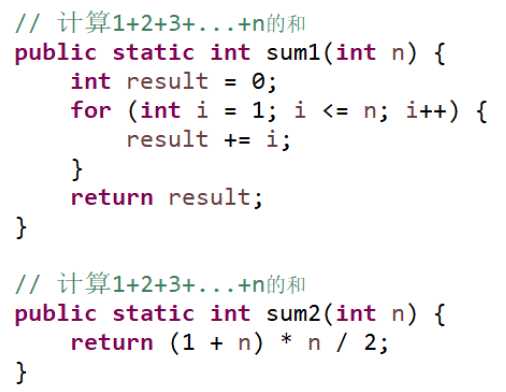
   • 比如：求第 n 个斐波那契数 （fibonacci number）  

      // 方法1
         public static int fib1(int n) {
             if (n <= 1) {
                 return 1;
             }
             return fib1(n - 1) + fib1(n - 2);
         }
     ?
         // 方法2
         public static int fib2(int n) {
             if (n <= 1) {
                 return 1;
             }
             int first = 0;
             int second = 1;
             for (int i = 0; i < n - 1; i++) {
                 int sum = first + second;
                 first = second;
                 second = sum;
             }
             return second;
         }

如何判断一个算法的好坏？

1. 如果单从执行效率上进行评估，可能会想到这么一种方案

   • 比较不同算法对同一组输入的执行处理时间

   • 这种方案也叫做：事后统计法；

2. 上述方案有比较明显的缺点

   • 执行时间严重依赖硬件以及运行时各种不确定的环境因素；

   • 必须编写相应的测算代码；

   • 测试数据的选择比较难保证公正性；

3. 一般从以下维度评估算法的优劣

   • 正确性、可读性、健壮性（对不合理的输入的反应能力和处理能力）

   • 时间复杂度（time complexity）：估算程序的执行次数（执行时间）；

   • 空间复杂度（space complexity）：估算所需占用的存储空间；

大 O 表示法：

1. 一般用大 O 表示法来描述复杂度，他表示的是数据规模 n 对应的复杂度；

2. 忽略常数、系数、低阶；

3. 注意：大 O 表示法仅仅是一种粗略的分析模型，是一种估算，能帮助我们短时间内了解一个算法的执行效率；

常见的复杂度：

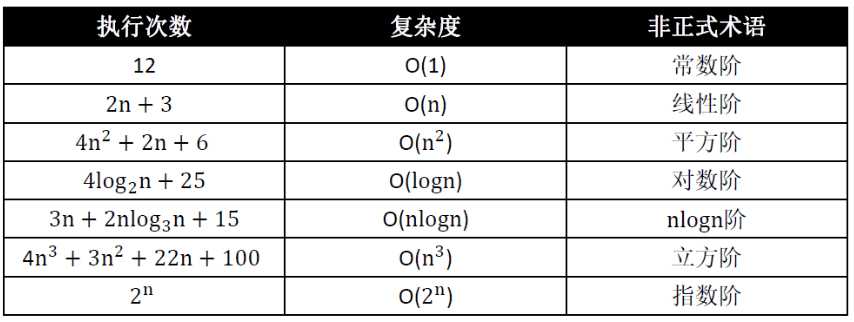
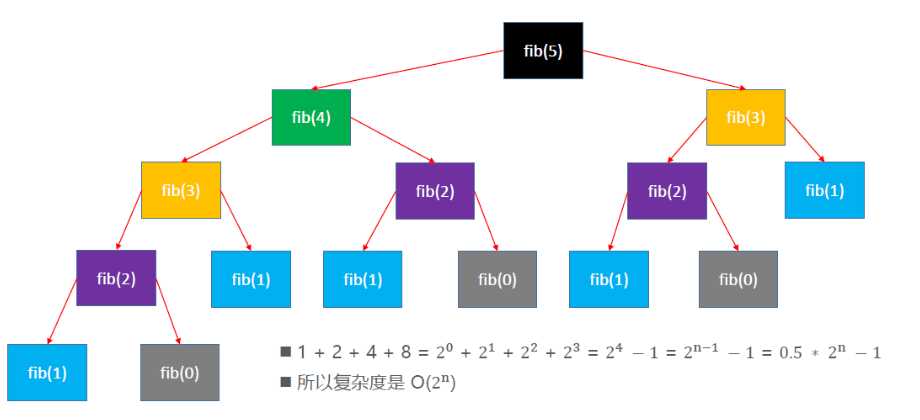
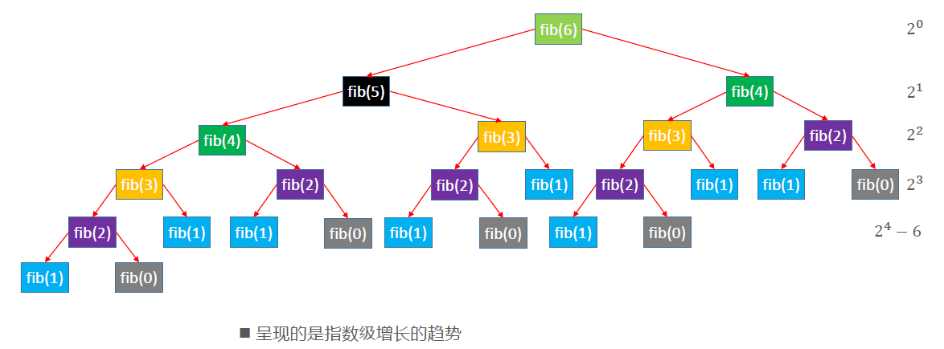
fib 函数的时间复杂度分析：

复杂度

标签：complex   常见   维度   统计   依赖   忽略   复杂度   second   lis   

原文地址：https://www.cnblogs.com/lililixuefei/p/13186157.html