标签:定义 strong 四种 ali 处理 可变 个数 alt 变量
随机变量定义:
? 随机变量是对每个实验结果指定一个数值的函数(随机试验E的样本空间S={e})
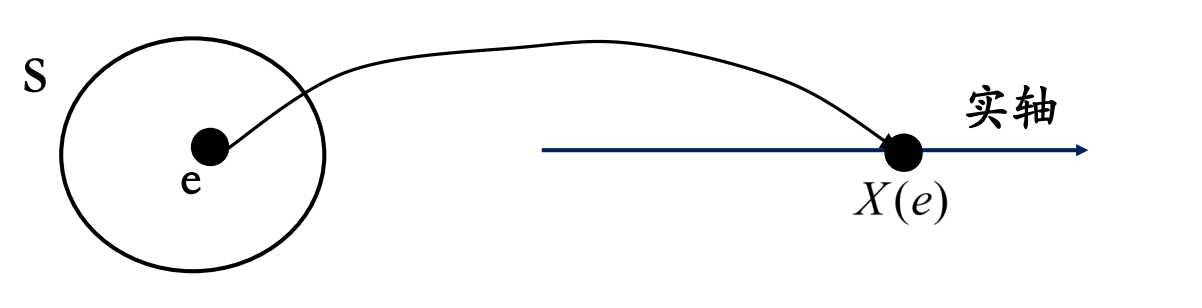
随机过程定义:
? 随机过程是对每个试验结果指定一个时间函数的函数。是t和e的二维函数。
? 随机过程是样本函数的集合。
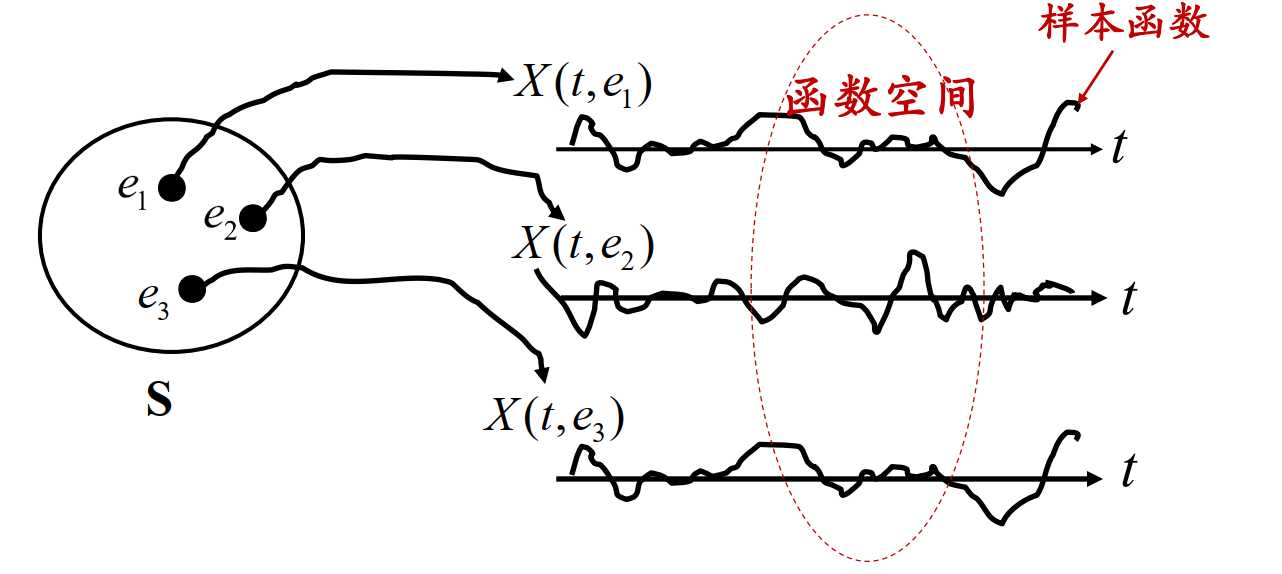
其中选定一个时间\(t_1\)时,\(X(t_1,e)\)是一个随机变量。随机过程是随时间变化的随机变量的集合。
举例:
? 随机相位信号 \(X(t) = Acos(\omega_ot + \Phi)\)
? \(A\)、\(\omega_0\)为常数, \(\Phi\subseteq U(0,2\pi)\)
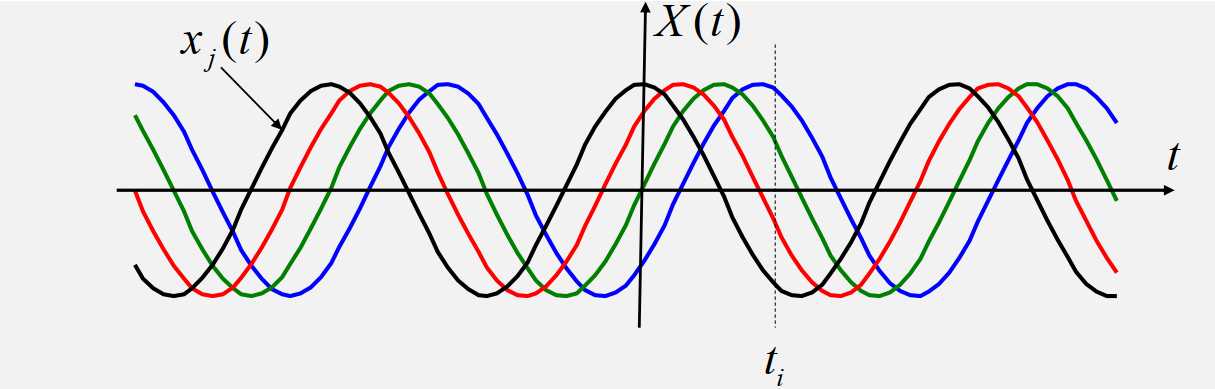
\(x_j(t) = Acos(\omega_0t + \phi_j)\to\)由\(\phi_j\)指定的一条样本函数
\(X(t_i)=Acos(\omega_0t_i+\Phi)\to\)随机变量
\(X(t,\Phi)\)四种不同情况下的意义:
| \(t\) | \(\phi\) | \(X(t)\) |
|---|---|---|
| 可变 | 固定 | 确定的时间函数 |
| 固定 | 可变 | 随机变量 |
| 固定 | 固定 | 确定的值 |
| 可变 | 可变 | 随机过程 |
随机过程的分类
根据时间和状态的不同,可以将随机过程划分为四类:
| 时间 | 状态 | |
|---|---|---|
| 连续时间随机过程 | 连续 | 连续 |
| 离散随机过程 | 连续 | 离散 |
| 离散随机序列 | 离散 | 离散 |
| 随机序列 | 离散 | 连续 |
序列——时间上不连续
根据样本函数的类型,可以将随机过程分为
? 确定形式的随机过程(如随机相位信号)——可预测过程
? 不规则形式的随机过程(如接收机噪声)——不可预测过程
随机过程可以表示为
任意随机过程 = 可预测过程 + 不可预测过程
参考:统计信号处理1.1.1节
标签:定义 strong 四种 ali 处理 可变 个数 alt 变量
原文地址:https://www.cnblogs.com/augustine0654/p/13189250.html