标签：引入   lin   添加   mda   type   mamicode   相机   logs   空间   

1.图优化的流程

1. 选择你想要的图里的节点与边的类型，确定它们的参数化形式；
2. 往图里加入实际的节点和边；
3. 选择初值，开始迭代；
4. 每一步迭代中，计算对应于当前估计值的雅可比矩阵和海塞矩阵；
5. 求解稀疏线性方程 H * detaX = -b，得到梯度方向；
6. 继续用GN或LM进行迭代。如果迭代结束，返回优化值。

　　实际上，g2o能帮你做好第3-6步，你要做的只是前两步而已。

2.顶点和边

• 在图中，以顶点表示优化变量，以边表示观测方程。

•  优化目标

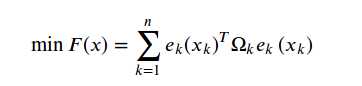
e(x,k) 是x符合z的程度的一个度量，越小越符合，反之越不符合。对式进行求导和一阶泰勒展开，得到其极值为0的方程：

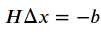
 其中，deta X即为梯度。

• 可解性解释

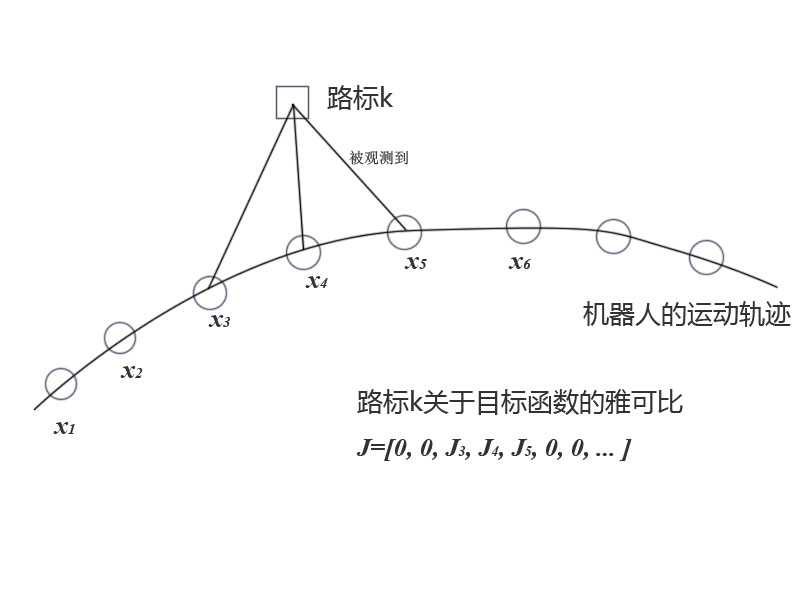
 只有和xk顶点相连的边，出现了非零值。相应的二阶导矩阵H中，大部分也是零元素。这种稀疏性能很好地帮助我们快速求解上面的线性方程。稀疏矩阵代数库：SBA、PCG、CSparse、Cholmod等等

•  引入核函数的原因，是因为SLAM中可能给出错误的边。如cauchy核，huber核等等。
• 问题： 四维变换矩阵T或者三维旋转矩R无法进行加减和求导：李群和李代数变换后可以，再变换回来。

2.g2o库

 3.应用

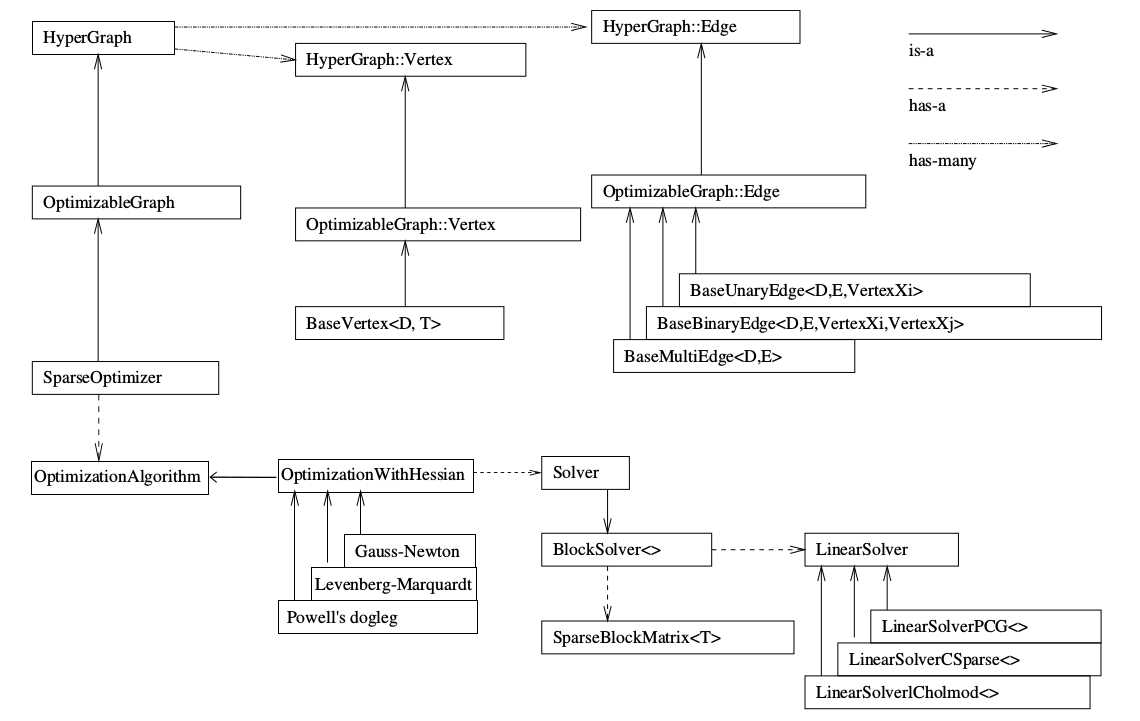
参考：https://www.cnblogs.com/gaoxiang12/p/5304272.html

1. 定义顶点
2. 定义边
3. 配置BlockSolver(LinerSolverType)
4. 配置OptimizationAlgorithm
5. 配置Optimizer
6. 添加顶点
7. 添加边
8. 启动优化

总结：

重要参考：https://www.cnblogs.com/gaoxiang12/p/5244828.html

https://www.aiimooc.com/mall/preshow-htm-itemid-382.html

图优化

标签：引入   lin   添加   mda   type   mamicode   相机   logs   空间   

原文地址：https://www.cnblogs.com/yrm1160029237/p/13189436.html