标签:莫名其妙 也会 png 个人 emacs tps lua 规律 表达式
怎样写一个解释器
文章来源 http://www.yinwang.org/blog-cn/2012/08/01/interpreter
写一个解释器,通常是设计和实现程序语言的第一步。解释器是简单却又深奥的东西,以至于好多人都不会写,所以我决定写一篇这方面的入门读物。
虽然我试图从最基本的原理讲起,尽量不依赖于其它知识,但这并不是一本编程入门教材。我假设你已经理解 Scheme 语言,以及基本的编程技巧(比如递归)。如果你完全不了解这些,那我建议你读一下 SICP 的第一,二章,或者 HtDP 的前几章,习题可以不做。注意不要读太多书,否则你就回不来了 ;-) 当然你也可以直接读这篇文章,有不懂的地方再去查资料。
实现语言容易犯的一个错误,就是一开头就试图去实现很复杂的语言(比如 JavaScript 或者 Python)。这样你很快就会因为这些语言的复杂性,以及各种历史遗留的设计问题而受到挫折,最后不了了之。学习实现语言,最好是从最简单,最干净的语言开始,迅速写出一个可用的解释器。之后再逐步往里面添加特性,同时保持正确。这样你才能有条不紊地构造出复杂的解释器。
因为这个原因,这篇文章只针对一个很简单的语言,名叫“R2”。它可以作为一个简单的计算器用,还具有变量定义,函数定义和调用等功能。
本文的解释器是用 Scheme 语言实现的。Scheme 有很多的“实现”,这里我用的实现叫做 Racket,它可以在这里免费下载。为了让程序简洁,我用了一点点 Racket 的模式匹配(pattern matching)功能。我对 Scheme 的实现没有特别的偏好,但 Racket 方便易用,适合教学。如果你用其它的 Scheme 实现,可能得自己做一些调整。
Racket 具有宏(macro),所以它其实可以变成很多种语言。如果你之前用过 DrRacket,那它的“语言设置”可能被你改成了 R5RS 之类的。所以如果下面的程序不能运行,你可能需要检查一下 DrRacket 的“语言设置”,把 Language 设置成 “Racket”。
Racket 允许使用方括号而不只是圆括号,所以你可以写这样的代码:
(let ([x 1]
[y 2])
(+ x y))
方括号跟圆括号可以互换,唯一的要求是方括号必须和方括号匹配。通常我喜欢用方括号来表示“无动作”的数据(比如上面的 [x 1], [y 2]),这样可以跟函数调用和其它具有“动作”的代码,产生“视觉差”。这对于代码的可读性是一个改善,因为到处都是圆括号的话,确实有点太单调,容易打瞌睡。
另外,Racket 程序的最上面都需要加上像 #lang racket 这样的语言选择标记,这样 Racket 才可以知道你想用哪个语言变种。
准备工作就到这里。现在我来谈一下,解释器到底是什么。说白了,解释器跟计算器差不多。解释器是一个函数,你输入一个“表达式”,它就输出一个 “值”,像这样:
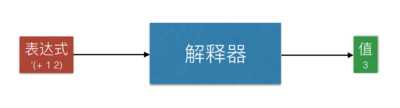
比如,你输入表达式 ‘(+ 1 2) ,它就输出值,整数3。表达式是一种“表象”或者“符号”,而值却更加接近“本质”或者“意义”。我们“解释”了符号,得到它的意义,这也许就是为什么它叫做“解释器”。
需要注意的是,表达式是一个数据结构,而不是一个字符串。我们用一种叫“S 表达式”(S-expression)的结构来存储表达式。比如表达式 ‘(+ 1 2) 其实是一个链表(list),它里面的内容是三个符号(symbol):+, 1 和 2,而不是字符串"(+ 1 2)"。
从 S 表达式这样的“结构化数据”里提取信息,方便又可靠,而从字符串里提取信息,麻烦而且容易出错。Scheme(Lisp)语言里面大量使用结构化数据,少用字符串,这是 Lisp 系统比 Unix 系统先进的地方之一。
从计算理论的角度讲,每个程序都是一台机器的“描述”,而解释器就是在“模拟”这台机器的运转,也就是在进行“计算”。所以从某种意义上讲,解释器就是计算的本质。当然,不同的解释器就会带来不同的计算。
CPU 也是一个解释器,它专门解释执行机器语言。如果你深刻理解了解释器,就可以从本质上看出各种 CPU 的设计为什么是那个样子,它们有什么优缺点,而不只是被动的作为它们的使用者。
用 S 表达式所表示的代码,本质上是一种叫做“树”(tree)的数据结构。更具体一点,这叫做“抽象语法树”(Abstract Syntax Tree,简称 AST)。下文为了简洁,我们省略掉“抽象”两个字,就叫它“语法树”。
跟普通的树结构一样,语法树里的节点,要么是一个“叶节点”,要么是一颗“子树”。叶节点是不能再细分的“原子”,比如数字,字符串,操作符,变量名。而子树是可以再细分的“结构”,比如算术表达式,函数定义,函数调用,等等。
举个简单的例子,表达式 ‘(* (+ 1 2) (+ 3 4)),就对应如下的语法树结构:
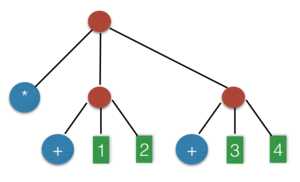
其中,*,两个+,1,2,3,4 都是叶节点,而那三个红色节点,都表示子树结构:‘(+ 1 2),‘(+ 3 4),‘(* (+ 1 2) (+ 3 4))。
在基础的数据结构课程里,我们都学过二叉树的遍历操作,也就是所谓先序遍历,中序遍历和后序遍历。语法树跟二叉树,其实没有很大区别,所以你也可以在它上面进行遍历。解释器的算法,就是在语法树上的一种遍历操作。由于这个渊源关系,我们先来做一个遍历二叉树的练习。做好了之后,我们就可以把这段代码扩展成一个解释器。
这个练习是这样:写出一个函数,名叫tree-sum,它对二叉树进行“求和”,把所有节点里的数加在一起,返回它们的和。举个例子,(tree-sum ‘((1 2) (3 4))),执行后应该返回 10。注意:这是一颗二叉树,所以不会含有长度超过 2 的子树,你不需要考虑像 ((1 2) (3 4 5)) 这类情况。需要考虑的例子是像这样:(1 2),(1 (2 3)), ((1 2) 3) ((1 2) (3 4)),……
(为了达到最好的学习效果,你最好试一下写出这个函数再继续往下看。)
好了,希望你得到了跟我差不多的结果。我的代码是这个样子:
#lang racket
(define tree-sum
(lambda (exp)
(match exp ; 对输入exp进行模式匹配
[(? number? x) x] ; exp是一个数x吗?如果是,那么返回这个数x
[`(,e1 ,e2) ; exp是一个含有两棵子树的中间节点吗?
(let ([v1 (tree-sum e1)] ; 递归调用tree-sum自己,对左子树e1求值
[v2 (tree-sum e2)]) ; 递归调用tree-sum自己,对右子树e2求值
(+ v1 v2))]))) ; 返回左右子树结果v1和v2的和
你可以通过以下的例子来测试它的正确性:
(tree-sum ‘(1 2))
;; => 3
(tree-sum ‘(1 (2 3)))
;; => 6
(tree-sum ‘((1 2) 3))
;; => 6
(tree-sum ‘((1 2) (3 4)))
;; => 10
(完整的代码和示例,可以在这里下载。)
这个算法很简单,我们可以把它用文字描述如下:
exp 是一个数,那就返回这个数。exp 是像 (,e1 ,e2) 这样的子树,那么分别对 e1 和 e2 递归调用 tree-sum,进行求和,得到 v1 和 v2,然后返回 v1 + v2 的和。你自己写出来的代码,也许用了 if 或者 cond 语句来进行分支,而我的代码里面使用的是 Racket 的模式匹配(match)。这个例子用 if 或者 cond 其实也可以,但我之后要把这代码扩展成一个解释器,所以提前使用了 match。这样跟后面的代码对比的时候,就更容易看出规律来。接下来,我就简单讲一下这个 match 表达式的工作原理。
现在不得不插入一点 Racket 的技术细节,如果你已经学会使用 Racket 的模式匹配,可以跳过这一节。你也可以通过阅读 Racket 模式匹配的文档来代替这一节。但我建议你不要读太多文档,因为我接下去只用到很少的模式匹配功能,我把它们都解释如下。
模式匹配的形式一般是这样:
(match x
[模式 结果]
[模式 结果]
... ...
)
它先对 x 求值,然后根据值的结构来进行分支。每个分支由两部分组成,左边是一个模式,右边是一个结果。整个 match 语句的语义是这样:从上到下依次考虑,找到第一个可以匹配 x 的值的模式,返回它右边的结果。左边的模式在匹配之后,可能会绑定一些变量,这些变量可以在右边的表达式里使用。
模式匹配是一种分支语句,它在逻辑上就是 Scheme(Lisp) 的 cond 表达式,或者 Java 的嵌套条件语句 if ... else if ... else ...。然而跟条件语句里的“条件”不同,每条 match 语句左边的模式,可以准确而形象地描述数据结构的形状,而且可以在匹配的同时,对结构里的成员进行“绑定”。这样我们可以在右边方便的访问结构成员,而不需要使用访问函数(accessor)或者 foo.x 这样的属性语法(attribute)。而且模式可以有嵌套的子结构,所以它能够一次性的表示复杂的数据结构。
举个实在点的例子。我的代码里用了这样一个 match 表达式:
(match exp
[(? number? x) x]
[`(,e1 ,e2)
(let ([v1 (tree-sum e1)]
[v2 (tree-sum e2)])
(+ v1 v2))])
第二行里面的 ‘(,e1 ,e2) 是一个模式(pattern),它被用来匹配 exp 的值。如果 exp 是 ‘(1 2),那么它与‘(,e1 ,e2)匹配的时候,就会把 e1 绑定到 ‘1,把 e2 绑定到 ‘2。这是因为它们结构相同:
`(,e1 ,e2)
‘( 1 2)
说白了,模式就是一个可以含有“名字”(像 e1 和 e2)的结构,像 ‘(,e1 ,e2)。我们拿这个带有名字的结构,去匹配实际数据,像 ‘(1 2)。当它们一一对应之后,这些名字就被绑定到数据里对应位置的值。
第一行的“模式”比较特殊,(? number? x) 表示的,其实是一个普通的条件判断,相当于 (number? exp),如果这个条件成立,那么它把 exp 的值绑定到 x,这样右边就可以用 x 来指代 exp。对于无法细分的结构(比如数字,布尔值),你只能用这种方式来“匹配”。看起来有点奇怪,不过习惯了就好了。
模式匹配对解释器和编译器的书写相当有用,因为程序的语法树往往具有嵌套的结构。不用模式匹配的话,往往要写冗长,复杂,不直观的代码,才能描述出期望的结构。而且由于结构的嵌套比较深,很容易漏掉边界情况,造成错误。模式匹配可以直观的描述期望的结构,避免漏掉边界情况,而且可以方便的访问结构成员。
由于这个原因,很多源于 ML 的语言(比如 OCaml,Haskell)都有模式匹配的功能。因为 ML(Meta-Language)原来设计的用途,就是用来实现程序语言的。Racket 的模式匹配也是部分受了 ML 的启发,实际上它们的原理是一模一样的。
好了,树遍历的练习就做到这里。然而这跟解释器有什么关系呢?下面我们只把它改一下,就可以得到一个简单的解释器。
计算器也是一种解释器,只不过它只能处理算术表达式。我们的下一个目标,就是写出一个计算器。如果你给它 ‘(* (+ 1 2) (+ 3 4)),它就输出 21。可不要小看这个计算器,稍后我们把它稍加改造,就可以得到一个更多功能的解释器。
上面的代码里,我们利用递归遍历,对树里的数字求和。那段代码里,其实已经隐藏了一个解释器的框架。你观察一下,一个算术表达式 ‘(* (+ 1 2) (+ 3 4)),跟二叉树 ‘((1 2) (3 4)) 有什么不同?发现没有,这个算术表达式比起二叉树,只不过在每个子树结构里多出了一个操作符:一个 * 和两个 + 。它不再是一棵二叉树,而是一种更通用的树结构。
这点区别,也就带来了二叉树求和与解释器算法的区别。对二叉树进行求和的时候,在每个子树节点,我们都做加法。而对表达式进行解释的时候,在每一个子树节点,我们不一定进行加法。根据子树的“操作符”不同,我们可能会选择加,减,乘,除四种操作。
好了,下面就是这个计算器的代码。它接受一个表达式,输出一个数字作为结果。
#lang racket ; 声明用 Racket 语言
(define calc
(lambda (exp)
(match exp ; 分支匹配:表达式的两种情况
[(? number? x) x] ; 是数字,直接返回
[`(,op ,e1 ,e2) ; 匹配提取操作符op和两个操作数e1,e2
(let ([v1 (calc e1)] ; 递归调用 calc 自己,得到 e1 的值
[v2 (calc e2)]) ; 递归调用 calc 自己,得到 e2 的值
(match op ; 分支匹配:操作符 op 的 4 种情况
[‘+ (+ v1 v2)] ; 如果是加号,输出结果为 (+ v1 v2)
[‘- (- v1 v2)] ; 如果是减号,乘号,除号,相似的处理
[‘* (* v1 v2)]
[‘/ (/ v1 v2)]))])))
你可以得到如下的结果:
(calc ‘(+ 1 2))
;; => 3
(calc ‘(* 2 3))
;; => 6
(calc ‘(* (+ 1 2) (+ 3 4)))
;; => 21
(完整的代码和示例,可以在这里下载。)
跟之前的二叉树求和代码比较一下,你会发现它们惊人的相似,因为解释器本来就是一个树遍历算法。不过你发现它们有什么不同吗?它们的不同点在于:
算术表达式的模式里面,多出了一个“操作符”(op)叶节点:(,op ,e1 ,e2)
对子树 e1 和 e2 分别求值之后,我们不是返回 (+ v1 v2),而是根据 op 的不同,返回不同的结果:
(match op
[‘+ (+ v1 v2)]
[‘- (- v1 v2)]
[‘* (* v1 v2)]
[‘/ (/ v1 v2)])
最后你发现,一个算术表达式的解释器,不过是一个稍加扩展的树遍历算法。
实现了一个计算器,现在让我们过渡到一种更强大的语言。为了方便称呼,我给它起了一个萌萌哒名字,叫 R2。R2 比起之前的计算器,只多出四个元素,它们分别是:变量,函数,绑定,调用。再加上之前介绍的算术操作,我们就得到一个很简单的程序语言,它只有5种不同的构造。用 Scheme 的语法,这5种构造看起来就像这样:
(其中,• 是一个算术操作符,可以选择 +, -, *, / 其中之一)
一般程序语言还有很多其它构造,可是一开头就试图去实现所有那些,只会让人糊涂。最好是把这少数几个东西搞清楚,确保它们正确之后,才慢慢加入其它元素。
这些构造的语义,跟 Scheme 里面的同名构造几乎一模一样。如果你不清楚什么是”绑定“,那你可以把它看成是普通语言里的”变量声明“。
需要注意的是,跟一般语言不同,我们的函数只接受一个参数。这不是一个严重的限制,因为在我们的语言里,函数可以被作为值传递,也就是所谓“first-class function”。所以你可以用嵌套的函数定义来表示有两个以上参数的函数。
举个例子, (lambda (x) (lambda (y) (+ x y))) 是个嵌套的函数定义,它也可以被看成是有两个参数(x 和 y)的函数,这个函数返回 x 和 y 的和。当这样的函数被调用的时候,需要两层调用,就像这样:
(((lambda (x)
(lambda (y) (+ x y)))
1)
2)
;; => 3
这种做法在PL术语里面,叫做咖喱(currying)。看起来啰嗦,但这样我们的解释器可以很简单。等我们理解了基本的解释器,再实现真正的多参数函数也不迟。
另外,我们的绑定语法 (let ([x e1]) e2),比起 Scheme 的绑定也有一些局限。我们的 let 只能绑定一个变量,而 Scheme 可以绑定多个,像这样 (let ([x 1] [y 2]) (+ x y))。这也不是一个严重的限制,因为我们可以啰嗦一点,用嵌套的 let 绑定:
(let ([x 1])
(let ([y 2])
(+ x y)))
下面是我们今天要完成的解释器,它可以运行一个 R2 程序。你可以先留意一下各部分的注释。
#lang racket
;;; 以下三个定义 env0, ext-env, lookup 是对环境(environment)的基本操作:
;; 空环境
(define env0 ‘())
;; 扩展。对环境 env 进行扩展,把 x 映射到 v,得到一个新的环境
(define ext-env
(lambda (x v env)
(cons `(,x . ,v) env)))
;; 查找。在环境中 env 中查找 x 的值。如果没找到就返回 #f
(define lookup
(lambda (x env)
(let ([p (assq x env)])
(cond
[(not p) #f]
[else (cdr p)]))))
;; 闭包的数据结构定义,包含一个函数定义 f 和它定义时所在的环境
(struct Closure (f env))
;; 解释器的递归定义(接受两个参数,表达式 exp 和环境 env)
;; 共 5 种情况(变量,函数,绑定,调用,数字,算术表达式)
(define interp
(lambda (exp env)
(match exp ; 对exp进行模式匹配
[(? symbol? x) ; 变量
(let ([v (lookup x env)])
(cond
[(not v)
(error "undefined variable" x)]
[else v]))]
[(? number? x) x] ; 数字
[`(lambda (,x) ,e) ; 函数
(Closure exp env)]
[`(let ([,x ,e1]) ,e2) ; 绑定
(let ([v1 (interp e1 env)])
(interp e2 (ext-env x v1 env)))]
[`(,e1 ,e2) ; 调用
(let ([v1 (interp e1 env)]
[v2 (interp e2 env)])
(match v1
[(Closure `(lambda (,x) ,e) env-save)
(interp e (ext-env x v2 env-save))]))]
[`(,op ,e1 ,e2) ; 算术表达式
(let ([v1 (interp e1 env)]
[v2 (interp