标签:取值 coding 强制 影响 nal mic 规划 输入 说明
linear-CRF第一个问题是评估推断(Inference),即给定 linear-CRF的条件概率分布P(y|x), 在给定输入序列x和输出序列y时,计算条件概率P(yi|x)和P(yi−1,yi|x)以及对应的期望。
要计算条件概率,我们也可以使用和HMM类似的方法(也是分成左右两个部分,分别进行求解),使用前向后向算法来完成。首先我们来看前向概率的计算。
我们定义 αi(yi|x)表示序列位置 i 的标记是 时,在位置 i 之前的部分标记序列的非规范化概率。之所以是非规范化概率是因为我们不想加入一个不影响结果计算的规范化因子Z(x) 在分母里面。
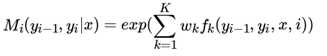
这个式子定义了在给定 时,从的非规范化概率。
这样,我们很容易得到序列位置i+1 的标记是 时,在位置 i+1之前的部分标记序列的非规范化概率 的递推公式:
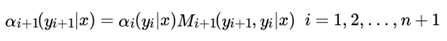
在起点处,我们定义:
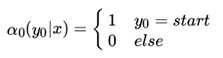
假设我们可能的标记总数是m , 则yi 的取值就有m个,我们用 表示这m个值组成的前向向量如下:
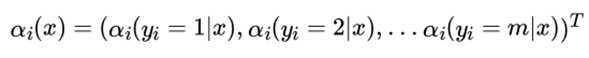
同时用矩阵Mi(x) 表示由Mi(yi−1, yi|x) 形成的 m × m 阶矩阵:
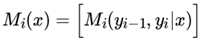
这样递推公式可以用矩阵乘积表示:
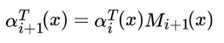
同样的。我们定义βi(yi|x) 表示序列位置 i 的标记是yi 时,在位置 i 之后的从 i+1 到 n 的部分标记序列的非规范化概率。
这样,我们很容易得到序列位置 i+1 的标记是 y_{i+1} 时,在位置 i之后的部分标记序列的非规范化概率 βi(yi|x)的递推公式:
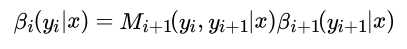
在终点处,我们定义:
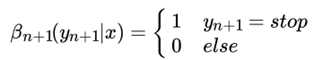
如果用向量表示,则有
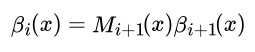
由于规范化因子Z(x) 的表达式是:
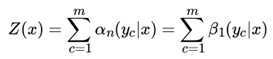
也可以用向量来表示 Z(x):
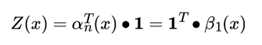
其中, 1是 m 维全1向量。
有了前向后向概率的定义和计算方法,我们就很容易计算序列位置i 的标记是y_i 时的条件概率 P(yi|x):
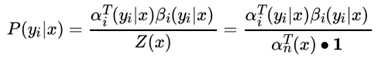
也容易计算序列位置 i的标记是yi ,位置 i+1 的标记是 时的条件概率 P(yi−1, yi|x) :
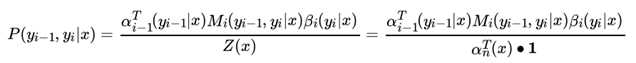
注意到我们上面的非规范化概率 Mi(yi-1, yi|x)起的作用和HMM中的隐藏状态转移概率很像。但是这儿的概率是非规范化的,也就是不强制要求所有的状态的概率和为1。而HMM中的隐藏状态转移概率也规范化的。从这一点看,linear-CRF对序列状态转移的处理要比HMM灵活。
有了上一节计算的条件概率,我们也可以很方便的计算联合分布 P (x, y) 与条件分布 P (y|x)的期望
特征函数 fk(x, y) 关于条件分布 P (y|x) 的期望表达式是:
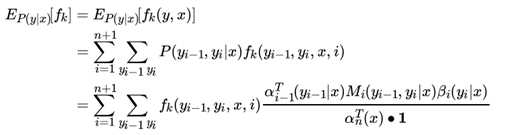
同样可以计算联合分布 P (x, y) 的期望:
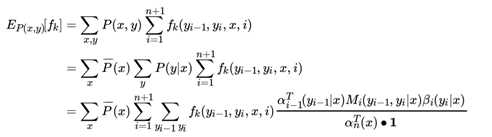
假设一共有 K个特征函数,则 k = 1, 2, . . . K
linear-CRF第二个问题是学习(Learning),即给定训练数据集X和Y,学习linear-CRF的模型参数wk和条件概率Pw(y|x),这个问题的求解比HMM的学习算法简单的多,普通的梯度下降法,拟牛顿法都可以解决。
在linear-CRF模型参数学习问题中,我们给定训练数据集X 和对应的标记序列 Y, K个特征函数 ,【这里是特征函数的规则,可以举个小例子,fk(y2=名词,y3=动词,X,3)=1或0】需要学习linear-CRF的模型参数概率 ,其中条件概率 和模型参数 满足一下关系:
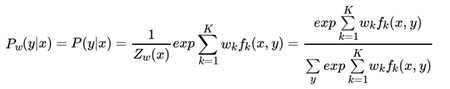
所以我们的目标就是求出所有的模型参数 ,这样条件概率 可以从上式计算出来。
求解这个问题有很多思路,比如梯度下降法,牛顿法,拟牛顿法。同时,这个模型中 的表达式,也可以使用最大熵模型中使用的改进的迭代尺度法(improved iterative scaling, IIS)来求解。
下面我们只简要介绍用梯度下降法的求解思路。
在使用梯度下降法求解模型参数之前,我们需要定义我们的优化函数,一般极大化条件分布 的对数似然函数如下
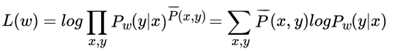
为经验分布,可以从先验知识和训练集样本中得到,这点和最大熵模型类似。为了使用梯度下降法,我们现在极小化如下:
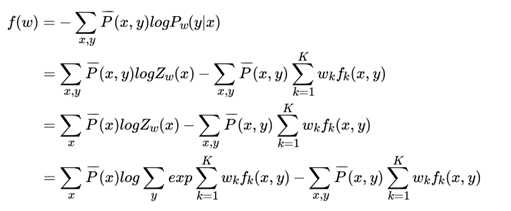
对 W求导可以得到:
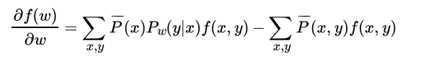
有了W 的导数表达书,就可以用梯度下降法来迭代求解最优的 W了。注意在迭代过程中,每次更新W 后,需要同步更新 ,以用于下一次迭代的梯度计算 。
(PS:实际的使用中,梯度上升法收敛速度太慢,我们会采用其他的计算方式,这里仅做理论指引了)。
linear-CRF第三个问题是解码(Decoding),即给定 linear-CRF的条件概率分布P(y|x),和输入观察序列x, 计算使条件概率最大的输出序列y。类似于HMM,使用维特比算法可以很方便的解决这个问题。
这个解码算法最常用的还是和HMM解码类似的维特比算法。HMM维特比算法解码隐藏状态序列中用于HMM解码。这里也同样采用这种方法。
维特比算法本身是一个动态规划算法,利用了两个局部状态和对应的递推公式,从局部递推到整体,进而得解。对于具体不同的问题,仅仅是这两个局部状态的定义和对应的递推公式不同而已。由于在之前已详述维特比算法,这里就是做一个简略的流程描述。
对于linear-CRF中的维特比算法,我们的第一个局部状态定义为 ,表示在位置 i标记 l 各个可能取值(1,2...m)对应的非规范化概率的最大值。之所以用非规范化概率是,规范化因子 Z(x)不影响最大值的比较。根据 的定义,我们递推在位置i+1 标记 l 的表达式为:
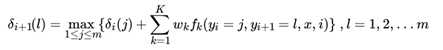
和HMM的维特比算法类似,我们需要用另一个局部状态来记录使达到最大的位置 i 的标记取值,这个值用来最终回溯最优解, 的递推表达式为:
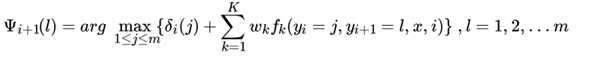
现在我们总结下 linear-CRF模型维特比算法流程:
输入:模型的 K个特征函数,和对应的K个权重。观测序列x = (x1, x2, . . . xn) ,可能的标记个数m
输出:最优标记序列y∗ = (y1∗, y2∗, . . . yn∗)
1) 初始化:
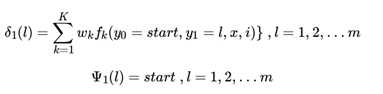
2) 对于i = 1, 2...n − 1 ,进行递推:
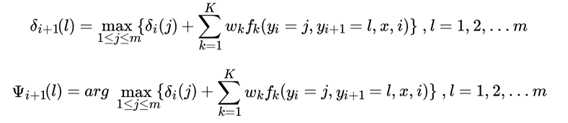
3) 终止:
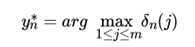
4)回溯:
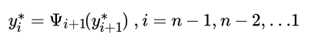
最终得到最优标记序列
下面用一个具体的例子来描述 linear-CRF模型维特比算法:
例子的模型和CRF系列【ML-13-5】中一样,都来源于《统计学习方法》。假设输入的都是三个词的句子,即X = (X1, X2, X3) ,输出的词性标记为Y = (Y1, Y2, Y3) Y ∈ {1(名词),2(动词)} ,其中这里只标记出取值为1的特征函数如下:
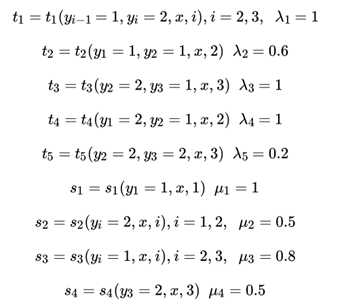
求标记(1,2,2)--【这里式观测序列x】的最可能的标记序列。
求解:
首先初始化( ,表示在位置来记录使达到最大的位置 i 的标记取值):
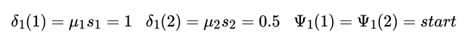
接下来开始递推,先看位置2的:
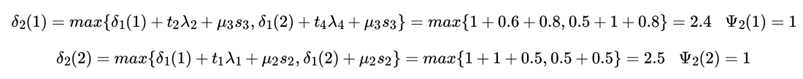
【说明:以,它在序列位置2的取值为1, 那么此时有两种情况,即:a) 它在位置1的取值为1,b)它在位置1的取值为2。a的情况:在位置1的取值为1, 那么对应y1=1,y2=1, 最终可以命中的特征函数是:
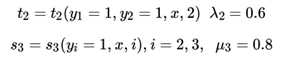
因此a)情况下,它的取值是δ1(1)+t2λ2+μ3s3
同理可以得到b)情况下取值是δ1(2)+t4λ4+μ3s3
最终找到a)和b)的最大值作为δ2(1)的值。 】
再看位置3的:
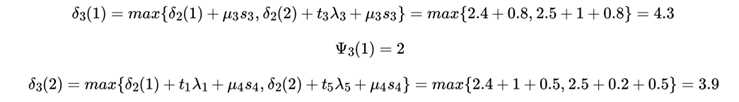
最终得到,递推回去,得到:
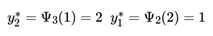
即最终的结果为(1, 2, 1) ,即标记为(名词,动词,名词)。
【1】刘建平博客:https://www.cnblogs.com/pinard/p/7055072.html#!comments
【2】刘建平博客:https://www.cnblogs.com/pinard/p/7068574.html#!comments
【ML-13-6】条件随机场的三个问题(CRF-Conditional Random Field)
标签:取值 coding 强制 影响 nal mic 规划 输入 说明
原文地址:https://www.cnblogs.com/yifanrensheng/p/13193755.html