标签:wap 就是 stream 需要 逆时针 png alt const play
给出一个\(n\)次多项式\(F(x)\),和一个\(m\)次多项式\(G(x)\)
求出$F(x) \(和\)G(x)$的卷积
void solve(){
for(int i = 0; i <= n; i++)
for(int j = 0; j <= m; j++)
c[i + j] += a[i] * b[j];
}
\(f(x) = \{a_0,a_1,a_2,\dots ,a_{n - 1}\}\)
把多项式放到平面直角坐标系里,看成一个函数
把\(n\)个不同的\(x\)带入,得到唯一确定的\(y\),就有\(n\)个不同的点
\(f(x) = \{(x_0,f(x_0)), (x_1,f(x_1)),\dots, (x_{n - 1}, f(x_{n - 1}))\}\)
设\(f(x) = \{(x_0,f(x_0)), (x_1,f(x_1)),\dots , (x_{n},f(x_{n}))\}\)
设\(g(x) = \{(x_0,f(x_0)),(x_1,f(x_1)),\dots,(x_{n},f(x_n))\}\)
那么\(f(x)g(x) = \{(x_0,f(x_0)?g(x_0)),(x_1,f(x_1)?g(x_1)),\dots,(x_n,f(x_n)?g(x_n))\}\)
设\(z_1 = a + bi, z_2 = c + di\)
考虑将一个\(n\)项\((n = 2^k)\)的多项式\(A(x)\),将其系数表达式转换为点值表达式,求出每一个点值的过程
把一个单位圆进行n等分,编号为从0开始逆时针编号
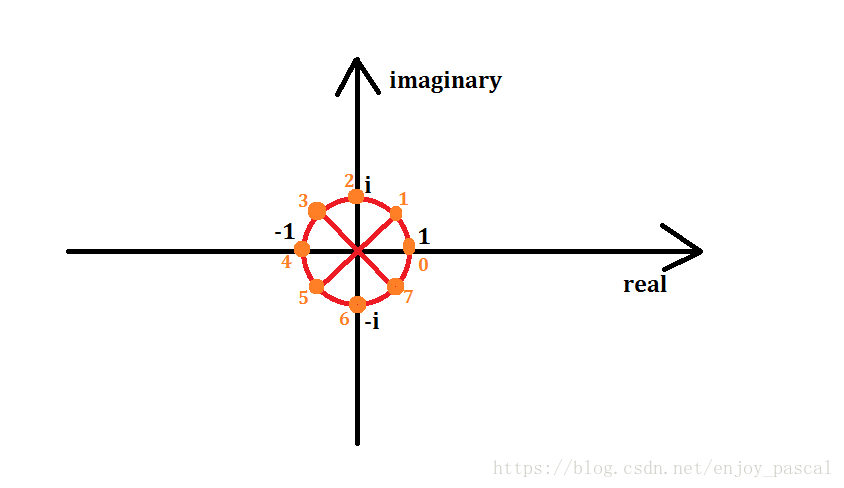
记编号为\(k\)的点代表的复数值为\(w_n^k\),因为模长相同,极角相加可知\((\omega_n^1)^k = \omega_n^k\)
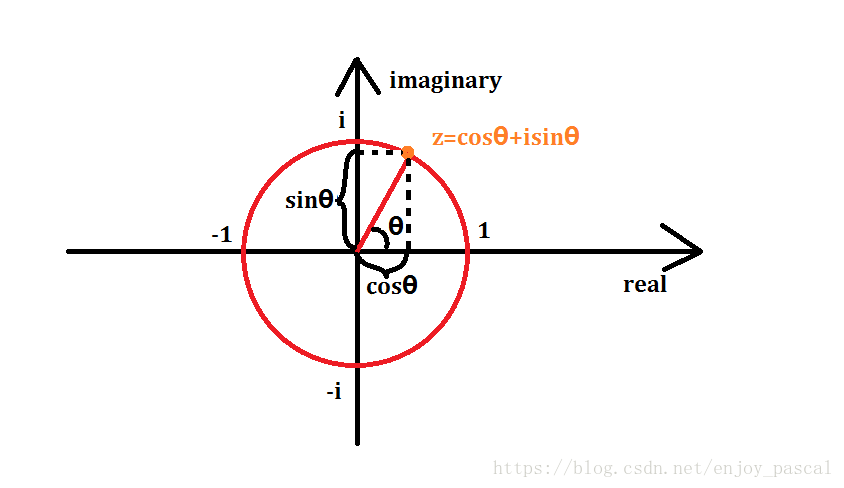
那么\(\omega_n^0,\omega_n^1,\dots, \omega_n^{n-1}\)就是要带入的\(x_0,x_1,\dots ,x_{n - 1}\)
利用DFT来分治求
对于一个多项式\(A(x) = \sum_{i = 0}^{n - 1}a_ix^i\)
按照\(A(x)\)下标的奇偶性把\(A(x)\)分成两半
设多项式\(A_1(x),A_2(x)\)
满足\(A(x) = A_1(x^2) + xA_2(x^2)\)
设\(k < \frac{n}{2}\),把\(\omega_n^k\)作为\(x\)带入\(A(x)\)
那么对于那对于\(k ≥\frac{n}{2}\)的情况,令$k = \frac{n}{2} + k, k<\frac{k}{2} \(即\)A(\omega_n^{k + \frac{n}{2}})$,有
发现\(A(\omega_n^k)\)和\(A(\omega_n^{k + \frac{n}{2}})\)两个多项式只有后面的符号不同
也就是说,如果知道了\(A_1(\omega_{\frac{n}{2}}^k)\)和\(A_2(\omega_{\frac{n}{2}}^k)\),就可以同时知道\(A(\omega_n^k)\)和\(A(\omega_n^{k + \frac{n}{2}})\)
那么就可以递归分治来求得每一个\(A(x)\)
时间复杂度\(O(nlogn)\)
利用快速傅里叶变换将点值表达式的多项式转换为系数表示的过程
把DFT的\(\omega_n\)都取复数(共轭复数),最后除以\(n\)即可
#include <iostream>
#include <cstdio>
#include <complex>
using namespace std;
const double Pi = acos(-1);
const int N = 4e6 + 5;
complex<double> f[N], g[N];
void FFT(complex<double> *a, int n, int inv){
if(n == 1)return;
complex<double> a1[n >> 1], a2[n >> 1];
for(int i = 0; i < n ; i += 2)
a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
FFT(a1, n >> 1, inv); FFT(a2, n >> 1, inv);
complex<double> x(cos(2 * Pi / n), sin(2 * Pi / n) * inv), w(1, 0);
for(int i = 0; i < (n >> 1); i++, w *= x)
a[i] = a1[i] + w * a2[i], a[i + (n >> 1)] = a1[i] - w * a2[i];
}
int main(){
int n, m, x;
scanf("%d%d", &n, &m);
for(int i = 0; i <= n; i++){
scanf("%d", &x), f[i].real(x);
}
for(int i = 0; i <= m; i++){
scanf("%d", &x), g[i].real(x);
}
for(m += n, n = 1; n <= m; n <<= 1);
FFT(f, n, 1); FFT(g, n, 1);
for(int i = 0; i < n; i++)
f[i] *= g[i];
FFT(f, n, -1);
for(int i = 0; i <= m; i++)
printf("%d ", int(0.5 + f[i].real() / n));
return 0;
}
发现递归版每次都需要开辟一个数组,而且值还需要重新赋值

假设数组\(a\)已经变成了第四层,那么先对\(a_0\)和\(a_4\),\(a_4\)和\(a_2\),\(a_2\)和\(a_6\),\(a_6\)和\(a_1\),\(a_1\)和\(a_5\),\(a_5\)和\(a_3\),\(a_3\)和\(a_7\)进行蝴蝶操作,变成第三层,依次类推
那么问题就是把初始化数组变成最后一层,
考虑二进制形式000,100,010,110,001,101,011,111和原数组000,001,010,011,100,101,110,111就是二进制的每个位置的反过来
#include <cstdio>
#include <iostream>
#include <complex>
#include <cmath>
using namespace std;
const int N = 3e6 + 1;
const double Pi = acos(-1);
int n, m, r[N];
complex<double> F[N], G[N];
int getint() {
int x = 0, f = 1; char c = getchar();
while(c < ‘0‘ || c > ‘9‘) {if(c == ‘-‘) f = -1; c = getchar();}
while(c >= ‘0‘ && c <= ‘9‘) x = (x << 1) + (x << 3) + c - ‘0‘, c = getchar();
return x * f;
}
void FFT(complex<double> *a, int n, int inv){
for(int i = 0; i < n; i++)
if(r[i] > i) swap(a[r[i]], a[i]);
for(int mid = 2; mid <= n; mid <<= 1){
complex<double> x(cos(2 * Pi / mid), inv * sin(2 * Pi / mid));
for(int i = 0; i < n; i += mid){
complex<double> w(1,0);
for(int j = i; j < i + (mid >> 1); j++, w *= x){
complex<double> t1 = a[j],t2 = a[j + (mid >> 1)] * w;
a[j] = t1 + t2; a[j + (mid >> 1)] = t1 - t2;
}
}
}
}
int main(){
scanf("%d %d", &n, &m);
for(int i = 0; i <= n; i++) F[i].real(getint());
for(int i = 0; i <= m; i++) G[i].real(getint());
int l = 0;
for(m += n, n = 1; n <= m; n *= 2, l++);
for(int i = 0; i < n; i++)
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
FFT(F, n, 1); FFT(G, n, 1);
for(int i = 0; i < n; i++) F[i] = F[i] * G[i];
FFT(F, n, -1);
for(int i = 0; i <= m; i++)
printf("%d ", (int)(F[i].real() / n + 0.5));
return 0;
}
看成一个多项式\(a_0 + a_1 \times 10 + a_2 \times 10^2 + \dots +a_{n}\times 10^n\)
#include <cstdio>
#include <iostream>
#include <complex>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e6 + 1;
const double Pi = acos(-1);
int n, m, r[N];
complex<double> F[N], G[N];
void FFT(complex<double> *a, int n, int inv){
for(int i = 0; i < n; i++)
if(r[i] > i) swap(a[r[i]], a[i]);
for(int mid = 2; mid <= n; mid <<= 1){
complex<double> x(cos(2 * Pi / mid), inv * sin(2 * Pi / mid));
for(int i = 0; i < n; i += mid){
complex<double> w(1,0);
for(int j = i; j < i + (mid >> 1); j++, w *= x){
complex<double> t1 = a[j],t2 = a[j + (mid >> 1)] * w;
a[j] = t1 + t2; a[j + (mid >> 1)] = t1 - t2;
}
}
}
}
void solve(){
int l = 0;
for(m += n, n = 1; n <= m; n *= 2, l++);
for(int i = 0; i < n; i++)
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
FFT(F, n, 1); FFT(G, n, 1);
for(int i = 0; i < n; i++)F[i] = F[i] * G[i];
FFT(F, n, -1);
int dig = 0;
char s[N];
for(int i = 0; i <= m; i++){
int x = (int)(F[i].real() / n + 0.5) + dig;
dig = x / 10; x %= 10;
s[i] = ‘0‘ + x;
}
while(dig){
s[++m] = dig % 10 + ‘0‘;
dig /= 10;
}
s[++m] = ‘\0‘;
reverse(s, s + m);
printf("%s\n", s);
}
int main(){
char s[N];
scanf("%s", s);
n = strlen(s) - 1;
for(int i = 0; i <= n; i++)F[i].real(s[n - i] - ‘0‘);
scanf("%s", s);
m = strlen(s) - 1;
for(int i = 0; i <= m; i++)G[i].real(s[m - i] - ‘0‘);
solve();
return 0;
}
标签:wap 就是 stream 需要 逆时针 png alt const play
原文地址:https://www.cnblogs.com/Emcikem/p/13194161.html