标签:include 最大 最小 cout star 问题 pop 假设 基于邻接表
一、第六章内容小结
本章内容思维导图
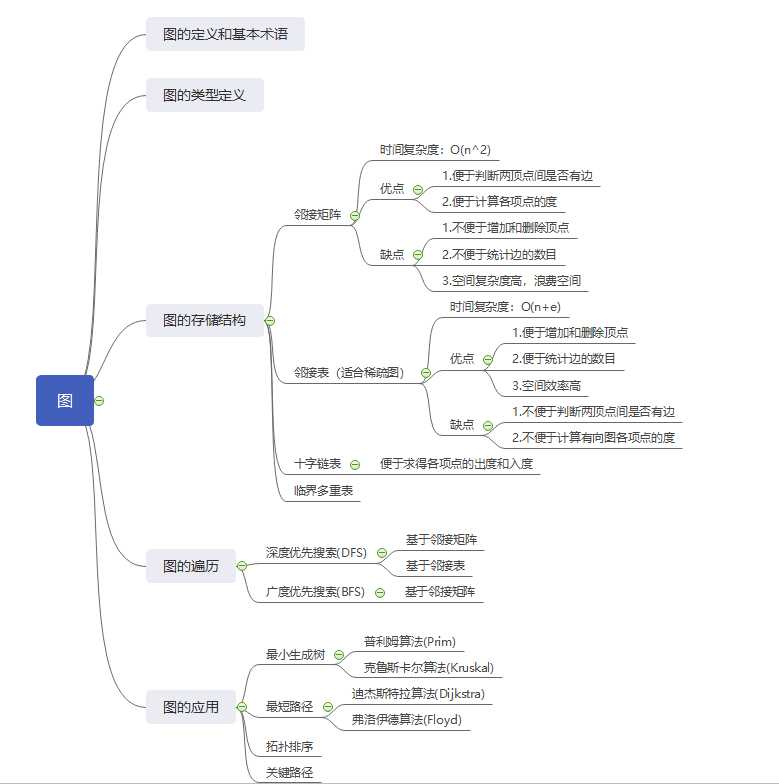
1. 邻接矩阵储存
1 #define MVNum 100 //最大顶点数 2 typedef char VerTexType;//假设顶点的数据类型为字符型 3 typedef int ArcType;//假设边的权值类型为整型 4
5 typedef struct 6 { 7 VerTexType vexs [MVNum] ;//顶点表 8 ArcType arcs[MVNum][MVNum];//邻接矩阵 9 int vexnum, arcnum;//图的当前总顶点数和总边数 10 }AMGraph;
2. 邻接表储存
1 #define MVNum 100//最大顶点数 2 typedef char VerTexType;//假设顶点的数据类型为字符型 3 typedef int ArcType;//假设边的权值类型为整型 4 5 typedef struct ArcNode//边结点 6 { 7 int adjvex;//邻接点的位置 8 struct ArcNode *nextarc;//指向下一条边的指针 9 Otherinfo info;///和边相关的信息 10 }ArcNode; 11 12 typedef struct VNode//顶点 13 { 14 VerTexType data; 15 ArcNode *firstarc;//指向第一条依附该顶点的边的指针 16 }VNode,AdjList[MVNum];//AdjList表示邻接表类型 17 18 typedef struct//邻接表 19 { 20 AdjList vertices;//存储顶点信息的数组 21 int vexnum,arcnum;//图的当前总顶点数和总边数 22 }ALGraph;
3. 深度优先搜索(DFS)
①基于邻接矩阵
1 void DFS( Graph g,int v,int visited[]) 2 { 3 /* 邻接矩阵存储,从顶点v出发,对图g进行深度优先搜索*/ 4 int j; 5 cout << g.vexs[v]; 6 visited[v]=1; /*标识v被访问过*/ 7 for(j=0;j<g.vexnum;j++); /* */ 8 { 9 if( g.arcs[v][j]==1&&visited[j]==0)/*j为v的邻接点,未被访问过*/ 10 DFS(g,j,visited); /*从j出发递归调用DFS*/ 11 }/*for*/ 12 }/*DFS*/ 13 14 void DFSTraverse(Graph g) 15 { 16 /*邻接矩阵 深度优先搜索*/ 17 int v; 18 int visited[MVNUM]; 19 for(v=0;v<g.vexnum;v++) 20 visited[v]=0; /*初始化visited数组*/ 21 for(v=0;v<g.vexnum;v++) 22 if(visited[v]==0) 23 DFS(g,v,visited); 24 /*从未被访问过的v出发, DFS搜索*/ 25 }
②基于邻接表
1 void DFS(ALGraph g,int v,int visited[]) 2 { 3 /*从顶点v出发,对图g进行深度优先搜索*/ 4 ArcNode *p; 5 int w; 6 cout << g.adjlist[v].data; 7 visited[v]=1; /*标识v被访问过*/ 8 p=g.adjlist[v].firstarc; /*p指向第v个单链表的头指针*/ 9 while(p) 10 { 11 w=p->adjvex; /*w为v的邻接点*/ 12 if(visited[w]==0) /*若w未被访问*/ 13 DFS(g,w,visited); /*从w出发递归调用DFS*/ 14 p=p->nextarc; /*找v的下一个邻接点*/ 15 }/*while*/ 16 }/*DFS*/ 17 18 void DFSTraverse(ALGraph g) 19 { 20 /*邻接表 深度优先搜索*/ 21 int v; 22 int visited[MAX_VERTEX_NUM]; 23 for(v=0;v<g.vexnum;v++) 24 visited[v]=0; /*初始化visited数组*/ 25 for(v=0;v<g.vexnum;v++) 26 if(visited[v]==0) 27 DFS(g,v,visited); 28 /*从未被访问过的v出发, DFS搜索*/ 29 }
4. 广度优先搜索(BFS)
①基于邻接矩阵
1 /*采用邻接矩阵表示图的广度优先遍历*/ 2 void BFS_AM(AMGraph &G,char v0) 3 { 4 /*从v0元素开始访问图*/ 5 6 int u,i,v,w; 7 v = LocateVex(G,v0); //找到v0对应的下标 8 cout << v0; //打印v0 9 visited[v] = 1; //顶点v0已被访问 10 q.push(v0); //将v0入队 11 12 while (!q.empty()) 13 { 14 u = q.front(); //将队头元素u出队,开始访问u的所有邻接点 15 v = LocateVex(G, u); //得到顶点u的对应下标 16 q.pop(); //将顶点u出队 17 for (i = 0; i < G.vexnum; i++) 18 { 19 w = G.vexs[i]; 20 if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问 21 { 22 cout << w; //打印顶点w 23 q.push(w); //将顶点w入队 24 visited[i] = 1; //顶点w已被访问 25 } 26 } 27 } 28 }
②基于邻接表
1 #include<queue> 2 void BFS(Graph G, int v) 3 { 4 visited[v] = true;//访问过的顶点置为true 5 6 queue<int> q;//辅助队列Q初始化 7 q.push(v);//v进队 8 9 while(!q.empty())//队列非空 10 { 11 int u = q.front();//队头元素出队并置为u 12 q.pop(); 13 p = G.vertices[u].firstarc;//p指向u的第一个边结点 14 while(p != NULL) //边结点非空 15 { 16 w = p->adjvex; 17 if(!visited[w])//若w未访问 18 { 19 visited[w] = true; 20 q.push(w)//w进队 21 } 22 p = p->nextarc; //p指向下一个边结点 23 } 24 } 25 }
5. Prim / Kruskal / Dijkstra / Floyd 算法
普里姆(Prim)算法:
1. 找出最短的边
2. 以这条边构成的整体去寻找与之相邻的边,直至连接所有顶点,生成最小生成树。
克鲁斯卡尔(Kruskal)算法:
1. 从任意一条单边路径开始。所有两点之间的距离是边的权,或者无穷大,如果两点之间没有边相连。
2. 对于每一对顶点u和v,看看是否存在一个顶点w使得从u到w再到v比己知的路径更短。如果是更新它。
二、学习总结
这一章节主要学习了图的存储结构、遍历和多种算法等。存储结构、图的遍历在理解上没有什么大的问题,但是算法概念比较多,容易混淆,且如果不看书用代码复现的话还是有难度。
标签:include 最大 最小 cout star 问题 pop 假设 基于邻接表
原文地址:https://www.cnblogs.com/cbs-2397812053/p/13195180.html